SGU 204. Little Jumper

204. Little Jumper

time limit per test: 0.5 sec.
memory limit per test: 65536 KB
input: standard
output: standard

Little frog Georgie likes to jump. Recently he have discovered the new playground that seems the perfect place to jump.

Recently the new jumping exercise has become very popular. Two vertical walls are placed on the playground, each of which has a hole.

The lower sides of the holes in the walls are on heights b1 and b2 respectively, and upper sides on heights t1 and t2. Walls are parallel and placed on distance l from each other.

The jumper starts at the distance ds from the first wall. It jumps through the first hole and lands between the walls. After that from that point he jumps through the second hole. The goal is to land exactly at the distance df from the second wall.

Let us describe the jump. The jumper starts from the specified point and starts moving in some chosen direction with the speed not exceeding some maximal speed v, determined by the strength of the jumper. The gravity of g forces him down, thus he moves along the parabolic trajectory.

The jumper can choose different starting speeds and different directions for his first and second jump.

Of course, The jumper must not attempt to pass through the wall, although it is allowed to touch it passing through the hole, this does not change the trajectory of the jump. The jumper is not allowed to pass through both holes in a single jump.

Find out, what must be the maximal starting speed of the jumper so that he could fulfil the excersise.

Input

Input file contains one or more lines, each of which contains eight real numbers, separated by spaces and/or line feeds. They designate b1, t1, b2, t2, l, ds, df and g. All numbers are in range from 10-2 to 103, t1≥ b1 + 10-2, t2≥ b2 + 10-2.

Output

For each line of the input file output the smallest possible maximal speed the jumper must have to fulfil the exercise. If it is impossible to fulfil it, output -1. Your answer must be accurate up to 10-4.

Sample test(s)

Input

0.3 1.0 0.5 0.9 1.7 1.2 2.3 9.8
0.6 0.8 0.6 0.8 2.4 0.3 1.5 0.7

Output

5.2883
1.3127

---

附送中文题意

题意

有只小青蛙要从两个竖起来的间隔为\(l\)的，各自有两个洞，分别以上部离地高度和下部离地高度描述，\(t_1,\ b_1,\ t_2,\ b_2\)的隔板跳过去。要求跳两次，一次从离第一块隔板\(d_s\)距离处以初速度\(v_1\)，方向自定，跳进隔板间，落脚点自定，一次以速度\(v_2\)，方向自定，从另外一边跳出来落在离第二块隔板\(d_t\)处，要你求最小的速度，即\(\min(\ max(\ v_1,\ \ v_2\ )\ )\)。

参见此图：


考虑一次跳跃，从\((0,\ 0)\)跳到\((x_2,\ 0)\)，以高度\(y_1\)越过在\(x_1\)处的障碍，求最小速度\(v\)。

设x方向上的速度为\(v_x\)，y为\(v_y\)，那么高y和远x成方程。设时间$t=\frac{x}{v_x} \(，那么\)y = \frac{v_y + v_y - t \times g}{2}\times t=t\times v_y - \frac{t^2}{2}\times g=\frac{x\times v_y}{v_x} - \frac{x^2\times g}{2\times v_x^2}\(；
用\)v_x, v_y$表示得：

\[2y\times v_x^2 - 2x\times v_y\times v_x + x^2g=0
\]

对于两组点：\((x_1,y_1)\)，\((x_2,y_2)\)，可以通过解方程得出\((v_x,v_y)\)，那么初始速度即为\(\sqrt{v_x^2+v_y^2}\)。

\[v_y^2=\frac{(2y_1\times v_x^2+x_1^2g)^2}{(2x_1\times v_x)^2}
\]

\[v_x^2=\frac{x_1^2x_2g-x_1x_2^2g}{2y_2x_1-2y_1x_2}
\]

然后没了。。

notice

1. 如果出射角为45度为最优，但是考虑到“洞”的限制，发现，如果45度可以通过，则取45度作为出射角，否则如果45度的抛物线交于洞顶上方时，取通过上方端点的点在抛物线上，否则取下方点，见下图（引用自Vergissmeinnicht）：
   
   

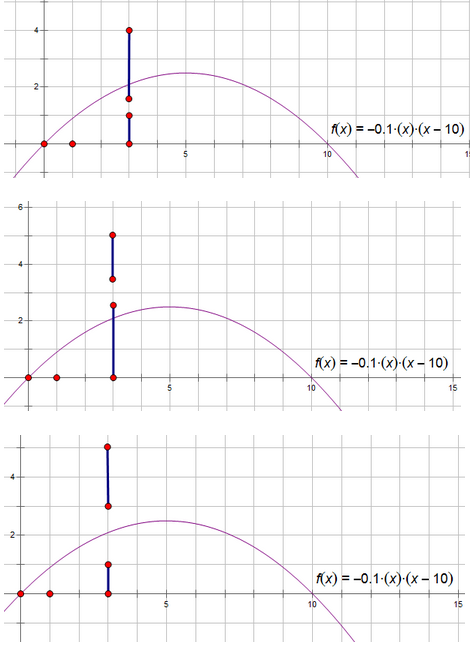
2. 其他没啥了。。。1A的。。

#include <cstdio>
#include <cstring>
#include <cmath>
#define max(x, y) ((x) < (y) ? (y) : (x))
typedef double DB;
const DB eps = 1e-12;

DB ds, df, t1, t2, b1, b2, dist, g;
#define sqr(x) ((x) * (x))
DB calc(DB s, DB y2, DB y1, DB x1, DB x2) {
	DB jud = x1 - x1 * x1 / x2;
	if(y1 <= jud && jud <= y2) return x2 * g;
	if(jud < y1) {
		y2 = 0.0;
	} else {
		y1 = y2;
		y2 = 0.0;
	}
	DB vx2 = (sqr(x1) * x2 * g - x1 * sqr(x2) * g) / 2 / (x1 * y2 - x2 * y1);
	DB vy2 = (sqr(2 * y1 * vx2 + sqr(x1) * g) / vx2 / sqr(x1) / 4);
	//printf("%lf %lf\n", vx2, vy2);
	return vx2 + vy2;
}

DB calc(DB pos) {
	return max(calc(0.0, t1, b1, ds, pos + ds), calc(0.0, t2, b2, dist - pos, dist - pos + df));
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("204.in", "r", stdin);
	freopen("204.out", "w", stdout);
#endif
	while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &b1, &t1, &b2, &t2, &dist, &ds, &df, &g) != EOF) {
		DB l = 0, r = dist;
		while(eps < r - l) {
			DB m1, m2;
			m1 = l + (r - l) / 3;
			m2 = l + (r - l) / 3 * 2;
			DB a1, a2;
			a1 = calc(m1);
			a2 = calc(m2);
			if(a1 < a2) r = m2;
			else l = m1;
		}
		DB ans = sqrt(calc((l + r) / 2));
		printf("%.4lf\n", ans);
	}
	return 0;
}