retrival and clustering : week 4 GMM & EM 笔记

华盛顿大学 机器学习 笔记。

k-means的局限性

　　k-means 是一种硬分类（hard assignment）方法，例如对于文档分类问题，k-means会精确地指定某一文档归类到某一个主题，但很多时候硬分类并不能完全描述这个文档的性质，这个文档的主题是混合的，这时候需要软分类（soft assignment）模型。

　　k-means 缺陷：（1）只关注聚类中心的表现。（2）聚类区域形状必须为对称圆形／球形，轴平行。

　　对于聚类区域大小不一、轴不平行、聚类空间重叠等情况，k-means 缺陷显著。
　　　　　　　　

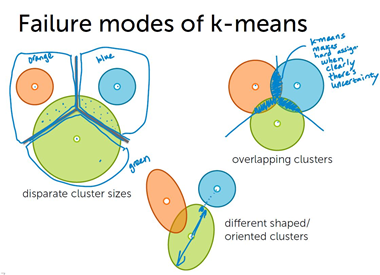
混合模型的优点：

　　1.软分类（例如，主题 54%“世界新闻”，45% “科学”， 1% “体育”）

　　2.关注聚类区域形状而不只是中心

　　3.每个聚类的权重（weights）可学习

高斯混合模型(GMM)

(1) 高斯函数描述聚类分布

　　高斯混合模型假定每个聚类可以用一个高斯分布函数N(x|μ ,Σ)描述，如图

　　　　　　　　

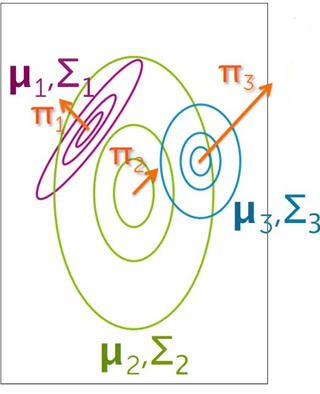
　　描述聚类的参数有三个， { π, μ , Σ }，其中，π 为聚类 的权重（weight），μ为 聚类的平均值（mean），Σ 为聚类的协方差（covariance）.

　　高斯混合模型概率分布:

　　　　　　

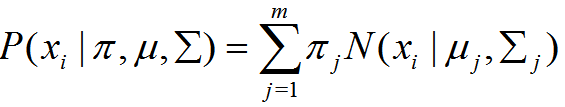
　　如何理这个解概率分布模型，以计算点xi属于聚类k的概率为例。

（2）如何计算点 xi 属于聚类k 的概率？

　　　贝叶斯公式：

　　　　　　　　　

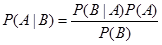
　　　　假设从数据集中随机抽取一个数据点，考虑以下几种情况：

　　　　　　　　A  = 抽到的点属于聚类k

　　　　　　　　B  = 抽到点xi

　　　　　　　　B|A = 已知抽取的点属于聚类k 中, 抽到点xi

　　　　　　　　A|B = 已知抽到点xi, 抽取的点属于聚类k

　　　　　P(A|B)其实等价于”点xi属于聚类k”的概率。

　　　　接下来求P(A)、P(B)、P(B|A)，通过贝叶斯公式可求P(A|B)。

　　　　

　　A  = 抽到的点属于聚类k

　　P(A)：从数据集中随机抽取一个点，恰好抽到聚类k中的点的概率。

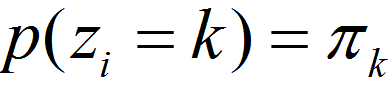　　　　  （其中，所有聚类权重之和为1，即 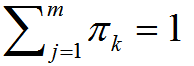，m为聚类数量)

　　　即

　　　　　　　　　　　　

　

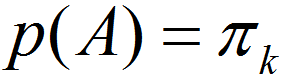
　　B|A = 已知抽取的点属于聚类k,中, 抽到点xi

　   P(B|A)：转换为从聚类k中随机抽一个点，恰好抽到点xi的概率。

　　GMM模型假设每个聚类中数据点服从高斯分布：

　　　　　　

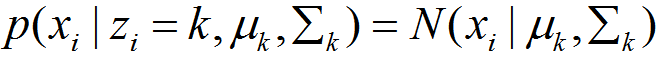
　　即

　　　　　　

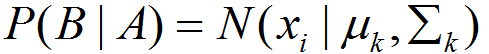
    　B  = 抽到点xi

　　P(B)：从数据集中随机抽取一个点，恰好抽到点xi的概率。

　　这种情况下，抽到的点归属于哪个/些聚类未知，考虑到：

　　　　　如果已知抽到的点属于哪些聚类，这个概率可以按照P(B|A)的公式算。

　　　　　从数据集中随机抽点，抽到的点属于某个聚类的概率，可以按照P(A)的公式计算。

　　 使用用条件概率公式计算：

　　　　

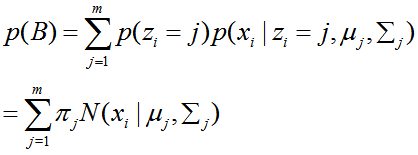
　　这就是就是GMM模型的概率分布模型。

　　点xi属于聚类k的概率，即后验概率为：

　　　　

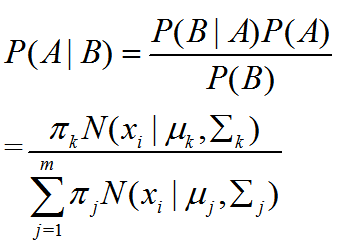
　　即

　　　

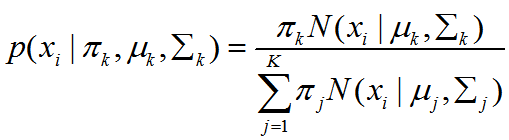
（3）评估GMM模型优劣的方法——似然性

　　首先明确隐变量：

　　假设整个数据集是从符合这个GMM模型的大样本中随机抽取点构成的，每次抽取的数据记为 xi（i = 1,2,…,N， 数据集中一共N个点）,对于第i次抽取的点，此时xi是已知的，而 xi属于哪个聚类未知，以隐变量γ表示，其中

　　　　　　

　　γ为随机变量。则变量的完全数据为

　　　　 

　　

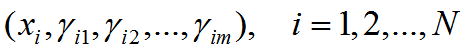
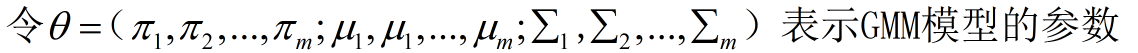
　　似然函数表示的是，在当前GMM模型的参数下，以上述方法形成的数据集，恰好构成了原本的数据集的概率。

　　似然函数计算式：

　　　　　　

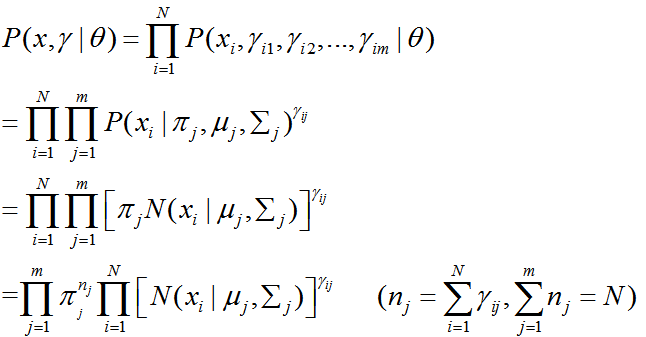
　　其中多维高斯分布函数（维数为dim）：

　　　　

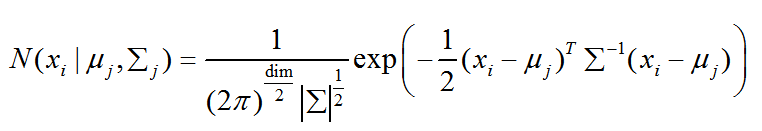
　　实际应用中常常使用对数似然函数：

　　　　

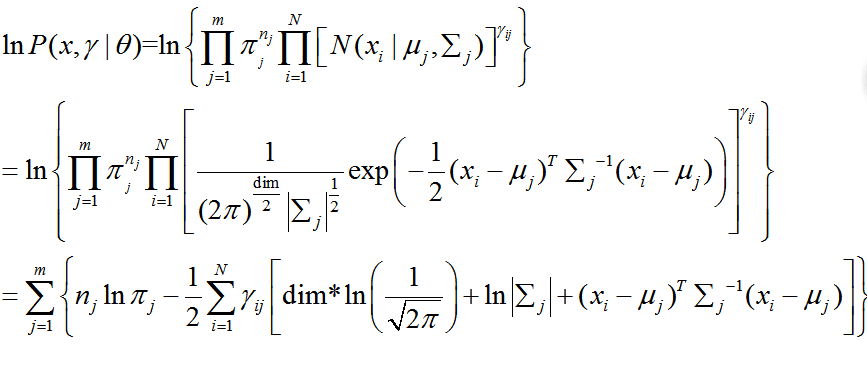
EM算法

　　EM算法（expectation maximization, 期望最大化），计算GMM模型分两步：

　　　　　　1. E- step： 根据当前GMM模型的参数，计算（estimate）对数似然性的期望值。

　　　　　　2. M-step： 求使似然性(likelihood)期望最大的新的模型参数。

E-step：

　　对数似然性表达式：

　　　

　　求期望要先明确一件事，随机变量是什么？

　　　　　　　　隐变量γ

　　即

　　

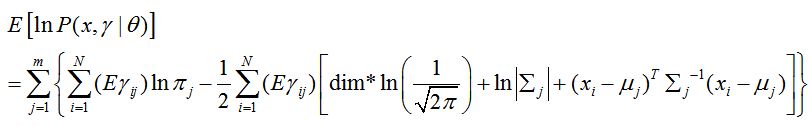
隐变量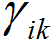的期望称为聚类k对xi的响应度（responsibility）。记为

　　　　　　　　　　

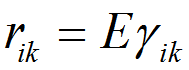
考虑到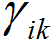表示的意义是，xi是否属于聚类k。因此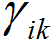的期望就是在当前模型参数下，xi属于聚类k的概率，即

　　　　　　　

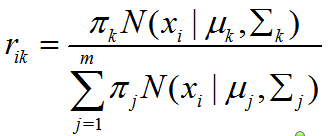
带入原式得：

　　

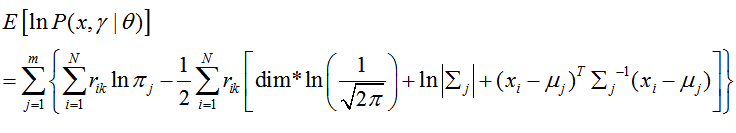
def log_sum_exp(Z):
    """ Compute log(\sum_i exp(Z_i)) for some array Z."""
    return np.max(Z) + np.log(np.sum(np.exp(Z - np.max(Z))))

def loglikelihood(data, weights, means, covs):
    """ Compute the loglikelihood of the data for a Gaussian mixture model. """
    num_clusters = len(means)
    num_dim = len(data[0])
    num_data = len(data)
    resp = compute_responsibilities(data, weights, means, covs)

    log_likelihood = 0
    for k in range(num_clusters):

        Z = np.zeros(num_clusters)
        for i in range(num_data):

            # Compute (x-mu)^T * Sigma^{-1} * (x-mu)
            delta = np.array(data[i]) - means[k]
            exponent_term = np.dot(delta.T, np.dot(np.linalg.inv(covs[k]), delta))

            Z[k] += np.log(weights[k])
            Z[k] -= 1/2. * (num_dim * np.log(2*np.pi) + np.log(np.linalg.det(covs[k])) + exponent_term)
            Z[k] = resp[i][k]* Z[k]

        log_likelihood += log_sum_exp(Z)

    return log_likelihood

M-step:

求使似然性期望最大的新的模型参数。似然性期望的公式：

　　

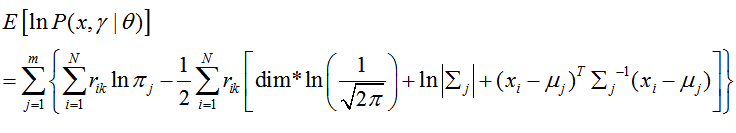
用这个式子分别对 { π, μ , Σ }这几个参数求偏导数，并令偏导数为0，即可得到新的模型参数。

聚类k的新参数计算：

　　　　　　　　　

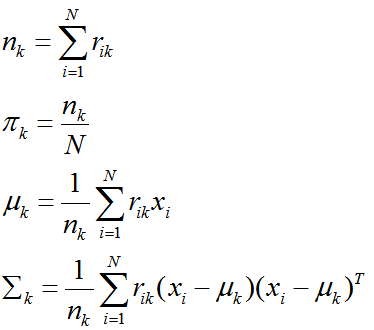
EM是一种 坐标上升(coordinate-ascent)算法，多次迭代直到对数似然函数的值不再有明显变化，得到局部最优解。

def EM(data, init_means, init_covariances, init_weights, maxiter=1000, thresh=1e-4):
    # Initialize
    means = init_means[:]
    covariances = init_covariances[:]
    weights = init_weights[:]
    num_data = len(data)
    num_dim = len(data[0])
    num_clusters = len(means)
    resp = np.zeros((num_data, num_clusters))
    log_likelihood = loglikelihood(data, weights, means, covariances)
    ll_trace = [log_likelihood]

    for it in range(maxiter):
        # E-step:
        resp = compute_responsibilities(data, weights, means, covariances)

        # M-step:
        # 更新 n(k),weight(k),mean(k),covariances(k)
        counts = compute_counts(resp)
        weights = compute_weights(counts)
        means = compute_means(data, resp, counts)
        covariances = compute_covariances(data, resp, counts, means)

        # 计算此次迭代之后的log likelihood
        ll_latest = loglikelihood(data, weights, means, covariances)
        ll_trace.append(ll_latest)

        # 收敛？
        if (ll_latest - log_likelihood) < thresh and ll_latest > -np.inf:
            break
        log_likelihood = ll_latest

    model = {'weights': weights, 'means': means, 'covs': covariances, 'loglik': ll_trace, 'resp': resp}

    return model