A1261. happiness(吴确)[二元组暴力最小割建模]
接下来是六个矩阵
第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。
第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。
第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。
第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。
第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。
第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。
1 1
100 110
1
1000
对于30%以内的数据,n,m<=8
对于100%以内的数据,n,m<=100 数据保证答案在2^30以内
对于100%的数据,时间限制为0.5s。


源代码
- #include<cstdio>
- #include<cstring>
- #include<iostream>
- #define EF if(ch==EOF) return x;
- #define rep for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)
- #define rep1 for(int i=1;i<n;i++)for(int j=1;j<=m;j++)
- #define rep2 for(int i=1;i<=n;i++)for(int j=1;j<m;j++)
- using namespace std;
- const int Z=105;
- const int N=Z*Z;
- const int M=N*30;
- struct edge{int v,next,cap;}e[M<<1];int tot=1,head[N];
- int n,m,cnt,res,ans,S,T,dis[N],q[N+M];
- int a[Z][Z],b[Z][Z],id[Z][Z];
- inline int read(){
- int x=0,f=1;char ch=getchar();
- while(ch<'0'||ch>'9'){if(ch=='-')f=-1;EF;ch=getchar();}
- while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
- return x*f;
- }
- void add(int x,int y,int z){
- e[++tot].v=y;e[tot].cap=z;e[tot].next=head[x];head[x]=tot;
- e[++tot].v=x;e[tot].cap=0;e[tot].next=head[y];head[y]=tot;
- }
- void Add(int x,int y,int z){
- e[++tot].v=y;e[tot].cap=z;e[tot].next=head[x];head[x]=tot;
- e[++tot].v=x;e[tot].cap=z;e[tot].next=head[y];head[y]=tot;
- }
- bool bfs(){
- memset(dis,-1,sizeof dis);
- int h=0,t=1;q[t]=S;dis[S]=0;
- while(h!=t){
- int x=q[++h];
- for(int i=head[x];i;i=e[i].next){
- if(e[i].cap&&dis[e[i].v]==-1){
- dis[e[i].v]=dis[x]+1;
- if(e[i].v==T) return 1;
- q[++t]=e[i].v;
- }
- }
- }
- return 0;
- }
- int dfs(int x,int f){
- if(x==T) return f;
- int used=0,t;
- for(int i=head[x];i;i=e[i].next){
- if(e[i].cap&&dis[e[i].v]==dis[x]+1){
- t=dfs(e[i].v,min(e[i].cap,f));
- e[i].cap-=t;e[i^1].cap+=t;
- used+=t;f-=t;
- if(!f) return used;
- }
- }
- if(!used) dis[x]=-1;
- return used;
- }
- void dinic(){
- res=0;
- while(bfs()) res+=dfs(S,2e9);
- }
- int main(){
- n=read();m=read();
- rep a[i][j]=read();
- rep b[i][j]=read();
- rep id[i][j]=++cnt;
- S=0;T=cnt+1;
- #define u id[i][j]
- #define v id[i+1][j]
- rep{
- add(S,u,b[i][j]<<1);
- add(u,T,a[i][j]<<1);
- ans+=a[i][j]+b[i][j];
- }
- rep1 a[i][j]=read();
- rep1 b[i][j]=read();
- rep1{
- add(S,u,b[i][j]);add(S,v,b[i][j]);
- add(u,T,a[i][j]);add(v,T,a[i][j]);
- Add(u,v,a[i][j]+b[i][j]);
- ans+=a[i][j]+b[i][j];
- }
- #undef v
- #define v id[i][j+1]
- rep2 a[i][j]=read();
- rep2 b[i][j]=read();
- rep2{
- add(S,u,b[i][j]);add(S,v,b[i][j]);
- add(u,T,a[i][j]);add(v,T,a[i][j]);
- Add(u,v,a[i][j]+b[i][j]);
- ans+=a[i][j]+b[i][j];
- }
- dinic();
- res>>=1;
- printf("%d",ans-res);
- return 0;
- }
A1261. happiness(吴确)[二元组暴力最小割建模]的更多相关文章
- 【COGS 1873】 [国家集训队2011]happiness(吴确) 最小割
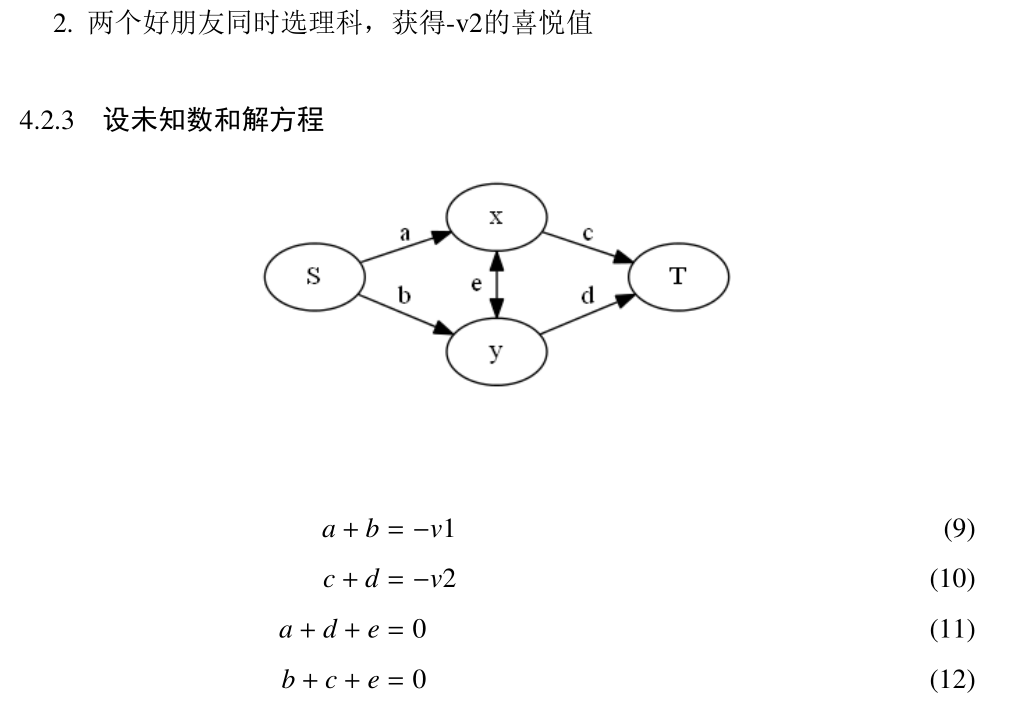
这是一种最小割模型,就是对称三角,中间双向边,我们必须满足其最小割就是满足题目条件的互斥关系的最小舍弃,在这道题里面我们S表示文T表示理,中间一排点是每个人,每个人向两边连其选文或者选理的价值,中间每 ...
- POJ 3469 Dual Core CPU (最小割建模)
题意 现在有n个任务,两个机器A和B,每个任务要么在A上完成,要么在B上完成,而且知道每个任务在A和B机器上完成所需要的费用.然后再给m行,每行 a,b,w三个数字.表示如果a任务和b任务不在同一个机 ...
- POJ 3084 Panic Room (最小割建模)
[题意]理解了半天--大意就是,有一些房间,初始时某些房间之间有一些门,并且这些门是打开的,也就是可以来回走动的,但是这些门是确切属于某个房间的,也就是说如果要锁门,则只有在那个房间里才能锁. 现在一 ...
- 【GCJ2008E】日程表 最小割
Google Code Jam 2008 E 日程表 [题目描述] 热情的选手Sphinny正在看新一年的日程表,并发现已经安排了很多编 程竞赛.她将这一年的每一天都用以下三种方式之一在日程表上打标记 ...
- [bzoj 1001][Beijing2006]狼抓兔子 (最小割+对偶图+最短路)
Description 现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的, 而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一 ...
- CodeForces1082G Petya and Graph 最小割
网络流裸题 \(s\)向点连边\((s, i, a[i])\) 给每个边建一个点 边\((u, v, w)\)抽象成\((u, E, inf)\)和\((v, E, inf)\)以及边\((E, t, ...
- bzoj 1412 最小割 网络流
比较明显的最小割建模, 因为我们需要把狼和羊分开. 那么我们连接source和每个羊,流量为inf,代表这条边不能成为最小割中的点,同理连接每个狼和汇,流量为inf,正确性同上,那么对于每个相邻的羊和 ...
- SP839 Optimal marks(最小割)
SP839 Optimal marks(最小割) 给你一个无向图G(V,E). 每个顶点都有一个int范围内的整数的标记. 不同的顶点可能有相同的标记.对于边(u,v),我们定义Cost(u,v)= ...
- 【bzoj1976】[BeiJing2010组队]能量魔方 Cube 网络流最小割
题目描述 一个n*n*n的立方体,每个位置为0或1.有些位置已经确定,还有一些需要待填入.问最后可以得到的 相邻且填入的数不同的点对 的数目最大. 输入 第一行包含一个数N,表示魔方的大小. 接下来 ...
随机推荐
- mongodb安装的两条命令
1. 安装 下载并安装,注意安装方式为custom,路径自定义(d:\chengxu\mongodb),安装成功后在mongodb文件夹下新建data文件夹(内新建db文件夹)和logs文件夹(内新建 ...
- Python-正确使用Unicode
正确处理文本,特别是正确处理Unicode.是个老生常谈的问题,有时甚至会难倒经验丰富的开发者.并不是因为这个问题很难,而是因为对软件中的文本,开发者没有正确理解一些关键概念及其表示方法.在Stack ...
- linux sudo命令详解
--sudo命令重启网卡 sudo service network restart http://bestchenwu.iteye.com/blog/1450292
- 使用struct与使用class初始化对象效率对比
using System; using System.Collections.Generic; using System.Diagnostics; using System.Linq; using S ...
- window.print
function contentPrint(contentArea) { var initBody = document.body.innerHTML; if ($("div"). ...
- python3 解析xml
转载:http://www.jb51.net/article/79494.htm 这篇文章主要为大家详细介绍了深入解读Python解析XML的几种方式,以ElementTree模块为例,演示具体使用方 ...
- iOS swift String 换行显示
在oc中换行的方式 NSString *str = @" aaaaa \ bbbbb \ cccc \ "; swift中这种方式不可用 ,swift中换行采用新的方双三引号 &q ...
- openssl基础
OpenSSL 是一个安全套接字层密码库,囊括主要的密码算法.常用的密钥和证书封装管理功能及SSL协议,并提供丰富的应用程序供测试或其它目的使用. OpenSSL is an open source ...
- Generating SSH Keys on windows
two ways here I provide: use openSSH command line on git bash(such as msysgit bash) ls -al ~/.ssh ss ...
- 【犀牛书笔记】JavaScript正则表达式的模式匹配
正则表达式,是一个描述字符模式的对象. JavaScript用RegExp类表示正则表达式 String和RegExp都定义了相关方法 原创文章,转载请注明:http://www.cnblogs.co ...
