Anniversary party（树上dp+HDU1520）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1520

题目：

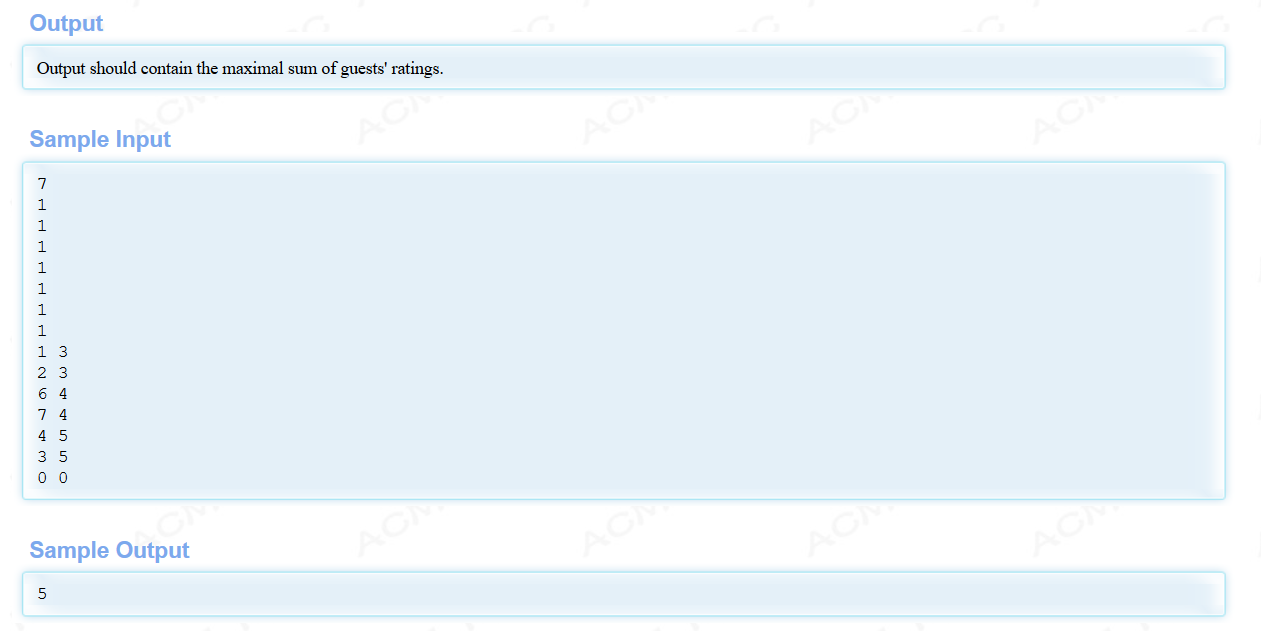
题意：一个学校要办校庆，校长决定邀请员工参加，但是下属和他的直系同时参加的话，下属将会无法开心的玩（每个人都有一个开心值），问怎样邀请才能使得总的开心值最大。（关系图为树形）

思路：树形dp，每个人都有邀请和不邀请两种状态。加入邀请了当前这个人，那么就不能邀请他的下属；如果不邀请当前这个人，那么既可以邀请他的下属，也可以不邀请他的下属，为了让总的开心值最大，取他的下属两种情况下子树开心值的最大值。我们用dp[i][j]来记录以这个点为根节点得子树的最大开心值，dp[i][0]表示不邀请当前节点，dp[i][1]表示邀请当前节点。由刚刚的分析我们得知：dp[i][1]+=dp[j][0],dp[i][0]+=max(dp[j][0],dp[j][1])，其中j为i的子节点，最后答案就是max(dp[s][1],dp[s][0])，其中s是根节点，由题意知本题根节点为1。树形dp一般都是用dfs来进行处理，而信息的传递有从子节点传向父亲节点和从父亲节点到子节点两种情况，而本题显然是选择第一种信息传递方式。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef unsigned long long ull;

 #define bug printf("*********\n");
 #define FIN freopen("in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const int mod = 1e9 + ;
 const int maxn = 6e3 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f3f;

 int n, s, u, v;
 int dp[maxn][], in[maxn];
 vector<int> G[maxn];

 void dfs(int u) {
     int v;
     for(int i = ; i < G[u].size(); i++) {
         v = G[u][i];
         dfs(v);
         dp[u][] += dp[v][];
         dp[u][] += max(dp[v][], dp[v][]);
     }
 }

 int main() {
     //FIN;
     while(~scanf("%d", &n)) {
         memset(in, , sizeof(in));
         for(int i = ; i <= n; i++) {
             scanf("%d", &dp[i][]);
             dp[i][] = ;
             G[i].clear();
         }
         while(~scanf("%d%d", &u, &v) && u && v) {
             G[v].push_back(u);
             in[u]++;
         }
         for(int i = ; i <= n; i++) {
             if(in[i] == ) {
                 s = i;
                 break;
             }
         }
         dfs(s);
         printf("%d\n", max(dp[s][], dp[s][]));
     }
     return ;
 }