Siki_Unity_3-13_编程内功修炼-算法

Unity 3-13 编程内功修炼 -- 算法

任务1&2：课程介绍

主要算法：
　　分治法
　　堆排序
　　二叉树
　　动态规划
　　贪心算法
　　图

任务3：分治算法 -- Divide and Conquer

分治算法：对于一个规模为n的问题，若该问题可以容易地解决（n较小），则直接解决
　　否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同
　　递归地解决这些子问题，然后将各子问题的解合并得到原问题的解。

使用分治法求解的一些经典问题：
　　二分搜索
　　大整数乘法
　　Strassen矩阵乘法
　　棋盘覆盖
　　合并排序
　　快速排序
　　线性时间选择
　　最接近点对问题
　　循环赛日程表
　　汉诺塔

任务4：最大子数组问题
&5：暴力求解最大子数组问题
&6&7：分治法求解最大子数组问题

最大子数组问题：

已知17天的股票价格， 问哪一天买入哪一天卖出收益最高

--> 问题转化：价格波动的哪一个子数组为最大子数组

任务5：暴力求解：

// Siki老师的方法
int[] priceArray = { , , , , , , , , , 
　　　　　　　　　　101, , , , , , ,  };
int[] priceFluctuationArray = new int[priceArray.Length - ];//价格波动的数组
for (int i = ; i < priceArray.Length; i++) {
    priceFluctuationArray[i - ] = priceArray[i] - priceArray[i - ];
}
int total = priceFluctuationArray[];//默认数组的第一个元素 是最大子数组
int startIndex = ;
int endIndex = ;
for (int i = ; i < priceFluctuationArray.Length; i++) {
    //取得以i为子数组起点的 所有子数组
    for (int j = i; j < priceFluctuationArray.Length; j++) {
        //由i j 就确定了一个子数组
        int totalTemp = ;//临时 最大子数组的和
        for (int index = i; index < j + ; index++) {
            totalTemp += priceFluctuationArray[index];
        }
        if (totalTemp > total) {
            total = totalTemp;
            startIndex = i;
            endIndex = j;
        }
    }
}
Console.WriteLine("startindex : " + startIndex);
Console.WriteLine("endIndex : " + endIndex);
Console.WriteLine("购买日期是第"+startIndex+"天, 出售是第"+(endIndex+)+"天" 
　　　　　　　　　　+ "；盈利：" + total);
Console.ReadKey();

我自己的改良方法：O(n^2)

// 已知股票的价格数组
int[] priceArray = { , , , , , , , , ,
                    , , , , , , ,  };
// 求价格波动的数组
int[] priceFluctuationArray = new int[priceArray.Length-];
for (int i = ; i < priceArray.Length; i++) {
    priceFluctuationArray[i - ] = priceArray[i] - priceArray[i - ];
}
// 计算每个子数组的值
// 从i到j的子数组
int maxInterest = priceFluctuationArray[];
int startDate = ;
int endDate = ;
for (int i = ; i < priceFluctuationArray.Length; i++)  {
    int interest = ;
    // 子数组头
    for (int j = i; j < priceFluctuationArray.Length; j++) {
        // 子数组尾
        interest += priceFluctuationArray[j];
        if(interest > maxInterest) {
            startDate = i;
            endDate = j;
            maxInterest = interest;
        }
    }
}
Console.WriteLine("From " + startDate + " to " + (endDate+)
                + "; interest: " + maxInterest);
Console.ReadKey();

任务6：分治法求解

策略：
　　1. 设low为数组开始的index，high为数组结束的index
　　　　[low, high]
　　2. 取mid的index
　　　　[low, mid]  [mid+1, high]
　　　　设i, j分别为最大子数组的开始索引和结束索引
　　　　三种情况：
　　　　　　a) i, j同时位于低区间
　　　　　　b) i, j同时位于高区间
　　　　　　c) i位于低区间，j位于高区间
　　　　分别求出这三种情况的最大子数组；比较这三个最大子数组，求出最大子数组
　　　　a和b情况均为将大数组变为小数组，可以使用递归来解决（分解为最小）
　　　　c情况很容易做到：分别取得i~mid的最大值，j~mid的最大值即可：O(n)
　　3. 重复步骤2（递归）

代码实现：

1. Main
　　求完priceFluctuationArray后
　　GetMaxSubArray(0, priceFluctuationArray.Length-1, priceFluctuationArray);
　　来得到最大子数组

2. 定义GetMaxSubArray();
　　返回值需要最大子数组的startIndex、endIndex和price的总和
　　因此设返回值为一个struct
　　Struct SubArray {
　　　　int startIndex; int endIndex; int total;
　　}

3. 定义GetMaxSubArray()为：
　　static SubArray GetMaxSubArray(int low, int high, int[] array);

4. 得到mid的值
　　int mid = (low + high) / 2;

5. 三种情况分别讨论

a) i, j 在低区间
　　GetMaxSubArray(low, mid, array);
　　// 需要保存返回值，因为最后要比较三种情况，得出最大子数组
　　SubArray subArray1 = GetMaxSubArray(...);

b) i, j 在高区间
　　SubArray subArray2 = GetMaxSubArray(mid+1, high, array);

c) i 在低区间，j 在高区间
　　// 不需调用，可以直接解决 -- 一个for循环

// i 在低区间 [low, mid] 找到最大子数组 [i, mid]
int maxLowTotal = array[mid];
int lowTotal = array[mid];
int startIndex = mid;
for (int i = mid-1; i >= low; i--) {
　　lowTotal += array[i];
　　if (lowTotal > maxLowTotal) {
　　　　maxLowTotal = lowTotal;
　　startIndex = i;
}}

// j 在高区间 [mid+1, high] 找到最大子数组 [mid+1, j]
for (int j = mid+1; j<= high; j++) {
　　highTotal += array[j];
　　if (highTotal > maxHighTotal) {
　　　　maxHighTotal = highTotal;
　　endIndex = j;
}}

// 得到该情况下的最大子数组
SubArray subArray3;
subArray.startIndex = startIndex;
subArray.endIndex = endIndex;
subArray.total = maxLowTotal + maxHighTotal;

6. 比较这三种情况下哪一个最大子数组会成为最终的最大子数组

if (subArray1.total >= subArray2.total && subArray1.total >= subArray3.total) {
　　return subArray1;
} else if (subArray2.total >= subArray1.total && subArray2.total >= subArray3.total) {
　　return subArray2;
} else {
return subArray3;
}

7. 那么，递归什么时候是个头呢？
　　当小数组只有一个元素的时候，即low=high的时候
　　此时，这个小数组的最大子数组就是本身
　　if(low == high) {
　　　　SubArray subArray = new SubArray();
　　　　subArray.startIndex = low;
　　　　subArray.endIndex = high;
　　　　subArray.total = array[low];
　　　　return subArray;
　　}

namespace 最大子数组问题___分治法 {
    class Program {

        //最大子数组的结构体
        struct SubArray {
            public int startIndex;
            public int endIndex;
            public int total;
        }
        static void Main(string[] args) {
            int[] priceArray = { , , , , , , , , 
　　　　　　　　　　　　　　　　　　81, , , , , , , ,  };
            int[] priceFluctuationf = new int[priceArray.Length - ];
            for (int i = ; i < priceArray.Length; i++) {
                priceFluctuationf[i - ] = priceArray[i] - priceArray[i-];
            }

            SubArray subArray = GetMaxSubArray(, priceFluctuationf.Length-,
                                        priceFluctuationf);
            Console.WriteLine(subArray.startIndex);
            Console.WriteLine(subArray.endIndex);
            Console.WriteLine("我们在第" + subArray.startIndex + "天买入，在第"
                                    + (subArray.endIndex + ) + "天卖出");
            Console.ReadKey();
        }

        // 这个方法是用来取得array 这个数组 从low到high之间的最大子数组
        static SubArray GetMaxSubArray(int low, int high, int[] array) {
            if (low == high) {
                // 分治到最小部分
                SubArray subArray;
                subArray.startIndex = low;
                subArray.endIndex = high;
                subArray.total = array[low];
                return subArray;
            } else {
                // 三种情况
                // a) i, j同时位于低区间
                //  b) i, j同时位于高区间
                // c) i位于低区间，j位于高区间

                int mid = (low + high) / ;
                // a)
                SubArray subArray1 = GetMaxSubArray(low, mid, array);
                // b
                SubArray subArray2 = GetMaxSubArray(mid + , high, array);
                // c
                // i 在低区间 [low, mid] 找到最大子数组 [i, mid]
                int maxLowTotal = array[mid];
                int lowTotal = array[mid];
                int startIndex = mid;
                for (int i = mid - ; i >= low; i--) {
                    lowTotal += array[i];
                    if (lowTotal > maxLowTotal) {
                        maxLowTotal = lowTotal;
                        startIndex = i;
                    }
                }
                // j 在高区间 [mid+1, high] 找到最大子数组 [mid+1, j]
                int maxHighTotal = array[mid + ];
                int highTotal = array[mid + ];
                int endIndex = mid + ;
                for (int j = mid + ; j <= high; j++) {
                    highTotal += array[j];
                    if (highTotal > maxHighTotal) {
                        maxHighTotal = highTotal;
                        endIndex = j;
                    }
                }
                SubArray subArray3;
                subArray3.startIndex = startIndex;
                subArray3.endIndex = endIndex;
                subArray3.total = maxLowTotal + maxHighTotal;
                //  比较这三种情况下哪一个最大子数组会成为最终的最大子数组
                if (subArray1.total >= subArray2.total
                        && subArray1.total >= subArray3.total) {
                    return subArray1;
                } else if (subArray2.total >= subArray1.total
                        && subArray2.total >= subArray3.total) {
                    return subArray2;
                } else {
                    return subArray3;
                }
            }
        }
    }
}           

任务8：树（数据结构）

树 (Tree)是n(n>=0)个结点的有限集。
n=0时称为空树
在任意一棵非空树中，1. 有且仅有一个特定的结点称为根结点 (root)
　　2. 当n>1时，其余结点可分为m(m>0)个互不相交的有限集，其中每个集合本身又是一棵树
　　　　并称为根的子树 (SubTree)

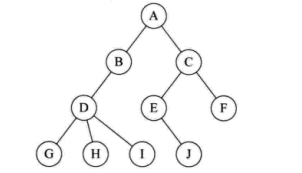
一些概念：

结点的度：拥有子树的个数
树的层次：根结点为第一层，根结点的子结点为第二层，以此类推
树的深度：最大的层次
兄弟关系：有同一个父亲结点的两个子结点之间的关系为兄弟关系（如G和H）
　　堂兄弟关系：层次相同（没有共同父亲的即为堂兄弟，如I和J）
一个结点只能有一个父结点，子树之间是不相交的

任务9：树的存储结构

存储结构：顺序存储和链式存储
　　如果使用顺序存储(数组)，结点之间的关系就很难表示出来
　　因此使用链式存储：
　　　　1. 双亲表示法 -- 
　　　　　 优点：可以很方便地访问父亲结点
　　　　　 缺点：不容易访问兄弟结点和子结点
　　　　2. 孩子表示法 -- 
　　　　　 优点：通过父亲能很方便地访问所有子结点
　　　　　 缺点：不容易访问父亲结点和兄弟结点；
　　　　　　　　 浪费空间：每个结点的孩子数量不同，有很多指向孩子地址的空间为null

　　　　3.孩子兄弟表示法 -- 
　　　　　 保存了第一个孩子和右边的兄弟

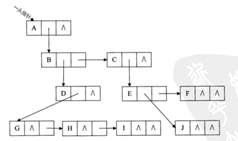
　优点：方便地访问所有的子结点（通过firstchild访问rightsib即可）
　　　　方便地访问它的兄弟
　缺点：不容易访问父结点

4. 还有其他表示法

任务10&11：二叉树的定义和性质（满二叉树、完全二叉树）

二叉树 (Binary Tree)：每个结点最多有两个子结点（子结点有左右的顺序）

左右子树：每个结点可能有一个左子树和/或一个右子树

特殊二叉树：
　　斜树：（左斜树、右斜树）：所有结点只有左 (右)子树的二叉树
　　满二叉树：树的任意一个结点都有两个子结点（叶子结点没有子结点）
　　完全二叉树：对一棵具有n个结点的二叉树按层序编号，如果编号为i (1<=i<=n)的结点与同
　　　　样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则该树为完全二叉树
　　　　（树的任意一个结点都有两个子结点（最后一层叶子结点可以从右开始连续缺失））
　　满二叉树一定是完全二叉树，反之就不对了

二叉树的性质：
　　二叉树的第i层上最多有2^(i-1)个结点
　　深度为k的二叉树至多有2^k-1个结点
　　　　　　2⁰+2¹+2²+2³+2⁴+...+2^k-1
　　　　　=  2⁰+2¹+2²+2³+2⁴+...+2^k-1 + 1 - 1
　　　　　=  1 + 2⁰+2¹+2²+2³+2⁴+...+2^k-1 - 1
　　　　　=  2⁰ + 2⁰+2¹+2²+2³+2⁴+...+2^k-1 - 1
　　　　　=  2^k - 1
　　n个结点的完全二叉树，对结点从1开始编号（按满二叉树的方式），对任意结点i有：
　　　　a) 它的父结点是 i/2
　　　　b) 它的左孩子是 2i, 右孩子是2i+1
　　　　c) 如果2i>n 说明无子结点；如果2i+1>n说明无右孩子

任务12：二叉树的存储结构

对于一般树来说，使用链式存储比较方便。
但是对于二叉树来说，兄弟、父亲、孩子可以很方便的通过编号得到，所以使用顺序存储

顺序存储：将所有二叉树都当作完全二叉树来存储
　　依次按结点编号(从1开始)放入数组（编号=index+1）
　　不存在的结点=null即可 -- 非完全二叉树会有空间浪费

链式存储：结点结构：

无法方便地访问父结点；一个结点需要三倍内存空间；
头结点head指向根结点；每个结点的两个指针指向存在的子结点

任务13：二叉树的四种遍历方法

二叉树的遍历是指：从根结点出发，按照某种次序依次访问二叉树中的所有结点，使每个结点仅被访问一次

前序遍历：先输出当前结点的数据，再依次遍历输出左结点和右结点
　　ABDGHCEIF

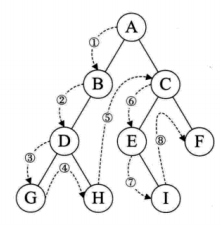
中序遍历：先遍历输出左结点，再输出当前结点的数据，再遍历输出右结点
　　GDHBAEICF

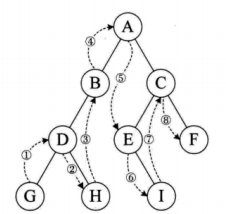
后序遍历：先遍历输出左结点，再遍历输出右结点，最后输出当前结点的数据
　　GHDBIEFCA

层序遍历：从树的第一层开始，从上到下逐层遍历；同一层中，从左到右对结点逐个访问输出
　　ABCDEFGHI

任务14&15&16：代码实现二叉树的顺序存储和遍历

使用数组实现二叉树

class BiTree<T> {
    private T[] data;
    private int count = ;

    public BiTree(int capacity) {
        data = new T[capacity];
    }

    public bool Add(T item) {
        if (count >= data.Length) {
            // 二叉树满了
            return false;
        }
        data[count] = item;
        count++;
        return true;
    }
    ...
}

二叉树的遍历：

前序遍历：void FirstTraversal(int index) {
　　　　// index为想要遍历的索引
　　　　// 先输出结点数据
　　　　Console.Write(data[index]);
　　　　// 得到要遍历的结点编号
　　　　int number = index + 1;
　　　　// 遍历左子结点
　　　　FirstTraversal(number * 2 - 1);  // index = number - 1
　　　　// 遍历右子结点
　　　　FirstTraversal(number * 2 + 1 - 1);
　　　　}

但是，每一种递归都需要一个终止条件，当结点没有子结点的时候，即可返回
　　if(index >= data.Length)  return;

而且，当二叉树不是完全二叉树时，需要判断结点是否为空
　　if(data[index] == null)  return;

如何开始遍历呢？遍历编号为1的结点即可；
　　外界调用封装好的方法 public void FirstTraversal();
　　public void FirstTraversal() {
　　　　FirstTraversal(0);
　　}
　　并设FirstTraversal(int index) 为 private

// siki老师的方法
public void FirstTraversal() {
    FirstTraversal();
}
private void FirstTraversal(int index) {
    if (index >= count) return;
    //得到要遍历的这个结点的编号
    int number = index + ;
    if (data[index].Equals(-)) return;
    Console.Write(data[index] + " ");
    //得到左子结点的编号
    int leftNumber = number * ;
    int rightNumber = number *  + ;
    FirstTraversal(leftNumber - );
    FirstTraversal(rightNumber - );
}

// 我的方法
public void FirstTraversal() {
    FirstTraversal();
}

private void FirstTraversal(int index) {
    // index为想要遍历的索引
    // 先输出结点数据
    if(data[index ] == null) {
        return;
    }
    Console.Write(data[index]);
    // 得到要遍历的结点编号
    int number = index + ;
    if (number*<=count) {
        // 遍历左子结点
        FirstTraversal(number *  - );
    }
    if(number *  +  <= count) {
        // 遍历右子结点
        FirstTraversal(number *  +  - );
    }
}

中序遍历：

后序遍历：

层序遍历：

任务17：二叉排序树/ 二叉查找树

二叉排序树：对于任意结点，若左子树不为空，则左子树上所有结点的值均小于根结点的值
　　若右子树不为空，则右子树上所有结点的值均大于根结点的值

优点：排序方便（直接通过中序遍历就能得到有序结果），
　　　查找方便（从根结点开始，判断往左/ 右子树继续查找即可）
　　　插入方便（与查找相似）

二叉排序树的删除操作：
　　1. 删除叶子结点：直接删除
　　2. 删除的结点只有一个子结点(左图)：用子结点替换掉被删除的结点
　　　 删除的结点只有一个子树(右图)：用子树的根结点替换掉被删除的结点

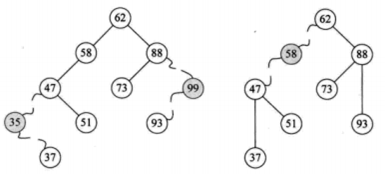
37替代35，93替代99　　　　　　47替代58，直接建立47~62的连接

3. 删除的结点有两个子结点/子树：
　　需要选出所有子结点中间大小的结点
　　a) 找到左子树中的最右子结点（for遍历所有的右结点）（左子树中的最大值）
　　b) 找到右子树中的最左子结点（for遍历所有的左结点）（右子树中的最小值）

链式结构：由于二叉树的结点的位置由自身值的大小有关系，因此需要使用链式结构存储

任务18&19&20&21：二叉排序树的代码实现

添加操作

。。。

排序和查找

。。。

查找方法的优化

。。。

删除操作

。。。

任务22：堆和堆排序

堆：完全二叉树
　　大顶堆：每个结点的值都大于或等于其孩子结点的值
　　小顶堆：每个结点的值都小于或等于其孩子结点的值

堆排序：利用堆来进行排序
　　将待排序的序列构造成一个大顶堆，此时整个序列的最大值就是根结点。
　　将它和堆的最后一个元素交换，此时末尾元素就是最大值
　　将剩余的n-1个序列重新构造成一个堆，这样就会得到n各元素中的次小值
　　反复执行就能得到一个有序序列

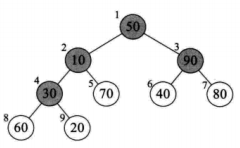
思路：
　　使用顺序结构存储完全二叉树
　　构造大顶堆：
　　　　叶子结点本身是一个大顶堆，无序遍历
　　　　将[30, 60, 20]构造成一个大顶堆 --> 取最大值60，与根结点30交换即可
　　　　将[10, 60, 70]构造成一个大顶堆 --> 取最大值70，与根结点10交换即可
　　　　　　但是交换之后，编号为4的结点发生了变化，需要遍历以下整棵子树构造大顶堆

任务23：大顶堆的代码实现

。。。

任务24：堆排序的代码实现

。。。

。。。

任务25：动态规划算法  (Dynamic Programming)

动态规划算法：基于一个递归公司及一个或多个初始状态。
　　当前子问题的解由上一次子问题的解推出。
　　动态规划和分治法相似，都是通过组合子问题的解来求解原问题。
　　　　分治法：问题划分成互不相交的子问题，递归求解子问题，再将子问题的解组合
　　　　动态规划：子问题重叠（不同子问题具有公共的子子问题）。
　　　　　　此时分治法会反复求解那些公共子问题 (没必要)
　　　　　　而动态规划算法对每个子子问题求解一次，并将结果保存，无需重新计算

动态规划的方法进行求解：
　　动态规划算法安排求解的顺序，对每个子问题只求解一次，并将结果保存下来。
　　如果随后再次需要此子问题的解，只需查找保存的结果，不必重新计算。
　　因此动态规划的方法是付出额外的内存空间，来节省计算时间。

动态规划的两种实现方法：
　　方法一：带备忘的自顶向下法
　　　　按照自然的递归形式编写过程，但过程中会保存每个子问题的解（通常保存在一个数组中）。
　　　　当需要计算一个子问题的解时，过程首先检查是否已经保存过此解。
　　　　如果是，则直接返回保存的值，从而节省了计算时间；
　　　　如果没有保存过此解，按照正常方式计算这个子问题。
　　方法二：自底向上法
　　　　首先恰当的定义子问题的规模，使得任何问题的求解都只依赖于更小的子问题的解。
　　　　因而我们将子问题按照规模排序，按从小到大的顺序求解。
　　　　当求解某个问题的时候，它所依赖的更小的子问题都已经求解完毕，结果已经保存。

两个实例讲解动态规划算法：
　　钢条切割问题（见任务26）
　　背包问题（见任务31）

任务26&27：钢条切割问题分析（动态规划）

已知出售一段长度为i英寸的钢条的价格为pi (i=1,2,3...)。
给一段长度为n的钢条，问怎么切割收益r_n最大

比如：
　　n=1： 长度为1，价格为1
　　n=2： 长度为2，价格为5；
　　　　　长度为1+1，价格为1+1=2；
　　n=3： 长度为3，价格为8；
　　　　　长度为1+2，价格为1+5=6；
　　　　　长度为1+1+1，价格为1+1+1=3；
　　n=4： 长度为4，价格为9；
　　　　　长度为1+3，价格为1+8=9；
　　　　　长度为1+1+2，价格为1+1+5=7；
　　　　　长度为1+1+1+1，价格为1+1+1+1=4；
　　　　　长度为1+2+1，价格为1+5+1=7；
　　　　　长度为2+2，价格为5+5=10；
　　　　　长度为2+1+1，价格为5+1+1=7；
　　　　　长度为3+1，价格为8+1=9；

假设最优解把n段切割成了k段：n = i₁ + i₂ + i₃ + ... + i_k (1<=k<=n)
　　最大收益r_n = p_i1 + p_i2 + p_i3 + ... + p_ik

求解方案：

第一种方案：（递归求解，递归太多，过于复杂）

1. 不切割：收益为p_n
2. 切割成两半：分解为两个子问题
r_n = max(p_n, (r₁ + r_n-1), (r₂ + r_n-2), ... , (r_n-1 + r₁))

第二种方案：

从钢条的左边切下长度为i (i=n即不切割(i!=0))的一段，
只对右边剩下长度为n-i的一段继续切割
rn = max((p₁ + r_n-1), (p₂ + r_n-2), ... , (p_n-1 + r₁), (p_n + 0))
与第一种方案的区别：
每次递归调用的时候只需递归一种情况而不是两种情况

代码实现：自顶向下递归实现（求r_n需要求r_n-1，求r_n-1需要求r_n-2，最后需要求r₁）

任务28&29&30：钢条切割问题的三种代码实现

。。。

。。。

。。。

任务31：0-1背包问题简介
&33：背包问题的动态规划分析

有容量m kg的背包，另外有i种 (1~i)物品 (每种只有一个)，总量分别为w[1] w[2] ... w[i] (kg)
　　价值分别为p[1] p[2] ... p[i] (元)
　　问将哪些物品放入背包可以使得背包的总价值最大？最大价值是多少？

穷举法：把所有情况列出来，比较得到总价值最大的情况（O(2ⁿ)）

动态规划：i个物品放入容量为m(kg)的背包的最大价值 (记为c[i, m])
　　对于每种物品只有两种选择：装入 或 不装入 -- 01背包问题
　　每种物品不能装入多次

对于c[i. m]有几种情况：
　　c[i, 0] = c[0, m] = 0;
　　c[i, m] = c[i-1, m] (w[i]>m) 
　　当w[i]<=m时，两种情况：
　　　　不放入i，c[i, m] = c[i-1, m]
　　　　放入i，c[i, m] = c[i-1, m-w[i]] + p(i)
　　　　--> c[i, m] = max(放入i, 不放入i)
将c[i, m]的问题分解为小问题，直到c[0, m]或c[i, 0]返回 -- 递归 -- 自顶向下
大问题依赖着小问题，从小问题向上解决到大问题也可以完成 -- 自底向上

任务32：使用穷举法实现背包问题

。。。

任务34&35&36：三种方式实现背包问题（代码）
　　（不带备忘的自顶向下法/ 带备忘的自顶向下法/ 自底向上法）

。。。

。。。

。。。

任务37：贪心算法

对于许多最优化问题 (钢条切割问题--最大收益/ 背包问题--最大价值)，使用动态规划算法有些没必要
　　可以使用更加简单高效的算法 -- 贪心算法
贪心算法在每一步做出当时看起来最佳的选择，即从每一次局部最优的选择，得到最后全局最优解
　　对于某些问题并不能保证得到最优解，但对很多问题确实可以得到最优解。
　　但即使某些时候不能得到最优解（而是次优解），我们也可能会选择贪心算法求解 -- 高效

任务38：活动选择问题（贪心算法）

有n个需要在同一天使用同一个教室的活动a1, a2, ..., an，教师同一时刻只能由一个活动使用。
　　每个活动ai都有一个开始时间si和结束事件fi；一旦被选择后，活动ai就占据时间区间 [si, fi)
　　如果 [si, fi) 和 [sj, fj) 互不重叠，ai和aj两个活动就可以被安排在这一天。
　　活动选择问题：安排这些活动，使尽量多的活动能不冲突地在这一天举行 (最大兼容活动子集)
　　注：是尽量多的活动，而不是尽可能长的时间
　　最大兼容子集可能不是唯一的。

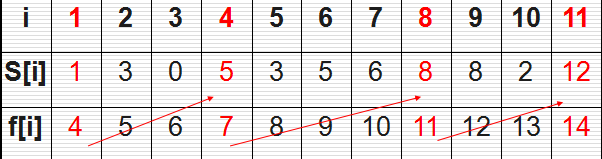
　　如：{a1, a4, a8, a11} 和 {a2, a4, a9, a11} 都是最大兼容子集

任务39&40&41：动态规划思路解决活动选择问题

。。。

。。。

。。。

任务42&43&44：贪心算法解决活动选择问题

什么是局部最优选择：
　　对于任何非空集合S，若a_m是S中结束时间最早的活动，则a_m一定在S的某个最大兼容子集中
　　证明 -- 反证法：
　　　　反证：a_m不在任意一个S的最大兼容子集中
　　　　证明1号活动不在最大兼容子集中
　　　　　　如果1号活动在最大兼容子集中，则最大兼容子集为1号活动 + [4, 24)中的最大兼容子集
　　　　　　如果1号活动不在最大兼容子集中，则后面肯定有一个活动是在最大兼容子集中的
　　　　　　　　假如是3号，则最大兼容子集为3号活动 + [6, 24)中的最大兼容子集
　　　　　　　　而[4, 24)肯定比[6, 24)的时间长，因此a₃开始的兼容子集肯定不会比a₁开始的大
　　　　　　那么如果3号开始的兼容子集最大，那么1号开始的也肯定是最大兼容子集 (数量相等)
　　　　　　因此1号活动肯定在最大兼容子集中
　　　　因此a1一定在S的某个最大兼容子集中。

无法一步到位直接找到最大兼容子集的话，寻找局部最优选择（找到头活动--结束时间最早）

1. 将所有活动按照结束时间早晚进行排序
2. 判断开始时间是否满足条件 + 比较结束时间是否最早 (无需判断，因为已经有序)：遍历即可

　　在(0-24)这段时间中，1号活动一定在最大兼容子集中（结束时间最早）
　　剩下(4~24)这段时间，寻找4点以后开始，结束时间最早的活动 -- 子问题

。。。

。。。

。。。

任务45：钱币找零问题（贪心算法）

假设1元、2元、5元、10元、20元、50元和100元纸币分别有c0, c1, ... c6张来支付K元，至少要几张

贪心算法：每一步尽可能用面值大的纸币

static void Main(string[] args) {
    int[] count = { , , , , , ,  };
    int[] amount = { , , , , , ,  };
    int[] result = Change(, count, amount);
    foreach (int i in result) {
        Console.Write(i + " ");
    }
    Console.ReadKey();
}

public static int[] Change(int k, int[] count, int[] amount) {
    int[] result = new int[count.Length + ]; // 最后一位表示未支付金额
    // 当k的金额比所有纸币的总额都大，无法达到要求
    // 当小面额的纸币不够补足k的零头，无法达到要求，比如本例中k=4时
    for (int i = count.Length - ; i >= ; i--)  {
        if(k<=) { break; }
        // 情况1：k比该面额大
        // 情况2：k比该面额小
        if (count[i] >= k / amount[i]) {
            result[i] = k / amount[i];
            k %= amount[i];
        } else {
            // 情况3：该面额数量太少，没有足够该面额纸币
            result[i] = count[i];
            k -= (count[i] * amount[i]);
        }
    }
    result[result.Length - ] = k; // 最后一位存储未支付金额
    return result;
}

任务46：图

图的主要应用是在地图上，如导航寻路等；
　　如地图上有一个物品，需要自动寻路捡起该物品 -- 求最短路径

图 Graph：由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为 G<V,E> (Vertex, Edge)
　　注：图的顶点不能是空的，但是边可以为空
　　顶点之间的关系：多对多

图的有关定义：
　　无向边：顶点之间的边没有方向，用无序偶对(v_iv_j)表示
　　无向图 (Undirected graph)：图中任意两个顶点之间的边都是无向边
　　有向边/ 弧 (Arc)：用有序偶对<v_i, v_j>表示从v_i到v_i的有向边，v_i为弧尾(Tail)，vj为弧头(Head)
　　简单图：不存在顶点到自身的边，且同一条边不重复出现
　　连通图 (Connected graph)：

图的存储：
　　邻接矩阵 Adjacency Matrix（两个数组，一维数组存储顶点信息，二维数组存储边或弧的信息）
　　邻接表 Adjacency List（数组与链表相结合，一维数组存储顶点和指向第一个邻接点的指针，
　　　　便于查找该顶点的边信息，每个顶点vi的所有邻接点构成一个线性表（单链表））
　　十字链表 Orthogonal List：把邻接表和逆邻接表结合起来
　　　　（邻接表关心了出度问题，逆邻接表关心了入度问题）
　　邻接多重表......
　　边集数组......

图的遍历：
　　深度优先 Depth First Search (DFS)：类似于树的前序遍历
　　　　从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发，深度优先遍历图，
　　　　直到图中所有和v有路径相通的顶点都被访问到
　　　　对于非连通图：若图中还有顶点未被访问，则另选图中一个未曾访问的顶点开始DFS
　　广度优先 Breadth First Search (BFS)：类似于树的层序遍历

　　最小生成树 Minimum Cost Spanning Tree：构造连通网的最小代价生成树
　　　　Prim算法：
　　　　Kruskal算法：

最短路径：
　　Dijkstra算法：按路径长度递增的次序 O(n²)
　　　　一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上求得
　　　　更远顶点的最短路径
　　　　注：要求图中不存在负权边
　　Floyd算法：

拓扑排序：

关键路径：