洛谷 P2680 运输计划-二分+树上差分(边权覆盖)

P2680 运输计划

题目背景

公元 20442044 年,人类进入了宇宙纪元。

题目描述

公元20442044 年，人类进入了宇宙纪元。

L 国有 nn 个星球，还有 n-1n−1 条双向航道，每条航道建立在两个星球之间，这 n-1n−1 条航道连通了 LL 国的所有星球。

小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 u_iui​ 号星球沿最快的宇航路径飞行到 v_ivi​ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 jj，任意飞船驶过它所花费的时间为 t_jtj​，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， LL 国国王同意小 PP 的物流公司参与 LL 国的航道建设，即允许小PP 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 mm 个运输计划。在虫洞建设完成后，这 mm 个运输计划会同时开始，所有飞船一起出发。当这 mm 个运输计划都完成时，小 PP 的物流公司的阶段性工作就完成了。

如果小 PP 可以自由选择将哪一条航道改造成虫洞， 试求出小 PP 的物流公司完成阶段性工作所需要的最短时间是多少？

输入输出格式

输入格式：

第一行包括两个正整数 n, mn,m，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 11 到 nn 编号。

接下来 n-1n−1 行描述航道的建设情况，其中第 ii 行包含三个整数 a_i, b_iai​,bi​ 和 t_iti​，表示第 ii 条双向航道修建在 a_iai​ 与 b_ibi​ 两个星球之间，任意飞船驶过它所花费的时间为 t_iti​。数据保证 1 \leq a_i,b_i \leq n1≤ai​,bi​≤n 且 0 \leq t_i \leq 10000≤ti​≤1000。

接下来 mm 行描述运输计划的情况，其中第 jj 行包含两个正整数 u_juj​ 和 v_jvj​，表示第 jj 个运输计划是从 u_juj​ 号星球飞往 v_jvj​号星球。数据保证 1 \leq u_i,v_i \leq n1≤ui​,vi​≤n

输出格式：

一个整数，表示小 PP 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1： 复制

6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5

输出样例#1： 复制

11

说明

所有测试数据的范围和特点如下表所示

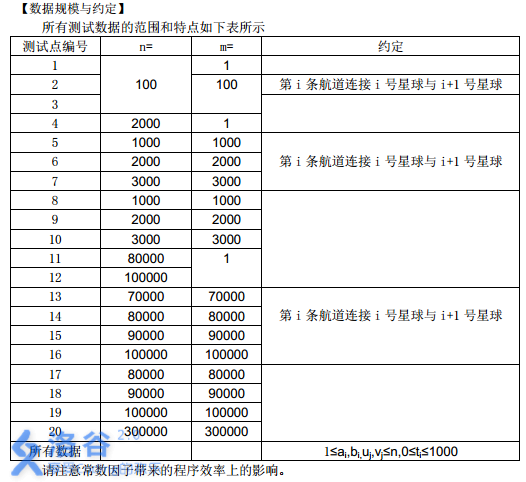
请注意常数因子带来的程序效率上的影响。

这道题有点东西。本来是想练手树上差分的，发现很多题解都是用二分+树链剖分写的，看了一下，树链剖分、线段树、树状数组(求线段标记次数)、LCA(有的是用tarjan求的路径的长度)。

一开始我看到这道题的时候，看到所有的计划都一起跑，就有点傻了，一起跑可怎么找，感觉直接暴力找回超时，后来算了一下，好像可以过。

我的思路就是：一开始的时候，先把所有的路径的长度出来，然后通过dfs把lca的相关东西处理出来，每一条线段的长度先保存一下，然后二分，最长的路径长度为右端点r，二分，每二分一次就遍历一下所有的路径，大于mid长度的，就树上差分保存一下，然后dfs一下就把所有的线段的标记次数找出来了，然后找一下是不是有某条线段被标记的次数为加入的路径的数量，如果有，就说明删掉这条边是可能成立的，最长的路径-这条线段与mid比较一下就可以了，有一点就是标记的次数相同的找最长的那条线段，一开始智障，找到了就跳出去了，wa了。。。

还有一点就是存边的时候数组开二倍，还有一点就是每一条线段的长度保存的时候，不能直接在输入的时候保存，这样会wa，因为用大的数当边的编号是对的，假设1和5相连，5和3相连，一开始1和5相连长度为3，输入的时候，我存的是vv[5]=3;但是等到我存5和3长度为5的时候，vv[5]=5,就不对了。soga，嘎嘎。

测评姬有点情绪不稳，相同的代码我第一次交有一个样例点tle，再交一次一模一样的，过了。。。试了好几次，网卡的时候就容易tle。。。

代码:

 //洛谷 P2680 运输计划 二分+树上差分(边覆盖)
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #include<cstdlib>
 using namespace std;
 typedef long long ll;
 const int maxn=3e5+;

 struct node{
     int to,val,next;
 }edge[maxn<<];

 int p1[maxn],p2[maxn],vv[maxn],maxx=,ret,num,n,m,cnt,ans;
 int head[maxn<<],sum[maxn],dep[maxn],fa[maxn][],dis[maxn],len[maxn];

 void add(int x,int y,int v){edge[++cnt].to=y,edge[cnt].val=v,edge[cnt].next=head[x],head[x]=cnt;}

 void dfs(int u,int fath)
 {
     dep[u]=dep[fath]+,fa[u][]=fath;
     for(int i=;fa[u][i];++i) fa[u][i+]=fa[fa[u][i]][i];
     for(int i=head[u];i;i=edge[i].next){
         int v=edge[i].to,w=edge[i].val;
         if(v!=fath) dis[v]=dis[u]+w,vv[v]=w,dfs(v,u);//vv的dfs一开始写挫了，直接写到输入那里了
     }
 }

 int LCA(int u,int v)
 {
     if(dep[u]>dep[v]) swap(u,v);
     for(int i=;i>=;i--) if(dep[u]<=dep[v]-(<<i)) v=fa[v][i];
     if(u==v) return u;
     for(int i=;i>=;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
     return fa[u][];
 }

 void Dfs(int u,int fath)//标记之后的Dfs
 {
     for(int i=head[u];i;i=edge[i].next){
         int v=edge[i].to;
         if(v==fath) continue;
         Dfs(v,u);
         sum[u]+=sum[v];
     }
     if(num==sum[u]){//如果标记的次数正好为加的边的数量，说明这一段在所有边上都有
         ret=max(ret,vv[u]);//标记次数相同的找长度最大的
     }
 }

 bool pig(int h)//判断
 {
     num=;ret=; memset(sum,,sizeof(sum));
     for(int i=;i<=m;i++){
         if(len[i]>h){
             num++;int lca=LCA(p1[i],p2[i]);
             sum[p1[i]]++;sum[p2[i]]++;sum[lca]-=;
         }
     }
     if(!num) return ;
     Dfs(,);return maxx-ret<=h;
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<n;i++){
         int u,v,w;
         scanf("%d%d%d",&u,&v,&w);
         add(u,v,w);add(v,u,w);//vv[max(u,v)]=w;
     }
     dfs(,);
     for(int i=;i<=m;i++){
         int x,y;
         scanf("%d%d",&x,&y);
         p1[i]=min(x,y);p2[i]=max(x,y);
         int lca=LCA(x,y);
         len[i]=dis[x]+dis[y]-*dis[lca];
         maxx=max(maxx,len[i]);
     }
     int l=,r=maxx;
     while(l<=r){
         int mid=(l+r)>>;//cout<<"mid= "<<mid<<endl;
         if(pig(mid))
             r=mid-;
         else
             l=mid+;
     }
     cout<<l<<endl;

 }
 /*
 6 3
 1 2 3
 1 6 4
 1 3 7
 3 4 6
 3 5 5
 3 6
 2 5
 4 5

 11

 */

不开心，最近状态不好，铁了一年了。唉，菜是原罪。