Topcoder Srm 673 Div2 1000 BearPermutations2

## $>Topcoder \space Srm \space 673 \space Div2 \space 1000 \space BearPermutations2

题目大意 : 对于一个长度为 \(n\) 的排列，定义其的贡献为对其建笛卡尔树，树上有两个儿子的节点其左右儿子在原排列中的距离之和，给出 \(n, Mod\)，求所有长度为 \(n\) 的排列的贡献之和对 \(Mod\) 取模的值

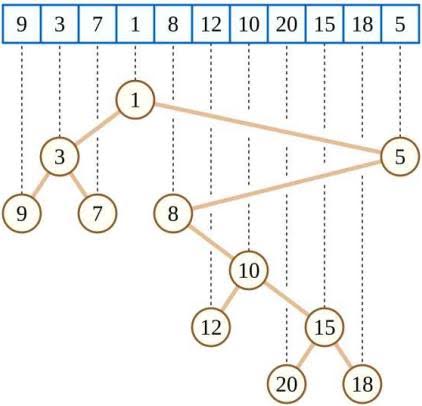
\(1 \leq n \leq 100\)

解题思路 :

考虑一个最暴力的 \(dp\) ，设 \(f[i][j][k]\) 表示区间 \([i, j]\) 的极值在 \(k\) 上的答案

每次的转移的贡献由两部分组成，其一是划分成的左右区间的答案乘上排列数，其二是左右儿子产生的贡献

第一种贡献十分简单，在此不多做讨论，主要考虑第二种贡献

考虑最暴力的转移，枚举左边的极值的位置 \(l\), 和最右边的极值 \(r\) ，那么中间的贡献就是

\(\sum_{l=i}^{k-1}\sum_{k+1}^{j} (k-i-1)! \times(j-k-1)!\times(r - l)\)

观察发现，无论 \(l, r\) 的取值是多少，它的排列数都等同于一个位置固定剩下随便排的方案数

也就是说，排列数只和左右区间的大小有关，和极值的具体位置无关

所以我们可以不必在状态中记极值的位置，直接枚举当且区间的极值是什么然后拿划分成的左右区间转移

再回到之前的转移式子，观察发现只要对这个式子稍加变换就能把 \(\sum\) 符号去掉

首先把排列数提出来 \((k-i-1)! \times(j-k-1)!\times\sum_{l=i}^{k-1}\sum_{k+1}^{j} (r - l)\)

设 $sum(i, j) $ 表示 \(i + (i + 1) +..+ j\) 的和，这个可以 \(O(1)\) 计算，把 \(sum()\) 代入式子得

\((k-i-1)! \times(j-k-1)!\times [sum(k+1, j) \times (k - i) - sum(i, k-1) \times (j-k)]\)

经过基础的推式子之后，我们省去了对极值所在位置的在状态上的记录，并且将枚举左右两个极值位置的 \(\sum\) 消去

所以状态变为 \(f[i][j]\) 表示所有排列在区间 \([i,j]\) 上的答案

转移方程变成了

\(f[i][j] = \sum_{k=i}^{j} C_{j-i}^{k-1}\times \{(f[i][k-1] \times(j-k)!)+(f[k+1][j] \times(k-i)!) + (k-i-1)! \times(j-k-1)!\times [sum(k+1, j) \times (k - i) - sum(i, k-1) \times (j-k)]\}\)

复杂度变成了 \(O(n^3)\)

事实上还可以观察发现，对于大小相同的区间其\(f\)值是一样，可以记\(f_i\) 表示长度为 \(i\) 的区间的答案，枚举其可能的子区间大小转移

这个方程会是一个卷积的形式，所以可以通过 \(FFT\) 来优化复杂度，不过 \(O(n^3)\) 的算法已经可以解决此题，这个算法就不过多讨论了

/*program by mangoyang*/
typedef long long ll;
ll f[1005][1005], g[1005][1005], js[1005], Mod, n, ans;
inline ll C(ll n, ll i){ return f[n][i]; }
inline ll sum(ll l, ll r){ return ((l + r) * (r - l + 1) / 2) % Mod; }
inline ll Pow(ll a, ll b){
	ll ans = 1;
	for(; b; b >>= 1, a = a * a % Mod)
		if(b & 1) ans = ans * a % Mod;
	return ans;
}
int BearPermutations2::getSum(int N, int MOD) {
    n = N, Mod = MOD, ans = 0, js[0] = 1;
    for(int i = 1; i <= n; i++) js[i] = js[i-1] * i % Mod;
    memset(f, 0, sizeof(f)), memset(g, 0, sizeof(g));
    for(int i = 0; i <= n; i++) f[i][0] = 1;
    for(int i = 1; i <= n; i++)
    	for(int j = 1; j <= i; j++) f[i][j] = (f[i-1][j-1] + f[i-1][j]) % Mod;
   	for(int i = n; i >= 1; i--)
   		for(int j = i; j <= n; j++){
   			for(int k = i; k <= j; k++){
   				if(k > i) (g[i][j] += C(j - i, k - i) * g[i][k-1] % Mod * js[j-k] % Mod) %= Mod;
   				if(k < j) (g[i][j] += C(j - i, k - i) * g[k+1][j] % Mod * js[k-i] % Mod) %= Mod;
   				if(k == i || k == j) continue;
   				ll tmp = js[k-i-1] * js[j-k-1] % Mod * C(j - i, k - i) % Mod;
   				ll now = ((sum(k + 1, j) * (k - i) % Mod) - (sum(i, k - 1) * (j - k) % Mod) + Mod) % Mod;
   				g[i][j] = (g[i][j] + now * tmp % Mod) % Mod;
   			}
   		}
   	return g[1][n];
}