LG5024 保卫王国

保卫王国

题目描述

Z 国有\(n\)座城市，\(n - 1\)条双向道路，每条双向道路连接两座城市，且任意两座城市 都能通过若干条道路相互到达。

Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件：

• 一座城市可以驻扎一支军队，也可以不驻扎军队。
• 由道路直接连接的两座城市中至少要有一座城市驻扎军队。
• 在城市里驻扎军队会产生花费，在编号为i的城市中驻扎军队的花费是\(p_i\)。

小 Z 很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小 Z 提出 了\(m\)个要求，每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一 给出回答。具体而言，如果国王提出的第\(j\)个要求能够满足上述驻扎条件（不需要考虑 第 \(j\) 个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。如果 国王提出的第\(j\)个要求无法满足，则需要输出\(-1 (1 ≤ j ≤ m)\)。现在请你来帮助小 Z。

输入输出格式

输入格式：

第 1 行包含两个正整数\(n,m\)和一个字符串\(type\)，分别表示城市数、要求数和数据类型。\(type\)是一个由大写字母 A，B 或 C 和一个数字 1，2，3 组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中 有具体的描述。

第 2 行\(n\)个整数\(p_i\)，表示编号ii的城市中驻扎军队的花费。

接下来\(n - 1\)行，每行两个正整数\(u,v\)，表示有一条\(u\)到\(v\)的双向道路。

接下来\(m\)行，第\(j\)行四个整数\(a,x,b,y(a ≠ b)\))，表示第\(j\)个要求是在城市\(a\)驻扎\(x\)支军队， 在城市\(b\)驻扎\(y\)支军队。其中，\(x\) 、 \(y\) 的取值只有 0 或 1：若 \(x\) 为 0，表示城市 \(a\) 不得驻 扎军队，若 \(x\) 为 1，表示城市 \(a\) 必须驻扎军队；若 \(y\)为 0，表示城市$ b$不得驻扎军队， 若 $y $为 1，表示城市 \(b\) 必须驻扎军队。

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

输出格式：

输出共 \(m\) 行，每行包含 1 个整数，第\(j\)行表示在满足国王第\(j\)个要求时的最小开销， 如果无法满足国王的第\(j\)个要求，则该行输出 -1。

输入输出样例

输入样例#1：

5 3 C3

2 4 1 3 9

1 5

5 2

5 3

3 4

1 0 3 0

2 1 3 1

1 0 5 0

输出样例#1：

12

7

-1

说明

【样例解释】

对于第一个要求，在 4 号和 5 号城市驻扎军队时开销最小。

对于第二个要求，在 1 号、2 号、3 号城市驻扎军队时开销最小。

第三个要求是无法满足的，因为在 1 号、5 号城市都不驻扎军队就意味着由道路直接连 接的两座城市中都没有驻扎军队。

【数据规模与约定】

对于\(100\%\)的数据，\(n,m ≤ 100000,1 ≤ p_i ≤ 100000\)。



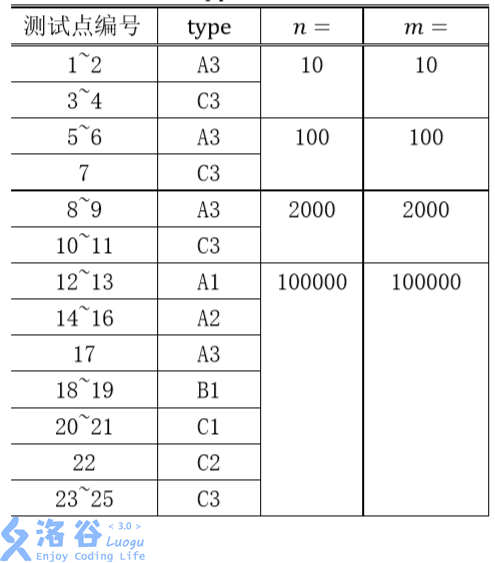
数据类型的含义：

A：城市i与城市i + 1直接相连。

B：任意城市与城市 1 的距离不超过 100（距离定义为最短路径上边的数量），即如果这 棵树以 1 号城市为根，深度不超过 100。

C：在树的形态上无特殊约束。

1：询问时保证a = 1,x = 1，即要求在城市 1 驻军。对b,y没有限制。

2：询问时保证a,b是相邻的（由一条道路直接连通）

3：在询问上无特殊约束。

分析

考虑没有修改时的做法，设\(f[x][1/0]\)表示\(x\)选不选的最小花费，转移：

\[f[x][1]=\sum \min\{f[y][0],f[y][1]\} \\
f[x][0]=\sum f[y][1]
\]

现在有强制取舍，考虑可以把权值减加\(\infty\)来处理（注意这里写成赋值较麻烦），所以要实现的就是一个带点权修改的动态DP。类似的定义除去重儿子的贡献的\(g\)数组。

重定义矩乘运算中的乘法为加法，求和为取min，则转移方程为：

\[\left(
\begin{matrix}
+\infty & g[i][0] \\
g[i][1] & g[i][1]
\end{matrix}
\right)*
\left(
\begin{matrix}
f[i+1][0] \\
f[i+1][1]
\end{matrix}
\right)=
\left(
\begin{matrix}
f[i][0] \\
f[i][1]
\end{matrix}
\right)
\]

注意转移前后\(f\)中的下标位置要一致。并且在叶子节点的时候，转移矩阵里的\(+\infty\)要赋成0，这样才能代表\(f[leaf][0]\)。

时间复杂度\(O(n+m \log^2 n)\)

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
	rg T data=0,w=1;
	rg char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(isdigit(ch))
		data=data*10+ch-'0',ch=getchar();
	return data*w;
}
template<class T>il T read(rg T&x){
	return x=read<T>();
}
typedef long long ll;
using namespace std;

co ll N=1e5+5,INF=1e10;
int n,m,a[N];
int ecnt,adj[N],nxt[2*N],go[2*N];
int fa[N],son[N],sze[N],top[N],idx[N],pos[N],tot,ed[N];
ll f[N][2];
struct matrix{
	ll g[2][2];
	matrix(){for(int i=0;i<2;++i)for(int j=0;j<2;++j)g[i][j]=INF;}
	matrix operator*(co matrix&b)co{
		matrix c;
		for(int i=0;i<2;++i)
			for(int j=0;j<2;++j)
				for(int k=0;k<2;++k)
					c.g[i][j]=min(c.g[i][j],g[i][k]+b.g[k][j]);
		return c;
	}
}val[N],data[4*N];

void add(int u,int v){
	go[++ecnt]=v,nxt[ecnt]=adj[u],adj[u]=ecnt;
}
void init(){
	static int que[N];
	que[1]=1;
	for(int ql=1,qr=1;ql<=qr;++ql)
		for(int u=que[ql],e=adj[u],v;e;e=nxt[e])
			if((v=go[e])!=fa[u])
				fa[v]=u,que[++qr]=v;
	for(int qr=n,u;qr;--qr){
		sze[u=que[qr]]++;
		sze[fa[u]]+=sze[u];
		if(sze[u]>sze[son[fa[u]]]) son[fa[u]]=u;
	}
	for(int ql=1,u;ql<=n;++ql)
		if(!top[u=que[ql]]){
			for(int v=u;v;v=son[v])
				top[v]=u,idx[pos[v]=++tot]=v;
			ed[u]=tot;
		}
	for(int qr=n,u;qr;--qr){
		u=que[qr];
		f[u][1]=a[u];
		for(int e=adj[u],v;e;e=nxt[e])
			if(v=go[e],v!=fa[u]){
				f[u][0]+=f[v][1];
				f[u][1]+=min(f[v][0],f[v][1]);
			}
	}
}

void build(int k,int l,int r){
	if(l==r){
		ll g0=0,g1=a[idx[l]];
		for(int u=idx[l],e=adj[u],v;e;e=nxt[e])
			if((v=go[e])!=fa[u]&&v!=son[u])
				g0+=f[v][1],g1+=min(f[v][0],f[v][1]);
		data[k].g[0][0]=l==ed[top[idx[l]]]?0:INF,data[k].g[0][1]=g0; // edit 2:leaf init to be 0
		data[k].g[1][0]=g1,data[k].g[1][1]=g1;
		val[l]=data[k];
		return;
	}
	int mid=l+r>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	data[k]=data[k<<1]*data[k<<1|1];
}
void change(int k,int l,int r,int p){
	if(l==r){
		data[k]=val[l];
		return;
	}
	int mid=l+r>>1;
	if(p<=mid) change(k<<1,l,mid,p);
	else change(k<<1|1,mid+1,r,p);
	data[k]=data[k<<1]*data[k<<1|1];
}
matrix query(int k,int l,int r,int ql,int qr){
	if(ql<=l&&r<=qr) return data[k];
	int mid=l+r>>1;
	if(qr<=mid) return query(k<<1,l,mid,ql,qr);
	if(ql>mid) return query(k<<1|1,mid+1,r,ql,qr);
	return query(k<<1,l,mid,ql,qr)*query(k<<1|1,mid+1,r,ql,qr);
}
matrix ask(int u){
	return query(1,1,n,pos[top[u]],ed[top[u]]);
}
void path_change(int u,ll x){
	val[pos[u]].g[1][0]+=x,val[pos[u]].g[1][1]+=x; // edit 1:+-INF
	matrix od,nw;
	while(u){
		od=ask(top[u]);
		change(1,1,n,pos[u]);
		nw=ask(top[u]);
		u=fa[top[u]];
		val[pos[u]].g[0][1]+=nw.g[1][0]-od.g[1][0];
		val[pos[u]].g[1][0]+=min(nw.g[0][0],nw.g[1][0])-min(od.g[0][0],od.g[1][0]);
		val[pos[u]].g[1][1]=val[pos[u]].g[1][0];
	}
}
int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	read(n),read(m),read<int>();
	for(int i=1;i<=n;++i) read(a[i]);
	for(int i=1,u,v;i<n;++i)
		read(u),read(v),add(u,v),add(v,u);
	init();
	build(1,1,n);
	matrix t;
	for(int a,x,b,y;m--;){
		read(a),read(x),read(b),read(y);
		if(!x&&!y&&(fa[a]==b||fa[b]==a)) {puts("-1");continue;}
		path_change(a,x?-INF:INF),path_change(b,y?-INF:INF);
		t=ask(1);
		printf("%lld\n",min(t.g[0][0],t.g[1][0])-(x?-INF:0)-(y?-INF:0));
		path_change(a,x?INF:-INF),path_change(b,y?INF:-INF);
	}
	return 0;
}

后记

这题，我在考场上看都没看……L巨说这题暴力有44分，失策了。