Numpy 练习题

1. 使用循环和向量化两种不同的方法来计算 100 以内的质数之和。

先定义个判断质数的函数。ps：纯手工打造，原生态，哈哈。

def checkprime(x):
    if x<=1:
        return False;
    prime=True;
    for i in range(2 , 1+x/2):
        if x%i == 0:
            prime = False;
            break;
    return prime;

使用循环方法来计算 100 以内的质数之和。

def sumprimebyiter(n=100):
    primesum=0
    for i in range(1, n+1):
        if( True == checkprime(i)):
            primesum += i
    return primesum

%timeit sumprimebyiter(100)

10000 loops, best of 3: 138 µs per loop

使用向量化的方法来计算 100 以内的质数。ps：怎么将判断质数的函数应用到向量中的每一个元素，可是花了好几分钟来寻找，终于发现 map 可以实现这个功能。后来又发现 np.vectorize 也可以实现同样功能。

import numpy as np
def sumprimebyarr(n=100):
    a = np.arange(1,n+1)
    # return sum(a[np.array(map(CheckPrime, a))]) # 此处是之前用 Python 自带的 map 把函数应用到向量的每个元素
    check_prime_vec = np.vectorize(CheckPrime) # 此处代码用到了 np.vectorize，可以把外置函数应用到向量的每个元素
    return np.sum(a[check_prime_vec(a)])

%timeit sumprimebyarr(100)

10000 loops, best of 3: 204 µs per loop

上面两种方法都使用魔术函数 %timeit 计算了执行时间，意外的是，向量化的方法竟然没有循环快，一定是哪儿不对，待我好好检查下，再补充该题答案。

2. 模拟一个醉汉在二维空间上的随机漫步。

先试试一维空间上的随机漫步。既然本周学了 Numpy，这里就直接上 np.random 了。

%pylab inline

Populating the interactive namespace from numpy and matplotlib

nsteps = 1000
draws = np.random.randint(-1,2,size=nsteps)
walk = draws.cumsum()
plot(walk)

[<matplotlib.lines.Line2D at 0x7f52c3534250>]

再来看下二维的。

nsteps = 1000
draws = np.random.randint(-1,2,size=(2,nsteps))
walks = draws.cumsum(1)
plot(walks[0,:],walks[1,:])

[<matplotlib.lines.Line2D at 0x7f52c34cf3d0>]

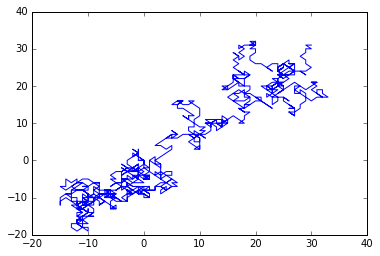
先生成 1000 个随机漫步方向，方向是从 {-1, 0, 1} 中随机挑两个值（两个值也可相等）作为移动方向，所以每次移动有 3×3=9 种选择，初始位置也是 9 种选择，cumsum 函数是将每次的移动累加，最后通过 plot 画出来。

代码调通之前，我都没想到代码能这么少。Python 还是好用，这要是用 C++ 写，得多少代码啊。

3. 使用梯形法计算一个二次函数的数值积分。

梯形法计算数值积分，就是把自变量分成无数小段，每一小段的面积用一个梯形面积近似，当小段的个数无限多，小段的长度无限小时，所有的小梯形面积加起来，就近似等于该函数的数值积分。如下图所示：

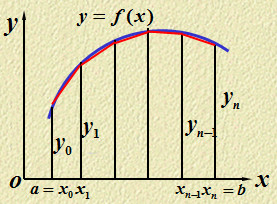
原理很简单，代码也很简单：

import numpy as np
def CompIntegralbyladder(func,x0,x1):
    wholearea = 0
    step = 0.1
    for i in np.arange(x0, x1, step):
        wholearea += (func(i)+func(i+step))*step/2; # Compute the Trapezoidal area
    return wholearea;

该函数可以计算任意函数的积分。函数写好了，都分隔成长度为 0.1 的小区间。先来测试下指数函数的积分。

\[\int_{1}^{4} e^{x}dx
\]

CompIntegralbyladder(np.exp,1,4)

51.923094224367127

来看下正确答案。注意指数函数的不定积分还是指数函数本身。

from sympy.interactive import printing
printing.init_printing(use_latex=True)

\[\int_{1}^{4}e^{x}=e^{4}-e^{1}
\]

np.exp(4)-np.exp(1)

51.879868204685188

附上指数函数的图形。

%pylab inline

Populating the interactive namespace from numpy and matplotlib

import numpy as np
x = np.linspace(-5, 5, num = 100)
y = np.exp(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.show()

再看看计算个二次函数的积分。随便写个二次函数。

\[2x^{2}+3x+4
\]

def Quadratic(x):
    return 2*x**2 + 3*x + 4

先来看看这个函数的图形。

import numpy as np
x = np.linspace(-5, 5, num = 100)
y = Quadratic(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.show()

我们就计算该二次函数从 -5 到 5 的积分吧。

\[\int_{-5}^{5}2x^{2}+3x+4 dx
\]

CompIntegralbyladder(Quadratic,-5,5)

206.69999999999825

下面来计算下正确的积分值。

因为：

\[\int2x^{2}+3x+4dx=\frac{2}{3}x^3+\frac{3}{2}x^2+4x
\]

所以：

\[\int_{-5}^{5}2x^{2}+3x+4dx=[\frac{2}{3}x^3+\frac{3}{2}x^2+4x]_{-5}^{5}
\]

def Integral(x):
    return (2*x**3)/3 + (3*x**2)/2 + 4*x

Integral(5)-Integral(-5)

207

可见，梯形法计算积分还是比较准确的。