20172305 2018-2019-1 《Java软件结构与数据结构》第六周学习总结

20172305 2018-2019-1 《Java软件结构与数据结构》第六周学习总结

教材学习内容总结

本周内容主要为书第十章内容：

• 树(一种非线性结构，其中的元素被组织成一个层次结构)

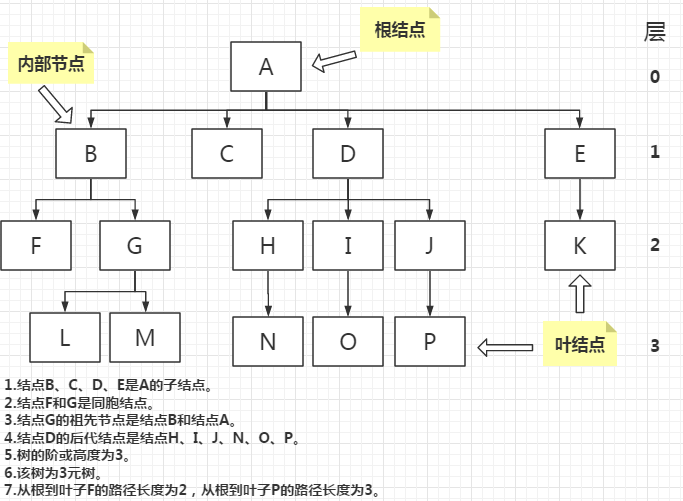
  • 结点：树中的一个位置。
  • 边：树中两个结点的连接。
  • 根结点：就是指位于该树顶层的唯一结点。一棵树只有一个根结点，根结点没有父节点。
  • 子结点：一个树中较低层的结点是上一层结点的子结点。位于树中当前结点下面的结点，并由边与之直接连接。
  • 同胞结点：属于同一结点的子结点。
  • 叶结点：没有任何子结点的结点。
  • 内部节点：一个至少有一个子结点的非根节点。
  • 祖先节点：位于当前结点以上的结点。
  • 后代结点：位于当前结点一下的结点。
  • 路径长度：通过计算从根到该结点所必须越过的边数目。
  • 高度：从根到叶子之间的最远路径的长度。
  • 阶(度)：树中任一结点可以具有的最大子结点的数目。
    
    

• 树的分类：

  • 二叉树：结点最多具有两个孩子的树。
  • 完全树：如果某树是平衡的，且底层所有叶子都位于树的左边，则认为该树是完全的。
    
    
  • 满树：如果一颗n元树的所有叶子都位于同一层且每一结点要么是一片叶子，要么是正好具有n个孩子。
  • 完全二叉树：在每个K层上都有2^k个结点，最后一层除外，在最后一层中的结点必须是在最左边结点。/ 在每个k层上都具有2^k个结点，最后一层除外，在最后一层中的结点必须是最左的。
  • 平衡树与非平衡树：
    
    

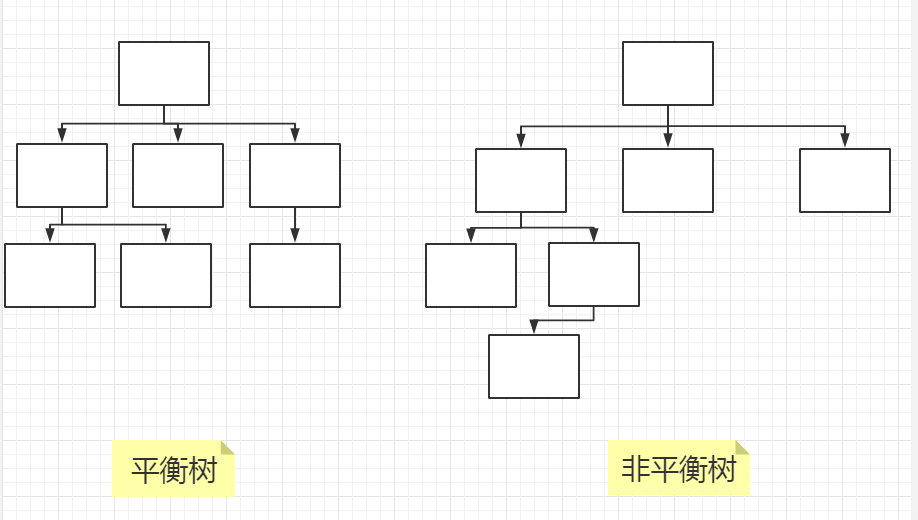
• 含有m个元素的平衡n元树具有的高度为lognm。

• 树的遍历：

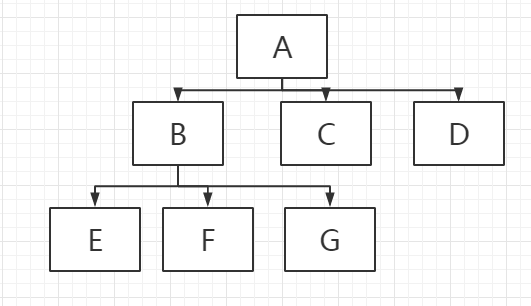
  • 前序遍历：从根结点开始，访问每一个结点及其孩子。(A->B->D->E->C)
  • 中序遍历：从根结点开始，访问结点的左侧孩子，然后是该结点，再然后是任何剩余的结点。(D->B->E->A->C)
  • 后序遍历：从根结点开始，访问结点的孩子，然后是该结点。(D->E->B->C->A)
  • 层序遍历：从根节点开始，访问每一层的所有结点，一次一层。(A->B->C->D->E)
    
    

• 对于任何存储在数组位置n处的元素而言，该元素的左结点将存储在位置2n+1处，该元素的右结点将存储在位置2(n+1)处。

• 模拟链接策略允许连续分配数组位置而不用考虑该树的完全性。

• 二叉树--表达式树表达式树的及其内部结点包含着操作，且所有叶子也包含着操作数。对操作树的求值是从下往上的。

• 二叉树--决策树(背部疼痛诊断器)决策树的结点表示决策点，其子结点表示在该决策点的可选项。决策树的叶结点表示可能的判断，这些推断是根据决策结果得出的。

教材学习中的问题和解决过程

• 问题1:完全二叉树和满二叉树的区别？
• 问题1解决方案：满二叉树是完全二叉树的一种特殊。故满二叉树肯定是完全二叉树，完全二叉树不一定是满二叉树。是因为完全二叉树倒数第二层的结点可以有一个子结点(当然是左侧节点)，可以有两个结点，也可以无子结点。而满二叉树则要最后一层的结点数必须为最大的，这就要求倒数第二层的每个结点其子结点必须是两个 即为满二叉树的倒数第二层的结点无叶结点的情况。

• 满二叉树是指除最后一层外，每一层上的所有结点都有两个子结点。
  • 如果一颗满二叉树的深度为d，最大层数为k
  • 它的叶子数是: 2^d
  • 第k层的节点数是: 2^(k-1)
  • 总节点数是: 2^k-1 => (1 + 2 + 4 + 8 ··· + 2^(k-1)的和),其总节点数一定是奇数。

• 完全二叉树是指除最后一层外，每一层上的结点数均达到最大值；在最后一层上只缺少右边的若干结点。
• 完全二叉树的判断方法：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
• 完全二叉树的特点是:
  • 只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现。
  • 对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。

• 问题2：书上表达式树printTree()代码如何理解?
• 问题2解决方案：PostfixEvaluator类的getTree()内容是(treeStack.peek()).printTree()是把树的形式从栈treeStack的顶部返回出来，再调用Expreesion类中的printTree方法(最恶心的部分)，就成一棵树了。

public String printTree() {
		UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes = new ArrayUnorderedList<BinaryTreeNode<ExpressionTreeOp>>();
		UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>();

		BinaryTreeNode<ExpressionTreeOp> current;
		String result = "";
		int printDepth = this.getHeight();
		int possibleNodes = (int) Math.pow(2, printDepth + 1);
		int countNodes = 0;

		nodes.addToRear(root);
		Integer currentLevel = 0;
		Integer previousLevel = -1;
		levelList.addToRear(currentLevel);

		while (countNodes < possibleNodes) {
			countNodes = countNodes + 1;
			current = nodes.removeFirst();
			currentLevel = levelList.removeFirst();
			if (currentLevel > previousLevel) {
				result = result + "\n\n";
				previousLevel = currentLevel;
				for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
					result = result + " ";
			} else {
				for (int i = 0; i < ((Math.pow(2,
						(printDepth - currentLevel + 1)) - 1)); i++) {
					result = result + " ";
				}
			}
			if (current != null) {
				result = result + (current.getElement()).toString();
				nodes.addToRear(current.getLeft());
				levelList.addToRear(currentLevel + 1);
				nodes.addToRear(current.getRight());
				levelList.addToRear(currentLevel + 1);
			} else {
				nodes.addToRear(null);
				levelList.addToRear(currentLevel + 1);
				nodes.addToRear(null);
				levelList.addToRear(currentLevel + 1);
				result = result + " ";
			}

		}
		return result;
	}

• 代码中的两个无序列表，一个存放的是BinaryTreeNode类型，就是表达式树的每一个结点；另一个存放的是Integer类型，用来与之前的无序列表对应，每往无序列表中存放一个结点，就在另一个无序列表中存入对应的层数。

• 代码中的几个整形变量，printDepth输出的是高度(从零开始的,实际树是四层就输出三层，根结点所在层数为0)，possibleNode通过调用Math的静态方法pow()来算树的最大结点数。其中Math.pow(2, printDepth + 1)按照老师讲的应该是2^printDepth - 1，但是算法给出的是2^(printDepth+1),实际上我们调用的getHeight()方法会从第零行开始计算，而在实际上是从一层开始的，这样的话就需要把再加1。而尾部的减1，没有再此体现。在后面的while循环的条件来看，记录输出结点数量的变量 < possibleNodes,这样的话就可以使得记录输出结点数量的变量最大情况等于possibleNodes - 1，这样就是最大结点数。还有三个整形变量，一个是countNodes，是记录输出的结点数目的；一个是currentLevel记录当前结点所在的层；一个是previousLevel记录的是当前结点的前一层。

• 过程：调出根结点A，此时对应的层数是-1，存放到对应的无序列表中。此时，countNodes(输出的结点数目)的初始值为0，
  
  开始第一次进入循环，countNodes加1，调出无序列表中的结点。此时根结点的层数为0，前一层为-1，进入第一个条件，换行previousLevel等于currentLevel(两个变量值都为0)，然后输出根节点的内容，跳出第一个条件。进入第二个条件，将根结点的左子结点添加到无序列表的尾部，对应的记录层数的无序列表添加数字1，再将根结点的右子结点添加到无序列表，对应记录层数的无序列表添加数字1，第一次循环结束。
  
  进行第二次循环，此时调出根结点的左子结点的内容和左子结点的层数，层数为1，前一层是0，进入第一个条件，换行previousLevel等于currentLevel(两个变量值都为1)，然后输出左子结点的内容，跳出第一个条件。进入第二个条件，往里面插入左结点的子结点，此时存放节点的无序列表内有和输出的左结点同一层的右结点，和左结点的两个子结点，先左节点后右结点，对应的层数应该均为3，第二次循环结束。
  
  进行第三次循环，此时调出的是根结点的右子结点和层数，层数和左结点相同也为1，进入第一个条件(else部分)，取消了换行和previousLevel等于currentLevel，这样的话就和左子结点同行输出，把根结点的两个子结点都输出来了。跳出第一个条件，再将右结点的两个子结点和对应的层数放到无序列表，其中两个子结点的层数均为2，第三次循环结束。
  
  进行第四次循环，此时调出的根结点的左结点的左子结点，此时对应的层数是2。此时的previousLevel为1，currentLevel为2，进入第一个条件的if部分，进行换行并输出该结点的内容，跳出第一个条件，因为该结点为空，所以进入第二个条件的else部分，会默认添加该结点的两个子结点，但是子结点的内容为空，即插入到无序列表的内容为空，但是层数会进行增加，第四次循环结束。
  
  重复进行上述循环(已经调用整个部分的相关代码，股不在叙述操作)，最后达到循环超过该树的总结点数即possibleNodes跳出循环，输出result就是整个树了。

• 问题3：背部疼痛诊断器的诊断过程总是回答完一个yes之后就蹦了？

• 问题3的解决方案：针对这个问题，刚开始只是敲上去而没有真正去运行。后来听同学的运行之后有问题，这才去运行，结果真有问题。不能转化为String，很神奇！！！明明在txt文件内已经有了内容的，就是转换不成String。刚开始以为是读文件的部分有问题，但是没找到问题，通过单步调试也只是在最后一步有问题。所以，很疑惑！更关键的是这个同样的代码在别的电脑上会有运行成功的。相同的一段代码，我的电脑上会提醒有个判断总是false，而别的上面就没有。很迷...通过侯泽洋的帮助，是我们在获得左结点或是右结点时候只是调出其中的内容，该节点的子结点根本没有调出来导致的，完全就是个只有该结点的一个树了，在LinkedBinaryTree中添加几句就可以结点的子结点都调出来了。

  • 始终有问题的部分：

  

  • 错误图片：
    
    
  • 王文彬提供的代码(修改位置)：

  

  • 侯泽洋提供的代码(修改位置)：

  

  

  

代码学习中的问题和解决过程

• 问题1：链表实现的二叉树的toSring代码如何编写？

• 问题1的解决方案：return super.toString();会出现带有包名的哈希码，没有正常的输出内容。准备重新书写的输出的代码的时候，发现如果输出的话就需要用递归的方法，来从树中一层一层的从左往右的按顺序输出。但是如果用到了递归的话，注定用String类型的变量输出不出来(因为要进行一个叠加的过程，而设置变量的话也不能在此方法下进行输出。需要像之前的那个归并排序和快速排序一样，一个进行递归的主要方法，另一个调用该递归方法，来达到代码的实现。)图过时用递归来实现的话，就可以运用不同的遍历方式。通过书上代码--表达式树的输出树状形式，就直接搬过来实现toString方法(相关代码分析在教材分析总结)。

  • 产生带包名哈希码：
  • 前序输出：从根结点开始，访问每一个结点及其子结点。所以，先调出根结点的内容，然后从左结点开始调出至右结点的内容。
  • 中序输出：从根结点开始，先访问结点的左子结点的内容，在调出该结点的内容，再访问结点的右子结点的内容。
  • 后序输出：从根结点开始，先访问该结点的子结点的内容，在退回到结点的内容。
  • 层序输出：从根节点开始，每一层的从左到右的进行输出。

  

  • 树状输出(借鉴表达式树的形式)：

  

• 问题2：表达式树的输出为什么总是输出不对？

• 问题2解决方案：书上表达式树的代码在进行树的输出时候，总会输出的稀乱稀乱的一堆，代码也没有爆红。第一次通过单步调试发现，是自己的getHeight()方法的方法体没有写，导致输出的结果总是0。还要自己修改getHeight()...悲惨自行补了相关代码，先判断树是不是空的，不空的话通过PP10.3做的代码，进行判断是否是叶结点进行循环遍历，在遍历的过程中进行计数。但是在输出树的情况下就是缺最后一行，通过尝试对一个已知高度的树调用getHeight()方法时，在输出的时候发现会比实际高度少1，所以在计数变量的初始值从0改为1尝试一下，结果就完整了。

  • 第一次修改：
    
    
  • 第二次修改：
    
    
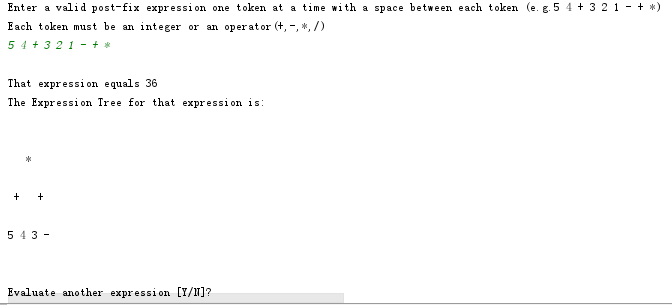
  • 第三次修改：
    
    

• 问题3：removeRightSubtree、removeAllElement和contains方法

• 问题3解决方案：

  • 针对removeRightSubtree方法觉得需要先进行遍历，每遍历一个再删除一个，直到完成任务。后来想想觉得好麻烦，还要进行迭代。想出一个简单粗暴的方法，就是已经确定删除右枝杈了，那么就直接把节点的右侧枝杈直接改为null就可以了，根本不用管其内容就是删。但是，做出的第一个版本，是删除根结点的右侧，那么如果想删除某个节点的右侧，这样的话方法就不会起作用。所以，改进了此方法以实现可以删除某一个节点的右子结点。
  • 针对removeAllElement方法，因为实现前一个方法时简单粗暴，而此方法和之前的有一定的类似，所以直接就重新定义一个BinaryTreeNode类的根结点，让其为零，再使这个结点替代之前有内容的树就可以了。
  • 针对contains方法，这个方法是判断指定目标是否在该树上。因为之前有书上的find方法作支撑，就通过该方法查找出是否有指定元素，如果就输出true，没有就false。

代码托管

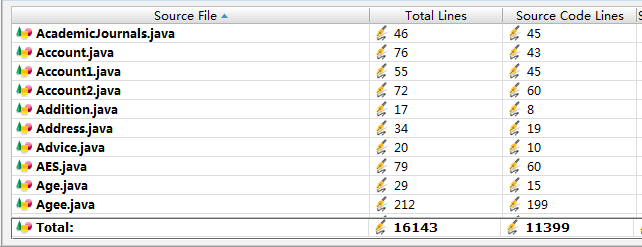
上周考试错题总结

无错题，终于不用错题总结了...

结对与互评

点评(王禹涵)

• 博客中值得学习的或问题：
  • 背景图很好看，但是截图内容看得不是很清晰。问题2的代码也进行了注释，是我应该学习的地方。
• 代码中值得学习的或问题：
  • 代码图片也是看的不清晰，问题提的很好，问题2出现的是哈希码，建议可以尝试这用四种遍历顺序输出，或是像树那样输出。
• 基于评分标准，我给本博客打分：8分。
  • 得分情况如下：
  • 正确使用Markdown语法（加1分）
  • 模板中的要素齐全（加1分）
  • 教材学习中的问题和解决过程, 两个问题加2分
  • 代码调试中的问题和解决过程, 两个问题加2分
  • 感想，体会不假大空的加1分
  • 点评认真，能指出博客和代码中的问题的加1分

点评(方艺雯)

• 博客中值得学习的或问题：
  • 图片特别细致清晰，而且针对实现树的策略写的很详细，针对printTree方法可以更进一步的描述运算过程。
• 代码中值得学习的或问题：
  • 代码问题记录详细，第二个问题我也遇到过。建议在插图的时候可以添加多一点的文字描述，没有什么大问题，写的很棒棒。
• 基于评分标准，我给本博客打分：10分。
• 得分情况如下：
  • 正确使用Markdown语法（加1分）
  • 模板中的要素齐全（加1分）
  • 教材学习中的问题和解决过程, 二个问题加2分
  • 代码调试中的问题和解决过程, 四个问题加4分
  • 感想，体会不假大空的加1分
  • 点评认真，能指出博客和代码中的问题的加1分

互评对象

• 本周结对学习情况
  
  20172314方艺雯
  
  20172323王禹涵

• 结对学习内容：树

感悟

第十章的树学起来很费劲，完全的一个接着一个，没有顺序，没有结构的(二叉树还好点)。课后的代码相对简单，但是书上的示例代码写的比课后代码还麻烦。非常感谢侯泽洋的帮助，帮助我更好的理解树的相关知识，有些代码的问题是在帮助下完成的，这也显示出我的不足，没有更好的掌握知识，逻辑的相关内容只有自己弄懂才行，别人的帮助只是辅助的。起初还感觉前面代码相对简单，但那是到了树的部分真是欲哭无泪的感觉。只能再好好的学习学习再学习了。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	15/15
第二周	703/703	1/2	20/35
第三周	762/1465	1/3	20/55
第四周	2073/3538	1/4	40/95
第五周	981/4519	2/6	40/135
第六周	1088/5607	2/8	50/185

参考资料

• 完全二叉树
• 满二叉树