AStar算法()

　　把网上的AStar算法的论述自己实现了一遍，一开始只是最基础的实现。当然，现在AStar算法已经演变出了各种优化的版本，这篇也会基于各种优化不断的更新。

　　如果对算法不熟悉可以看下Stanford的这篇文章，我觉得是讲解的十分仔细的了：http://theory.stanford.edu/~amitp/GameProgramming/，也附上国内的翻译：http://blog.csdn.net/coutamg/article/details/53923717

　　讲讲我对上面这篇文章的理解：

　　（1）AStar算法的核心就在于这个公式了f(n) = g(n) + h(n)，算法的效果如何也都取决于这个公式。就如文章中说的，g(n)可以看做从start到current所花费的cost，h(n)从current到end的花费。

　　　　很多人会直接将这两个当做距离来计算，这是在忽略地形等条件影响下最简单的模型。对于每一步，我们可以确定g(n)的准确值，但是h(n)很难预估正确的值（特别是在复杂且大型的场景中）。文章中也提供了几种解决方案比如waypoint等。

　　（2）算法维护着两张表openlist和closelist，openlist初始化时将start加入。

　　　　在循环寻找路径时，将openlist中优先级最高的元素取出，移入closelist中，表示该点已经“探测”过。对该点的周围N个neighbor进行检测，符合条件将其加入openlist中，并对openlist进行优先级排序。

　　既然是对基础的简单理解，就不多说直接贴上代码：

 using System.Collections;
 using System.Collections.Generic;
 using UnityEngine;

 public class AStar  {

     public enum POINT_TYPE
     {
         normal,
         obstacle,
     }

     public class POINT:System.IComparable
     {
         float _gValue, _hValue;
         public float gValue
         {
             get
             {
                 return _gValue;
             }
             set
             {
                 _gValue = value;
                 fValue = AStar.GetFValue(pos,gValue,hValue);
             }
         }

         public float hValue
         {
             get
             {
                 return _hValue;
             }
             set
             {
                 _hValue = value;
                 fValue = AStar.GetFValue(pos, gValue, hValue);
             }
         }
         public float fValue
         {
             get;
             private set;
         }
         public Vector2 pos, parent;
         public POINT_TYPE type;

         public int CompareTo(object obj)
         {
             POINT pt = obj as POINT;
             if (fValue < pt.fValue)
                 return -;
             else if (fValue == pt.fValue)
                 return ;
             else
                 return ;
         }

     }

     public Dictionary<Vector2, POINT> points = new Dictionary<Vector2, POINT>();
     public static Vector2 startPt, endPt;

     public List<POINT> openList = new List<POINT>();
     public List<POINT> closeList = new List<POINT>();

     public bool finish = false;

     public static float GetFValue(Vector2 pt,float gValue,float hValue)
     {
         Vector2 vec1 = pt - startPt;
         Vector2 vec2 = endPt - startPt;
         float fac = Vector3.Cross(new Vector3(vec1.x, vec1.y, ), new Vector3(vec2.x, vec2.y, )).normalized.z >  ? 0.01f : -0.01f;
         return gValue + 2f * hValue + fac;
     }

     float GetManhattanDistance(Vector2 pos1, Vector2 pos2)
     {
         return Mathf.Abs(pos1.x - pos2.x) + Mathf.Abs(pos1.y - pos2.y);
     }

     List<POINT> GetNeighbours(Vector2 pt)
     {
         List<POINT> neighbouts = new List<POINT>();
         if (points.ContainsKey(new Vector2(pt.x - , pt.y)))
             neighbouts.Add(points[new Vector2(pt.x - , pt.y)]);
         if (points.ContainsKey(new Vector2(pt.x + , pt.y)))
             neighbouts.Add(points[new Vector2(pt.x + , pt.y)]);
         if (points.ContainsKey(new Vector2(pt.x, pt.y +)))
             neighbouts.Add(points[new Vector2(pt.x, pt.y +)]);
         if (points.ContainsKey(new Vector2(pt.x, pt.y - )))
             neighbouts.Add(points[new Vector2(pt.x, pt.y - )]);
         return neighbouts;
     }

     public void Init(List<POINT> pts,Vector2 start,Vector2 end)
     {
         foreach (POINT pt in pts)
         {
             points.Add(pt.pos, pt);
         }

         startPt = start;
         endPt = end;

         points[startPt].parent = start;
         points[startPt].gValue = ;
         points[startPt].hValue = Mathf.Abs(startPt.x - endPt.x) + Mathf.Abs(startPt.y - endPt.y);

         openList.Add(points[startPt]);

         finish = false;
     }

     public void StepNext()
     {
         if (finish)
             return;

         POINT current = openList[];
         openList.Remove(current);
         closeList.Add(current);
         if (current.pos == endPt)
         {
             finish = true;
             return;
         }

         List<POINT> neighbours = GetNeighbours(current.pos);
         for (int i = ; i < neighbours.Count; i++)
         {
             if (neighbours[i].type == POINT_TYPE.obstacle || closeList.Contains(neighbours[i]))
                 continue;

             bool needSort = false;
             float gValue =GetManhattanDistance(neighbours[i].pos,startPt);
             float hValue = GetManhattanDistance(neighbours[i].pos,endPt);
             float fValue = AStar.GetFValue(neighbours[i].pos,gValue,hValue);

             if (openList.Contains(neighbours[i]))
             {
                 if (neighbours[i].fValue > fValue)
                 {
                     neighbours[i].gValue = gValue;
                     neighbours[i].hValue = hValue;
                     needSort = true;
                 }
             }
             else
             {
                 neighbours[i].gValue = gValue;
                 neighbours[i].hValue = hValue;
                 neighbours[i].parent = current.pos;
                 openList.Add(neighbours[i]);
                 needSort = true;
             }

             if (needSort)
                 openList.Sort();
         }

     }

 }

　　简单的标注这几行：

　　49-58 ：继承于IComparable接口类，并且重写了CompareTo方法。这样就可以利用List<T>.Sort()来排序了。在CompareTo方法中，当fValue相等时，hValue值小具有更高的priority。关于fValue相同的情况在论文中有阐述。

　　71-77：根据g(n),h(n)计算f(n)。上面说的算法的核心公式是f(n) = g(n) + h(n)，但是很多时候这样简单的相加并不能适应各种复杂的情况。考虑这样一种情况：

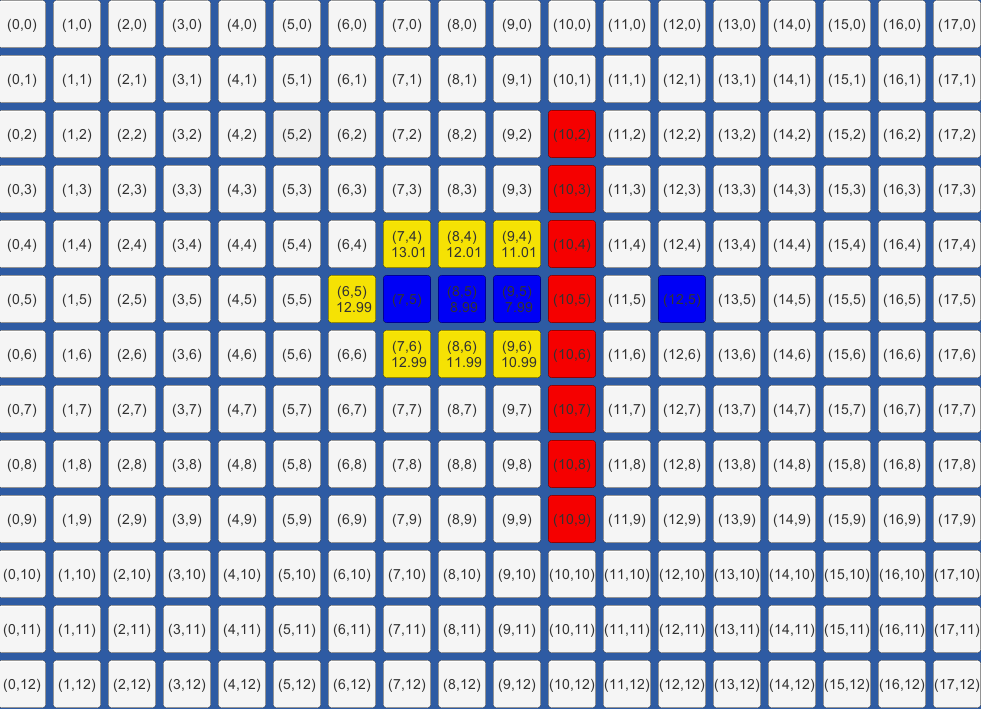
（请忽略这张图中坐标下的数值（f值），并不与代码相符）

　　蓝色为当前探测的点，黄色为待探测的点。若用公式f(n) = g(n) + h(n)此时有两种相等（f和h都相同）的情况，这样将增大计算的消耗。这里简单的用了cross函数使相等时总是能选择某一侧作为偏向。

　　138-139：g和h的值分别为n点到start和end点的曼哈顿距离（x，y轴上距离相加），这里其实只是近似值，并且g的值其实来说并不准确。上文说道g值对于每一步的计算来说都是可以确定的。在本例中暂且这样，下一例中改进。

　　来看一下算法的效果：

　　

　　第一张图从（0,10）到（14,2），第二张图从（0,12）到（14,2）。绿色为算法最终输出的路径，黄色与蓝色为检测的范围。

　　而在实现过程中也法线了g和h对算法的影响。当g>>h时，算法偏向于全方位的检测，当h>>g时，算法偏向于向end点方向检测。