关于PCA降维中遇到的python问题小结

由于论文需要，开始逐渐的学习CNN关于文本抽取的问题，由于语言功底不好，所以在学习中难免会有很多函数不会用的情况.....￣へ￣

主要是我自己的原因，但是我更多的把语言当成是一个工具，需要的时候查找就行~~~~但是这也仅限于搬砖的时候，大多数时候如果要自己写代码，这个还是行不通的。

简单的说一下在PCA，第一次接触这个名词还是在学习有关CNN算法时，一篇博客提到的数据输入层中，数据简单处理的几种方法之一，有提到PCA降维，因为论文需要CNN做一些相关的工作，想做一篇综述类文章，所以思路大概是这样：CNN处理文本历史，CNN处理文本的概述，基本方法，常用框架，具体方法，方法优劣确定，未来研究趋势。

在查看相关常用框架的时候，才发现还有很多没有学过，(ｷ｀ﾟДﾟ´)!!，于是乎，抓紧吧~

PCA（Principal Component Analysis）主成分分析法

在数据处理中，经常会遇到特征维度比样本数量多得多的情况，如果拿到实际工程中去跑，效果不一定好。一是因为冗余的特征会带来一些噪音，影响计算的结果；二是因为无关的特征会加大计算量，耗费时间和资源。所以我们通常会对数据重新变换一下，再跑模型。数据变换的目的不仅仅是降维，还可以消除特征之间的相关性，并发现一些潜在的特征变量。

目的：

PCA是一种在尽可能减少信息损失的情况下找到某种方式降低数据的维度的方法。通常来说，我们期望得到的结果，是把原始数据的特征空间（n个d维样本）投影到一个小一点的子空间里去，并尽可能表达的很好（就是说损失信息最少）。常见的应用在于模式识别中，我们可以通过减少特征空间的维度，抽取子空间的数据来最好的表达我们的数据，从而减少参数估计的误差。注意，主成分分析通常会得到协方差矩阵和相关矩阵。这些矩阵可以通过原始数据计算出来。协方差矩阵包含平方和与向量积的和。相关矩阵与协方差矩阵类似，但是第一个变量，也就是第一列，是标准化后的数据。如果变量之间的方差很大，或者变量的量纲不统一，我们必须先标准化再进行主成分分析。（这里引用了一个大哥的文档，写的真的很漂亮，https://www.cnblogs.com/charlotte77/p/5625984.html）

简单介绍一下，详细的可以看这篇博客，关于PCA降维的方法什么的都在里面，我主要在学习这篇的时候关于语言方面有些小障碍，所以能看懂上面，我这也就基本不用看了~

在第一个问题中：

mu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])

np.random.multivariate_normal(mu_vec1, cov_mat1, 20).T

#def multivariate_normal(mean, cov, size=None, check_valid=None, tol=None)

这段代码中，开始的时候对语法掌握不熟悉，定义部分在注释展示出了，主要的目的是生成随机数组，mean和cov是必须填写的参数，mean为一维数组，cov为协方差矩阵，size为生成随机数组的时候，具体的长度，比如size=20，则第一行元素就一共有20个；check_valid主要是为了检验是否为协方差矩阵，有三种写法：

warn，raise以及ignore。当使用warn作为传入的参数时，如果cov不是半正定的程序会输出警告但仍旧会得到结果；当使用raise作为传入的参数时，如果cov不是半正定的程序会报错且不会计算出结果；当使用ignore时忽略这个问题即无论cov是否为半正定的都会计算出结果。3种情况的console打印结果如下：

使用warn时：

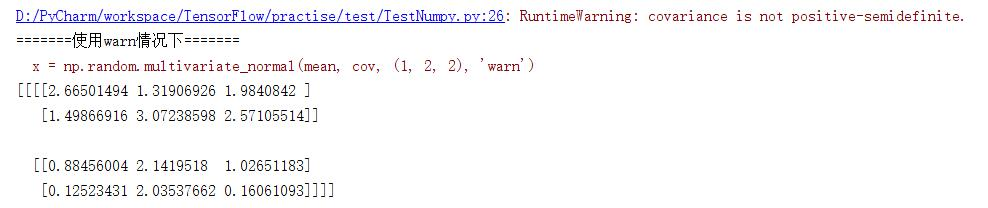
使用raise时：

使用ignore时：

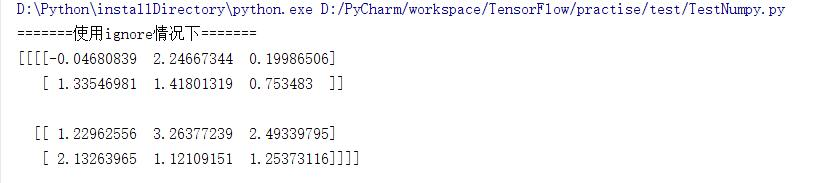
tol：检查协方差矩阵奇异值时的公差，float类型。

这个问题算是解决了~下一个：

class1_sample[0,:]和class1_sample[：,0]

X[:,0]是numpy中数组的一种写法，表示对一个二维数组，取该二维数组第一维中的所有数据，第二维中取第0个数据，直观来说，X[:,0]就是取所有行的第0个数据, X[:,1] 就是取所有行的第1个数据。

import numpy as np

X = np.array([[0, 1], [2, 3], [4, 5], [6, 7], [8, 9], [10, 11], [12, 13], [14, 15], [16, 17], [18, 19]])

print(X[:, 0])

为例

X[:, 0]输出则为，[0,2,4,6,8,10,12,14,16,18]

X[:, 1]输出则为，[1,3,5,7,9,11,13,15,17,19]

X[0, :]输出则为，[0,1]

X[1, :]输出则为，[2,3]

其中还有一个为X[:,  m:n]，即取所有数据的第m到n-1列数据，含左不含右

例：输出X数组中所有行第1到2列数据

1. X = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11],[12,13,14],[15,16,17],[18,19,20]])
2. print X[:,1:3]

结果为：

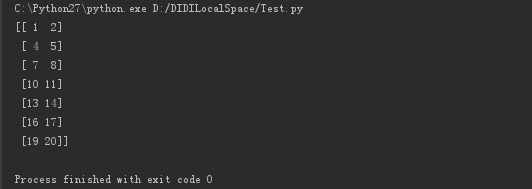
第三个：

 np.concatenate((class1_sample, class2_sample), axis=1)

其中主要对axis=0和axis=1的问题做一下笔记：

axis=0时：数组的拼接方式为首尾相连接

a = np.array([[1, 2], [3, 4]])

b = np.array([[5, 6]])

c = np.concatenate((a, b), axis=0)
输出为：
array([[1, 2],
[3, 4],
[5, 6]])

axis=1时：数组的拼接方式为在a的每行元素末尾添加b对应行元素。

a = np.array([[1, 2], [3, 4]])

b = np.array([[5, 6]])

c = np.concatenate((a, b), axis=1)
输出为：
array([[1, 2,3],
[4，5, 6]])