C语言 | 计算器实现（中缀表示法/后缀表示法）

————————————————————————————————————————————

实现原理：

每个操作数都被依次压入栈中，当一个运算符到达时，从栈中弹出相应数目的操作数（对于二元运算符来说是两个操作数），把该运算符作用于弹出的操作数，并把运算结果再压入栈中

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

计算器（后缀表达式）

相关知识：

后缀表达式（逆波兰表示法）：在逆波兰中，所有运算符都跟在操作数后面，如下：(1 - 2) *(4 + 5) 采用逆波兰表示法表示为：1 2 - 4 5 + *，不需要圆括号，只要知道每个运算符需要几个操作数就不会引起歧义

实现功能：

输入后缀表达式，以换行结束，计算四则运算结果。

对于 1 2 - 4 5 + * 来说，首先把1和2压入到栈中，再用两者之差-1取代它们；然后将4和5压入到栈中，再用两者之和9取代它们。最后从栈中取出栈顶的-1和9，并把它们的积-9压入到栈顶。到达输入行的末尾时，把栈顶的值弹出来并打印。

伪代码：

while 读入值不为换行时

if 是数字

压入栈中

else if 是运算符

弹出两个运算数，计算并压栈

else 输入错误并退出

end if

读入值

弹出最终结果并打印

实现代码：

 /* 实现功能：输入后缀表达式，以换行结束，计算四则运算结果 */
 /* 这种后缀表示法只需要一个栈就可以了,遇到符号则弹运算数,但是中缀就不一样 */
 #include <stdio.h>
 #include <stdlib.h>
 #define OK 1
 #define ERROR 0
 #define OVERFLOW -2
 #define STACK_INIT_SIZE 100
 #define STACKINCREAMENT 10
 typedef int Status;
 typedef char SElemType;
 typedef struct
 {
     SElemType *top;
     SElemType *base;
     int stacksize;
 } SqStack;
 Status InitStack(SqStack *s)
 {
     s->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
     if (!s->base) exit(OVERFLOW);
     s->top = s->base;
     s->stacksize = STACK_INIT_SIZE;
     return OK;
 }
 Status Push(SqStack *s, SElemType e)
 {
     if (s->top - s->base == s->stacksize)
     {
         s->base = (SElemType *)realloc(s->base, (s->stacksize + STACKINCREAMENT) * sizeof(SElemType));
         if (!s->base) exit(OVERFLOW);
         s->top = s->base + s->stacksize;
         s->stacksize += STACKINCREAMENT;
     }
     s->top++;
     *(s->top) = e;
     return OK;
 }
 Status Pop(SqStack *s, SElemType *e)
 {
     if (s->top == s->base) exit(OVERFLOW);
     *e = *(s->top);
     s->top--;
     return OK;
 }
 Status Empty(SqStack s)
 {
     if (s.top - s.base == )
         return OK;
     else
         return ERROR;
 }
 int main()
 {
     SqStack OPND; //OPTR是运算符 OPND是运算数
     char c, num1, num2;
     InitStack(&OPND);
     while((c = getchar()) != '\n')
     {
         switch(c)
         {
         case '':
         case '':
         case '':
         case '':
         case '':
         case '':
         case '':
         case '':
         case '':
         case '':
             Push(&OPND, c - '');
             break;
         case '+':
             Pop(&OPND, &num2);
             Pop(&OPND, &num1);
             Push(&OPND, num1 + num2);
             break;
         case '-':
             Pop(&OPND, &num2);
             Pop(&OPND, &num1);
             Push(&OPND, num1 - num2);
             break;
         case '*':
             Pop(&OPND, &num2);
             Pop(&OPND, &num1);
             Push(&OPND, num1 * num2);
             break;
         case '/':
             Pop(&OPND, &num2);
             Pop(&OPND, &num1);
             Push(&OPND, num1 / num2);
             break;
         default:
             break;
         }
     }
     while(!Empty(OPND))
     {
         Pop(&OPND, &c);
         printf("%d ", c);
     }
     return OK;
 }

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

计算器（中缀表示法）

运算符优先级：

	+	-	*	/	(	)	#
+	>	>	<	<	<	>	>
-	>	>	<	<	<	>	>
*	>	>	>	>	<	>	>
/	>	>	>	>	<	>	>
(	<	<	<	<	<	=	0
)	>	>	>	>	0	>	>
#	<	<	<	<	<	0	=

执行过程：

在计算 #4+3*(5-10)/5# 时栈中的执行过程如下

步骤	输入字符	执行操作	OPTR	OPND
1	#	Push(#)	#
2	4	Push(4)	#	4
3	+	'#'<'+',Push(+)	# +	4
4	3	Push(3)	# +	4 3
5	*	'+'<'*',Push(*)	# + *	4 3
6	(	'*'<'(',Push(()	# + * (	4 3
7	5	Push(5)	# + * (	4 3 5
8	-	'('<'-',Push(-)	# + * ( -	4 3 5
9	10	Push(10)	# + * ( -	4 3 5 10
10	)	'-'>')',计算并压入结果	# + * (	4 3 -5
11		'('=')',脱括号	# + *	4 3 -5
12	/	'*'>'/'计算并压入结果	# +	4 -15
13		'+'<'/',Push(/)	# + /	4 -15
14	5	Push(5)	# + /	4 -15 5
15	#	'/'>'#',计算并压入结果	# +	4 -3
16		'+'>'#',计算并压入结果	#	1
17		'#'='#',脱括号		1

伪代码：

初始化运算符栈；压入#；

初始化运算数栈；获取输入；

while 获取输入不为#或栈顶不为#

if 输入的是数字

压入运算数栈

获取输入

if 新输入的也是数字

十位数百位数运算

end if

else

switch 运算符栈顶与当前输入优先级比较

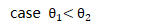
压入运算符栈

获得输入

弹出运算符栈顶（或#

获得输入

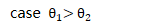
弹出运算符栈顶

弹出两个运算数

计算并将结果压入运算数栈

//此时不获取新输入，该循环输入的运算符作为c重新进入循环

end if

end while

输出运算数栈中剩的运算数

实现代码：

 /* 只能运算-128~127之间的结果 */
 #include <stdio.h>
 #include <stdlib.h>
 #include <math.h>
 #define OK 1
 #define ERROR 0
 #define SPILL -2 //math.h中已有OVERFLOW,则改用SPILL
 #define STACK_INIT_SIZE 100
 #define STACKINCREAMENT 10
 typedef char SElemType;
 typedef int Status;
 typedef struct
 {
     SElemType *top;
     SElemType *base;
     int stacksize;
 } SqStack;
 Status InitStack(SqStack *s)
 {
     s->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
     if (!s->base)
         exit(SPILL);
     s->top = s->base;
     s->stacksize = STACK_INIT_SIZE;
     return OK;
 }
 Status EmptyStack(SqStack s)
 {
     if (s.top - s.base == )
         return OK;
     else
         return ERROR;
 }
 Status Push(SqStack *s, SElemType e)
 {
     if (s->top - s->base == s->stacksize)
     {
         s->base = (SElemType *)realloc(s->base, (s->stacksize + STACKINCREAMENT) * sizeof(SElemType));
         if (!s->base)
             exit(SPILL);
         s->top = s->base + s->stacksize;
         s->stacksize += STACKINCREAMENT;
     }
     s->top ++;
     *(s->top) = e;
     return OK;
 }
 Status Pop(SqStack *s, SElemType *e)
 {
     if (s->top == s->base)
         exit(SPILL);
     *e = *(s->top);
     s->top--;
     return OK;
 }
 SElemType GetTop(SqStack s)
 {
     return *(s.top);
     // *e = *(s.top);
     // return OK;
 }
 /* 判断如果是数字则返回OK,运算符返回ERROR,非法输入则退出 */
 Status InputJudge(SElemType c)
 {
     switch(c)
     {
     case '':
     case '':
     case '':
     case '':
     case '':
     case '':
     case '':
     case '':
     case '':
     case '':
         return OK;
         break;
     case '+':
     case '-':
     case '*':
     case '/':
     case '(':
     case ')':
     case '#':
         return ERROR;
         break;
     default:
         exit(SPILL);
         break;
     }
 }
 /* 当前输入的运算符和前一个运算符比较优先级 */
 SElemType PriorityJudge(SElemType optr1, SElemType optr2)
 {
     int i, j;
     char priorityTable[][] =
     {
         {'>', '>', '<', '<', '<', '>', '>'},
         {'>', '>', '<', '<', '<', '>', '>'},
         {'>', '>', '>', '>', '<', '>', '>'},
         {'>', '>', '>', '>', '<', '>', '>'},
         {'<', '<', '<', '<', '<', '=', ''},
         {'>', '>', '>', '>', '', '>', '>'},
         {'<', '<', '<', '<', '<', '', '='}
     };
     switch(optr1)
     {
     case '+':
         i = ;
         break;
     case '-':
         i = ;
         break;
     case '*':
         i = ;
         break;
     case '/':
         i = ;
         break;
     case '(':
         i = ;
         break;
     case ')':
         i = ;
         break;
     case '#':
         i = ;
         break;
     }
     switch(optr2)
     {
     case '+':
         j = ;
         break;
     case '-':
         j = ;
         break;
     case '*':
         j = ;
         break;
     case '/':
         j = ;
         break;
     case '(':
         j = ;
         break;
     case ')':
         j = ;
         break;
     case '#':
         j = ;
         break;
     }
     return priorityTable[i][j];
 }
 /* 四则运算 */
 SElemType Calc(SElemType optr, SElemType num1, SElemType num2)
 {
     switch(optr)
     {
     case '+':
         return (num1 + num2);
         break;
     case '-':
         return (num1 - num2);
         break;
     case '*':
         return (num1 * num2);
         break;
     case '/':
         return (num1 / num2);
         break;
     }
 }
 int main()
 {
     char c, optr, num1, num2, temp;
     SqStack OPND, OPTR;
     InitStack(&OPTR);
     Push(&OPTR, '#');
     InitStack(&OPND);
     c = getchar();
     while(c != '#' || GetTop(OPTR) != '#')
     // while(!EmptyStack(OPTR))
     //严蔚敏老师书上的算法是判断输入非#或栈顶非#时循环,个人认为判断运算符栈不为空也可以,当初始化时压入的#闭合,结束运算
     {
         if (InputJudge(c))
         {
             Push(&OPND, c - '');
             c = getchar();
             /* 当连续输入数字时,计算十位数和百位数 */
             while(InputJudge(c))
             {
                 int i = ;
                 Pop(&OPND, &temp);
                 Push(&OPND, temp * pow(, i) + (c - ''));
                 i++;
                 c = getchar();
             }
         }
         else
             switch(PriorityJudge(GetTop(OPTR), c))
             {
             case '<':
                 Push(&OPTR, c);
                 c = getchar();
                 break;
             case '=':
                 Pop(&OPTR, &c);
                 c = getchar();
                 break;
             case '>':
                 Pop(&OPTR, &optr);
                 Pop(&OPND, &num2);
                 Pop(&OPND, &num1);
                 Push(&OPND, Calc(optr, num1, num2));
                 break;
             }
     }
     while(!EmptyStack(OPND))
     {
         Pop(&OPND, &c);
         printf("%d\n", c);
     }
     return OK;
 }