Gradient Boosting算法简介

最近项目中涉及基于Gradient Boosting Regression 算法拟合时间序列曲线的内容，利用python机器学习包 scikit-learn 中的GradientBoostingRegressor完成

因此就学习了下Gradient Boosting算法，在这里分享下我的理解

Boosting 算法简介

Boosting算法，我理解的就是两个思想：

1）“三个臭皮匠顶个诸葛亮”，一堆弱分类器的组合就可以成为一个强分类器；

2）“知错能改，善莫大焉”，不断地在错误中学习，迭代来降低犯错概率

当然，要理解好Boosting的思想，首先还是从弱学习算法和强学习算法来引入：

1）强学习算法：存在一个多项式时间的学习算法以识别一组概念，且识别的正确率很高；

2）弱学习算法：识别一组概念的正确率仅比随机猜测略好；

Kearns & Valiant证明了弱学习算法与强学习算法的等价问题，如果两者等价，只需找到一个比随机猜测略好的学习算法，就可以将其提升为强学习算法。

那么是怎么实现“知错就改”的呢？

Boosting算法，通过一系列的迭代来优化分类结果，每迭代一次引入一个弱分类器，来克服现在已经存在的弱分类器组合的shortcomings

　　在Adaboost算法中，这个shortcomings的表征就是权值高的样本点

　　而在Gradient Boosting算法中,这个shortcomings的表征就是梯度

无论是Adaboost还是Gradient Boosting，都是通过这个shortcomings来告诉学习器怎么去提升模型，也就是“Boosting”这个名字的由来吧

Adaboost算法

Adaboost是由Freund 和 Schapire在1997年提出的，在整个训练集上维护一个分布权值向量W,用赋予权重的训练集通过弱分类算法产生分类假设（基学习器）y(x),然后计算错误率,用得到的错误率去更新分布权值向量w,对错误分类的样本分配更大的权值,正确分类的样本赋予更小的权值。每次更新后用相同的弱分类算法产生新的分类假设,这些分类假设的序列构成多分类器。对这些多分类器用加权的方法进行联合,最后得到决策结果。

其结构如下图所示：

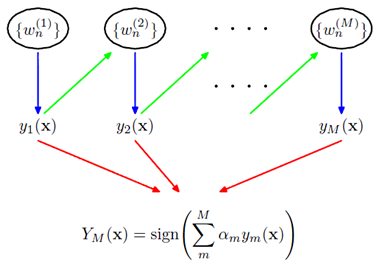
前一个学习器改变权重w，然后再经过下一个学习器，最终所有的学习器共同组成最后的学习器。

如果一个样本在前一个学习器中被误分，那么它所对应的权重会被加重，相应地，被正确分类的样本的权重会降低。

这里主要涉及到两个权重的计算问题：

1）样本的权值

　　1> 没有先验知识的情况下,初始的分布应为等概分布,样本数目为n,权值为1/n

　　2> 每一次的迭代更新权值，提高分错样本的权重

2）弱学习器的权值

　　1> 最后的强学习器是通过多个基学习器通过权值组合得到的。

　　2> 通过权值体现不同基学习器的影响,正确率高的基学习器权重高。实际上是分类误差的一个函数

Gradient Boosting

和Adaboost不同，Gradient Boosting 在迭代的时候选择梯度下降的方向来保证最后的结果最好。

损失函数用来描述模型的“靠谱”程度，假设模型没有过拟合，损失函数越大，模型的错误率越高

如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度方向上下降。

下面这个流程图是Gradient Boosting的经典图了，数学推导并不复杂，只要理解了Boosting的思想，不难看懂

这里是直接对模型的函数进行更新，利用了参数可加性推广到函数空间。

训练F0-Fm一共m个基学习器，沿着梯度下降的方向不断更新ρ_m和a_m

GradientBoostingRegressor实现

python中的scikit-learn包提供了很方便的GradientBoostingRegressor和GBDT的函数接口，可以很方便的调用函数就可以完成模型的训练和预测

GradientBoostingRegressor函数的参数如下：

class sklearn.ensemble.GradientBoostingRegressor(loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort='auto')[source]¶

loss: 选择损失函数，默认值为ls(least squres)

learning_rate: 学习率，模型是0.1

n_estimators: 弱学习器的数目，默认值100

max_depth: 每一个学习器的最大深度，限制回归树的节点数目，默认为3

min_samples_split: 可以划分为内部节点的最小样本数，默认为2

min_samples_leaf: 叶节点所需的最小样本数，默认为1

……

可以参考   http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html

官方文档里带了一个很好的例子，以500个弱学习器，最小平方误差的梯度提升模型，做波士顿房价预测，代码和结果如下：

 import numpy as np
 import matplotlib.pyplot as plt

 from sklearn import ensemble
 from sklearn import datasets
 from sklearn.utils import shuffle
 from sklearn.metrics import mean_squared_error

 ###############################################################################
 # Load data
 boston = datasets.load_boston()
 X, y = shuffle(boston.data, boston.target, random_state=13)
 X = X.astype(np.float32)
 offset = int(X.shape[0] * 0.9)
 X_train, y_train = X[:offset], y[:offset]
 X_test, y_test = X[offset:], y[offset:]

 ###############################################################################
 # Fit regression model
 params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1,
           'learning_rate': 0.01, 'loss': 'ls'}
 clf = ensemble.GradientBoostingRegressor(**params)

 clf.fit(X_train, y_train)
 mse = mean_squared_error(y_test, clf.predict(X_test))
 print("MSE: %.4f" % mse)

 ###############################################################################
 # Plot training deviance

 # compute test set deviance
 test_score = np.zeros((params['n_estimators'],), dtype=np.float64)

 for i, y_pred in enumerate(clf.staged_predict(X_test)):
     test_score[i] = clf.loss_(y_test, y_pred)

 plt.figure(figsize=(12, 6))
 plt.subplot(1, 2, 1)
 plt.title('Deviance')
 plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-',
          label='Training Set Deviance')
 plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
          label='Test Set Deviance')
 plt.legend(loc='upper right')
 plt.xlabel('Boosting Iterations')
 plt.ylabel('Deviance')

 ###############################################################################
 # Plot feature importance
 feature_importance = clf.feature_importances_
 # make importances relative to max importance
 feature_importance = 100.0 * (feature_importance / feature_importance.max())
 sorted_idx = np.argsort(feature_importance)
 pos = np.arange(sorted_idx.shape[0]) + .5
 plt.subplot(1, 2, 2)
 plt.barh(pos, feature_importance[sorted_idx], align='center')
 plt.yticks(pos, boston.feature_names[sorted_idx])
 plt.xlabel('Relative Importance')
 plt.title('Variable Importance')
 plt.show()

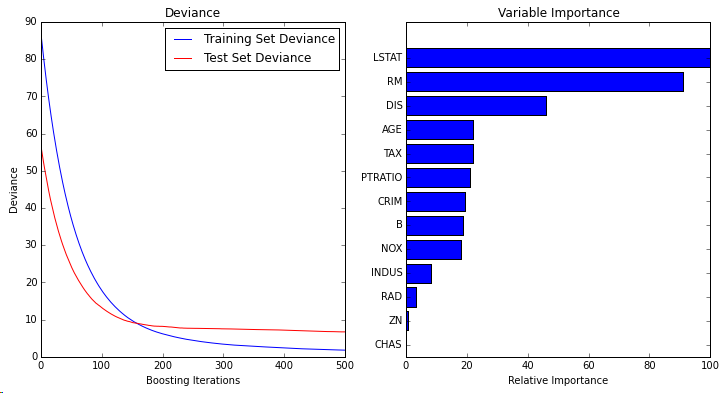
可以发现，如果要用Gradient Boosting 算法的话，在sklearn包里调用还是非常方便的，几行代码即可完成，大部分的工作应该是在特征提取上。

感觉目前做数据挖掘的工作，特征设计是最重要的，据说现在kaggle竞赛基本是GBDT的天下，优劣其实还是特征上，感觉做项目也是，不断的在研究数据中培养对数据的敏感度。

数据挖掘刚刚起步，希望是个好的开头，待续……