MATLAB线性回归方程与非线性回归方程的相关计算

每次比赛都需要查一下，这次直接总结到自己的博客中。

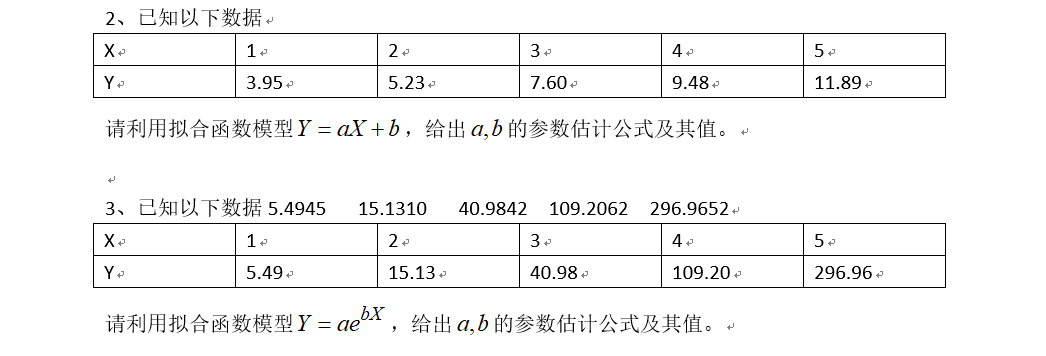
以这个为例子：

2.线性方程的相关计算

x=[1,2,3,4,5]';%参数矩阵
X=[ones(5,1),x];%产生一个5行一列的矩阵，后接x矩阵
Y=[3.95,5.23,7.6,9.48,11.89]';
[b,bint,r,rint,stats]=regress(Y,X)
%b为方程相关系数
%r表示残差
%rint表示置信区间
%stats适用于检验回归模型的统计量

　

得到

b =

    1.5910
    2.0130

bint =

    0.4482    2.7338
    1.6684    2.3576

r =

    0.3460
   -0.3870
   -0.0300
   -0.1630
    0.2340

rint =

   -0.0946    0.7866
   -1.3318    0.5578
   -1.6413    1.5813
   -1.5888    1.2628
   -0.6578    1.1258

stats =

    0.9914  345.6401    0.0003    0.1172

　

stats计算的结果，分别表示复相关系数r^2=0.9914,检验回归方差显著性的统计量F=345.6401，对应所得F统计量的概率P=0.003，估计误差方差=0.1172。

r^2越接近1，回归效果越显著；p<0.05表明方程成立。

rcoplot(r,rint)%残差图制作，红色表示异常点（不经过x=0)

　　

预测及作图

z=b(1)+b(2)*x
plot(x,Y,'k+',x,z,'r')

　　

z =

    3.6040
    5.6170
    7.6300
    9.6430
   11.6560

　　

　　

3.非线性方程的相关计算

x=[1,2,3,4,5]';%参数矩阵，并转置
y=[5.49,15.13,40.98,109.20,296.96]';
beta0=[1.9635 1.02097]';%待定参数的初始值
[beta,r,J]=nlinfit(x,y,@modelfun,beta0);%非线性方程回归命令
beta,r,J

　　

创建modelfunc.m函数

function yhat=modelfun(beta,x)
%UNTITLED Summary of this function goes here
%   Detailed explanation goes here
yhat=beta(1)*exp(beta(2)*x);
end

　　

当然对于函数的建立也可以直接在主代码中使用函数

x=[1,2,3,4,5]';%参数矩阵
y=[5.49,15.13,40.98,109.20,296.96]';
beta0=[1.9635 1.02097]';%待定参数的初始值
modelfu=inline('beta(1)*exp(beta(2)*x)','beta','x');
[beta,r,J]=nlinfit(x,y,modelfu,beta0);%非线性方程回归命令
beta,r,J

　　

beta =

    2.0389
    0.9962

r =

   -0.0311
    0.1792
    0.4944
   -0.4322
    0.0837

J =

   1.0e+03 *

    0.0027    0.0055
    0.0073    0.0299
    0.0199    0.1215
    0.0538    0.4385
    0.1456    1.4844

　　

beta为估计出的回归系数    r表示残差    J表示Jacobian矩阵     modelfun:匿名函数（内联函数）  beta0表示回归系数的初值

待定参数的初始值

beta0的计算需要代入两组x,y的值进行计算，这样有助于MATLAB快速确定计算范围

预测和预测误差估计

[Y,DELTA]=nlpredci('modelfun', x,beta,r,J)

　　

Y =

    5.5211
   14.9508
   40.4856
  109.6322
  296.8763

DELTA =

    0.1977
    0.3981
    0.7093
    0.9588
    1.2499

　　

获取 x 处的预测值 Y 及预测值的显著性为 1-alpha 的置信区间 Y±DELTA

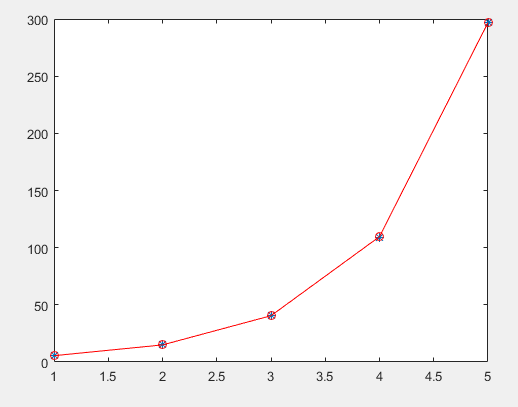
作图

plot(x,y,'*',x,Y,'-or')