bzoj4772 显而易见的数论

题意：http://www.lydsy.com/JudgeOnline/problem.php?id=4772

sol ：这个题卡了我一整天QAQ

　　　出题人简直丧心病狂，卡内存+卡常数QAQ

　　　题意就是，给你一个整数，让你求所有整数划分的方案数的价值和，价值是个函数

　　　长成这个样子：

　　　∑_{划分方案数}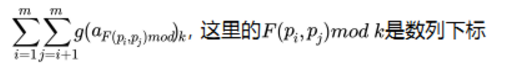

　　　然后就是，考虑枚举pi和pj，如何算这个二元组在整数划分中出现的次数

　　　记sum[i]为将i进行整数划分的方案数（实际操作时为避免数组下标为负所以将sum反向）

sum[]=;
for(int i=;i<=n;i++)
{
    for(int j=;j<=n;j++)
    {
        if(i==||j==) f[i][j]=;
        else if(i==j) f[i][j]=(f[i][j-]+)%p;
        else if(i<j) f[i][j]=f[i][j-];
        else f[i][j]=(f[i-j][j]+f[i][j-])%p;
    }
    sum[i]=f[i][i];
}

　　　当pi!=pj的时候，枚举pi和pj出现的次数muli,mulj，那么答案即为ans[pi][pj]+=sum[n-pi*muli-pj*mulj]

　　　而当pi=pj时，同样枚举pi出现的次数，我们要考虑两两组合的方案数

　　　　　即ans[pi][pi]+=muli*(muli-1)/2*(sum[muli*pi]-sum[(muli+1)*pi])

　　　然后我到这就不会了QAQ，于是去请教了Nbc和Claris，%%%

　　　Nbc表示这个题就是个暴力随便搞搞就行了......我：

　　　Claris表示其实这个g是个积性函数......我：

　　　好了这个题可以做了QAQ

　　　我们考虑g(n)在n为质数的情况下的值为2n-2，所以直接预处理线性筛一发g(x)就行了QAQ

　　　然后对于那个F(i,j)我们可以预处理一发gcd和pow就可以O(1)做了

　　　于是我们的做法就是，枚举不相等的i和j，统计答案

for(int i=;i<=n;i++)
    for(int j=i+;j<=n-i;j++)
        for(int muli=;muli*i+j<=n;muli++)
            for(int mulj=;mulj*j+muli*i<=n;mulj++)
                ans+=g[a[F(i,j)]]*sum[muli*i+mulj*j]%p,ans%=p;

　　　然后再枚举相等的i和j，统计答案

for(int i=;i<=n;i++)
    for(int muli=;muli*i<=n;muli++)
        ans=(ans+g[a[F(i,i)]]*muli*(muli-)/*(sum[muli*i]-sum[(muli+)*i]+p))%p;

　　　然后我们就愉悦的发现他0ms TLE了

　　　哦....原来是define int long long炸内存了啊QAQ

　　　简单的改了改然后交上去，发现他又偷♂税的T掉了......

　　　我们发现在统计不相等的i和j时的取模操作太多了QAQ

　　　于是我们可以手动实现一发取模操作...然而我并不会乘法取模，怎么办呢？

　　　我们发现乘法取模是因为乘了一个g[]，然而F(i,j)的范围只有1e5，奥妙重重

　　　考虑开一个数组Cnt记录F的每个值的访问次数，这样的话在后面一次性统计即可

for(int i=;i<=n;i++)
　　for(int j=i+;j<=n-i;j++)
　　　　for(int muli=;muli*i+j<=n;muli++)
　　　　　　for(int mulj=;mulj*j+muli*i<=n;mulj++)
　　　　　　　　mod(Cnt[F(i,j)],sum[muli*i+mulj*j]);
for(int i=;i<K;i++) ans+=1LL*g[a[i]]*Cnt[i]%p,ans%=p;

　　　于是这道题就可以切掉了QwQ

　　　附上完整代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int p=1e9+;
const int Mx1=;
const int Mx2=1e7+;
int tp,n,K,a[Mx2],sum[Mx1],f[Mx1][Mx1],gcd[Mx1][Mx1],mul[Mx1][Mx1];
int cnt,ans,pri[Mx2],tmp[Mx2],g[Mx2],b[Mx1];
bool jud[Mx2];
inline void pre()
{
    sum[n]=;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            if(i==||j==) f[i][j]=;
            else if(i==j) f[i][j]=(f[i][j-]+)%p;
            else if(i<j) f[i][j]=f[i][j-];
            else f[i][j]=(f[i-j][j]+f[i][j-])%p;
        }
        sum[n-i]=f[i][i];
    }
    g[]=,g[]=;
    for(int i=;i<=1e7;i++)
    {
        if(!jud[i]) pri[++cnt]=tmp[i]=i,g[i]=(*i-)%p;
        for(int j=;j<=cnt&&i*pri[j]<=1e7;j++)
        {
            jud[i*pri[j]]=;
            if(i%pri[j])
                tmp[i*pri[j]]=pri[j],
                g[i*pri[j]]=g[i]*g[pri[j]]%p;
            else
            {
                tmp[i*pri[j]]=tmp[i]*pri[j];
                if(tmp[i]!=i) g[i*pri[j]]=1LL*g[i/tmp[i]]*g[tmp[i]*pri[j]]%p;
                else g[i*pri[j]]=(1LL*g[i]*pri[j]+i*pri[j]-i)%p;
                break;
            }
        }
    }
    for(int i=;i<=n;i++) gcd[i][]=gcd[][i]=gcd[i][i]=i,gcd[][i]=gcd[i][]=;
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
        {
            if(!gcd[i][j]) gcd[i][j]=gcd[j][i-j];
            gcd[j][i]=gcd[i][j];
        }
    for(int i=;i<=n;i++)
    {
        mul[i][]=;
        for(int j=;j<=n;j++) mul[i][j]=(1LL*mul[i][j-]*i)%K;
    }
}
 
inline int F(int pi,int pj)
{
    if(tp==) return %K;
    if(tp==) return (gcd[pi][pj])%K;
    if(tp==) return (mul[pi][pj]+mul[pj][pi]+(pi^pj))%K;
}
 
inline void mod(int &x,const int &y){
    x+=y;
    if (x>=p) x-=p;
}
 
int Cnt[Mx2];
int main()
{
    scanf("%d%d%d",&tp,&n,&K);
    for(int i=;i<K;i++) scanf("%d",&a[i]);
    pre();
    for(int i=;i<=n;i++)
        for(int j=i+;j<=n-i;j++)
            for(int muli=;muli*i+j<=n;muli++)
                for(int mulj=;mulj*j+muli*i<=n;mulj++)
                    mod(Cnt[F(i,j)],sum[muli*i+mulj*j]);
    for(int i=;i<K;i++) ans+=1LL*g[a[i]]*Cnt[i]%p,ans%=p;
    for(int i=;i<=n;i++)
    {
        for(int muli=;muli*i<=n;muli++)
        {
            int Tmp=1LL*muli*(muli-)/*(sum[muli*i]-sum[(muli+)*i]+p)%p;
              mod(ans,1LL*g[a[F(i,i)]]*Tmp%p);
        }
    }
    cout<<ans<<endl;
    return ;
}