Uva 11997 多路归并

题目链接：https://uva.onlinejudge.org/external/119/11997.pdf

题意：

k*k的矩阵，从每一行中选一个元素加起来，可以得到 k^k个和，求前 k 个最小值。

分析：

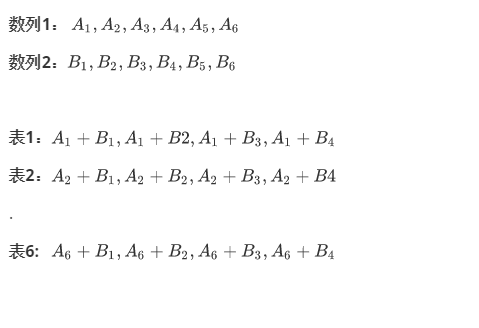
先把表头都放到优先队列中，每出一个，就从相应的表后面加一个。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = ;

 int A[maxn][maxn];

 struct Item {
     int s,b;
     bool operator < (const Item& rhs) const {
         return s > rhs.s;
     }
 };

 void merga(int* A,int* B,int* C,int n) {
     priority_queue<Item> Q;
     for(int i=;i<n;i++) {
         Q.push((Item){A[i]+B[],});
     }

     for(int i=;i<n;i++) {
         Item item = Q.top();Q.pop();
         C[i] = item.s;
         int b = item.b;
         if(b+<n) Q.push((Item){item.s-B[b]+B[b+],b+});
     }
 }

 int main(int argc, char** argv) {
     int n;
     while(scanf("%d",&n)!=EOF) {
         for(int i=;i<n;i++) {
             for(int j=;j<n;j++) {
                 scanf("%d",&A[i][j]);
             }
             sort(A[i],A[i]+n);
         }

         for(int i=;i<n;i++) {
             merga(A[],A[i],A[],n);
         }

         printf("%d",A[][]);
         for(int i=;i<n;i++) {
             printf(" %d",A[][i]);
         }
         puts("");

     }
     return ;
 }