cf 215 C. Crosses yy题

链接：http://codeforces.com/problemset/problem/215/C

C. Crosses

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There is a board with a grid consisting of n rows and m columns,
the rows are numbered from 1 from top to bottom and the columns are numbered from 1 from
left to right. In this grid we will denote the cell that lies on row number i and column number j as (i, j).

A group of six numbers (a, b, c, d, x0, y0),
where 0 ≤ a, b, c, d, is a cross, and there
is a set of cells that are assigned to it. Cell (x, y)belongs to this set if at
least one of two conditions are fulfilled:

• |x0 - x| ≤ a and |y0 - y| ≤ b
• |x0 - x| ≤ c and |y0 - y| ≤ d

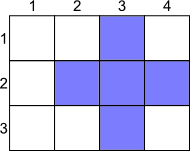The picture shows the
cross (0, 1, 1, 0, 2, 3) on the grid 3 × 4.

Your task is to find the number of different groups of six numbers, (a, b, c, d, x0, y0) that
determine the crosses of an area equal to s, which are placed entirely on the grid. The cross is placed entirely on the grid, if any
of its cells is in the range of the grid (that is for each cell (x, y) of the cross 1 ≤ x ≤ n; 1 ≤ y ≤ m holds).
The area of the cross is the number of cells it has.

Note that two crosses are considered distinct if the ordered groups of six numbers that denote them are distinct, even if these crosses coincide as sets of points.

Input

The input consists of a single line containing three integers n, m and s (1 ≤ n, m ≤ 500, 1 ≤ s ≤ n·m).
The integers are separated by a space.

Output

Print a single integer — the number of distinct groups of six integers that denote crosses with area s and that are fully placed on then × m grid.

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64dspecifier.

Sample test(s)

input

2 2 1

output

4

input

3 4 5

output

4

Note

In the first sample the sought groups of six numbers are: (0, 0, 0, 0, 1, 1), (0, 0, 0, 0, 1, 2), (0, 0, 0, 0, 2, 1), (0, 0, 0, 0, 2, 2).

In the second sample the sought groups of six numbers are: (0, 1, 1, 0, 2, 2), (0, 1, 1, 0, 2, 3), (1, 0, 0, 1, 2, 2), (1, 0, 0, 1, 2, 3).

题意：

给你n*m矩阵，问有多少个不同的    (a, b, c, d, x0, y0) 
  面积等于s。

• |x0 - x| ≤ a and |y0 - y| ≤ b
• |x0 - x| ≤ c and |y0 - y| ≤ d

满足这个条件 相当于两个一x0 。y0 为中心的。边长全为奇数的矩形并。

一个矩形长为2a+1，宽为2b+1   还有一个是(2*c+1) * (2*d+1)

做法：

枚举当中一个矩形的长和宽。

假设面积超过s显然不行。

假设等于s。那么还有一个肯定比它小或者相等。

ans+=(n-i/2*2)*(m-j/2*2)*   (((i/2+1)*(j/2+1)-1)*2+1);

(n-i/2*2)*(m-j/2*2) 这个算有多少位子 能够做为矩形 中心

(((i/2+1)*(j/2+1)-1)*2+1)  枚举那个小的边长

假设小于s的话。枚举还有一个矩阵的长度。长度小于i

然后计算宽度。

宽度假设小于m而且也是奇数

ans+=(n-i/2*2)*(m-wid/2*2)*2;    枚举中心点能够在的位置。由于两个矩形不同所以abcd能够对换 所以*2

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <malloc.h>
#include <ctype.h>
#include <math.h>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
#include <stack>
#include <queue>
#include <vector>
#include <deque>
#include <set>
#include <map>

int main()
{

	int n,m,s;

	scanf("%d%d%d",&n,&m,&s);
	__int64 ans=0;
	for(int i=1;i<=n;i+=2)//枚举比較长的长方形 长度
	{
		for(int j=1;j<=m;j+=2)
		{
				if(i*j>s)
					continue;
				else if(i*j==s)//一个包括还有一个
				{
					ans+=(n-i/2*2)*(m-j/2*2)*   (((i/2+1)*(j/2+1)-1)*2+1);
					// 位子*枚举边长
				}
				else
				{
					for(int len=1;len<i;len+=2)//长小的
					{
						if((s-i*j)%len==0)
						{
							int wid=(s-i*j)/(len)+j;
							//长的 j
							//宽的 wid
							if(wid<=m&&(wid&1))
							ans+=(n-i/2*2)*(m-wid/2*2)*2;
							//确定位置 由于不同 所以abcd能够换 *2
						}
					}
				}
		}
	}
	printf("%I64d\n",ans);

	 scanf("%d%d%d",&n,&m,&s);
	return 0;
}