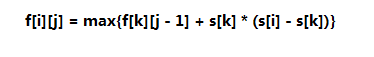[Bzoj3675][Apio2014]序列分割(斜率优化)
3675: [Apio2014]序列分割
Time Limit: 40 Sec Memory Limit: 128 MB
Submit: 4021 Solved: 1569
[Submit][Status][Discuss]
Description
Input
输入第一行包含两个整数n,k(k+1≤n)。
Output
输出第一行包含一个整数,为小H可以得到的最大分数。
Sample Input
Sample Output
HINT
【样例说明】
在样例中,小H可以通过如下3轮操作得到108分:
1.-开始小H有一个序列(4,1,3,4,0,2,3)。小H选择在第1个数之后的位置
将序列分成两部分,并得到4×(1+3+4+0+2+3)=52分。
2.这一轮开始时小H有两个序列:(4),(1,3,4,0,2,3)。小H选择在第3个数
字之后的位置将第二个序列分成两部分,并得到(1+3)×(4+0+2+
3)=36分。
3.这一轮开始时小H有三个序列:(4),(1,3),(4,0,2,3)。小H选择在第5个
数字之后的位置将第三个序列分成两部分,并得到(4+0)×(2+3)=
20分。
经过上述三轮操作,小H将会得到四个子序列:(4),(1,3),(4,0),(2,3)并总共得到52+36+20=108分。
【数据规模与评分】
:数据满足2≤n≤100000,1≤k≤min(n -1,200)。
分析:
斜率优化眼题,不想说啥,考试时10分钟切掉。
写的是apio原题,bzoj不需要输出方案,结果wa了一发
AC代码:
# include <iostream>
# include <cstdio>
using namespace std;
typedef long long LL;
const int N = 1e5 + ;
LL f[][N],s[N],ret;int n,k,cur,que[N],ans[N],pre[][N];
LL y(int i){return f[cur ^ ][i] - s[i] * s[i];}
LL x(int i){return s[i];}
LL Get(int A,int B){return f[cur ^ ][A] + s[A] * (s[B] - s[A]);}
LL Cross(int A,int B,int C){return (y(C) - y(B)) * (x(B) - x(A)) - (y(B) - y(A)) * (x(C) - x(B));}
int main()
{
scanf("%d %d",&n,&k);
for(int i = ;i <= n;i++)scanf("%lld",&s[i]);
for(int i = ;i <= n;i++)s[i] += s[i - ];
for(int j = ;j <= k;j++)
{
cur ^= ;int h = ,t = ;que[++t] = ;
for(int i = ;i <= n;i++)
{
while(h < t && Get(que[h],i) <= Get(que[h + ],i))h++;
f[cur][i] = Get(que[h],i);pre[j][i] = que[h];
while(h < t && Cross(que[t - ],que[t],i) >= )t--;
que[++t] = i;
}
}
printf("%lld\n",f[cur][n]);
int c = k,r = pre[c][n];
printf("%d",r);
while(pre[c - ][r])r = pre[--c][r],printf(" %d",r);
return ;
}
[Bzoj3675][Apio2014]序列分割(斜率优化)的更多相关文章
- bzoj3675[Apio2014]序列分割 斜率优化dp
3675: [Apio2014]序列分割 Time Limit: 40 Sec Memory Limit: 128 MBSubmit: 3508 Solved: 1402[Submit][Stat ...
- BZOJ3675: [Apio2014]序列分割(斜率优化)
Time Limit: 40 Sec Memory Limit: 128 MBSubmit: 4186 Solved: 1629[Submit][Status][Discuss] Descript ...
- [APIO2014]序列分割 --- 斜率优化DP
[APIO2014]序列分割 题目大意: 你正在玩一个关于长度为\(n\)的非负整数序列的游戏.这个游戏中你需要把序列分成\(k+1\)个非空的块.为了得到\(k+1\)块,你需要重复下面的操作\(k ...
- 【bzoj3675】[Apio2014]序列分割 斜率优化dp
原文地址:http://www.cnblogs.com/GXZlegend/p/6835179.html 题目描述 小H最近迷上了一个分隔序列的游戏.在这个游戏里,小H需要将一个长度为n的非负整数序列 ...
- P3648 [APIO2014]序列分割 斜率优化
题解:斜率优化\(DP\) 提交:\(2\)次(特意没开\(long\ long\),然后就死了) 题解: 好的先把自己的式子推了出来: 朴素: 定义\(f[i][j]\)表示前\(i\)个数进行\( ...
- BZOJ 3675 [Apio2014]序列分割 (斜率优化DP)
洛谷传送门 题目大意:让你把序列切割k次,每次切割你能获得 这一整块两侧数字和的乘积 的分数,求最大的分数并输出切割方案 神题= = 搞了半天也没有想到切割顺序竟然和答案无关...我太弱了 证明很简单 ...
- BZOJ3675 [Apio2014]序列分割 【斜率优化dp】
3675: [Apio2014]序列分割 Time Limit: 40 Sec Memory Limit: 128 MB Submit: 3366 Solved: 1355 [Submit][St ...
- BZOJ3675 [Apio2014]序列分割 动态规划 斜率优化
原文链接http://www.cnblogs.com/zhouzhendong/p/8697258.html 题目传送门 - BZOJ3675 题意 对于一个非负整数序列,小H需要重复k次以下的步骤: ...
- 【BZOJ3675】【APIO2014】序列分割 [斜率优化DP]
序列分割 Time Limit: 40 Sec Memory Limit: 128 MB[Submit][Status][Discuss] Description 小H最近迷上了一个分隔序列的游戏. ...
随机推荐
- Luogu P2397 yyy loves Maths VI (mode)
题目传送门 虽然只是一道黄题,但还是学到了一点新知识-- 摩尔投票法 用\(O(1)\)的内存,\(O(n)\)的时间来找出一串长度为n的数中的众数,前提是众数出现的次数要大于\(n/2\) 方法很简 ...
- Python学习笔记2(序列)
元组不可变序列 tuple函数 总结 字符串 基本字符串的操作 字符串格式化 字符串方法 find join lower replace split strip translate 小结 元组:不可变 ...
- Luogu P2123 皇后游戏(贪心)
题目链接:P2123 皇后游戏 如果证明这个题为什么是贪心的话,我是不会的,但是一看这个题目就是一个贪心,然后满足贪心的性质: 都能从两个人(东西)扩展到n个人(东西) 一定能从相邻状态扩展到不相邻的 ...
- verilog behaviral modeling -- procedural timing contronls
1.delay control : an expression specifies the time duration between initially encountering the state ...
- datetime模块,random模块
6.10自我总结 1.datetime模块(用于修改日期) import datetime print(datetime.datetime.now(),type(datetime.datetime.n ...
- 朋友去面试Python工程师,又带回来几道基础题,Python面试题No10
第1题: print 调用 Python 中底层的什么方法? print print() 用 sys.stdout.write() 实现 import sys print('hello') sys.s ...
- 水题:UVa253-Cube painting
Cube painting We have a machine for painting cubes. It is supplied with three different colors: blue ...
- Memcached特性及优缺点
为了加快文件访问速度且提供多个使用者.需要在内存中建立内存缓存数据的管理减小读写磁盘的次数及保证数据的更新.因为需要使用cache缓存. 1.Memcached 主要特性 a.数据仅存在于内存中, ...
- sublime_win配置
让你用sublime写出最完美的python代码--windows环境 点击上方标题查看原文链接, 感谢大佬 至少很长一段时间内,我个人用的一直是pycharm,也感觉挺好用的,也没啥大毛病 但是py ...
- Python基础之字符串,布尔值,整数,列表,元组,字典,集合
一.str字符串 1.capitalize字符串首字母大写 name = "json" v = name.capitalize() print(v) # 输出结果:Json 2.c ...