[Bzoj4182]Shopping（点分治）（树上背包）（单调队列优化多重背包）

4182: Shopping

---

Time Limit: 30 Sec  Memory Limit: 128 MB
Submit: 374  Solved: 130
[Submit][Status][Discuss]

Description

---

马上就是小苗的生日了，为了给小苗准备礼物，小葱兴冲冲地来到了商店街。商店街有n个商店，并且它们之间的道路构成了一颗树的形状。

第i个商店只卖第i种物品，小苗对于这种物品的喜爱度是wi，物品的价格为ci，物品的库存是di。但是商店街有一项奇怪的规定：如果在商店u,v买了东西，并且有一个商店w在u到v的路径上，那么必须要在商店w买东西。小葱身上有m元钱，他想要尽量让小苗开心，所以他希望最大化小苗对买

到物品的喜爱度之和。这种小问题对于小葱来说当然不在话下，但是他的身边没有电脑，于是他打电话给同为OI选手的你，你能帮帮他吗？

 

Input

---

输入第一行一个正整数T，表示测试数据组数。

对于每组数据，

第一行两个正整数n;m；

第二行n个非负整数w1,w2...wn；

第三行n个正整数c1,c2...cn；

第四行n个正整数d1,d2...dn；

接下来n-1行每行两个正整数u;v表示u和v之间有一条道路

 

Output

---

输出共T 行，每行一个整数，表示最大的喜爱度之和。

 

Sample Input

---

Sample Output

---

HINT

---

N<=500,M<=4000,T<=5,Wi<=4000,Di<=100

分析：

---

题意：两个点选了，它路径上的点必须选。求树上一个联通块的多重背包，权值最大。

题解：

 先用点分治假设重心必选，然后dfs它子树，这样每个点会做背包的次数降低到log次。

 

 然后dfs子树时列出dfs序，然后转移方程：

 

对于第二步，多重背包优化可以考虑二进制拆分总复杂度为O（Tnmlognlogm）。

也可以使用单调队列优化总复杂度O(Tnmlogn)

下面是对单调队列优化的图解：

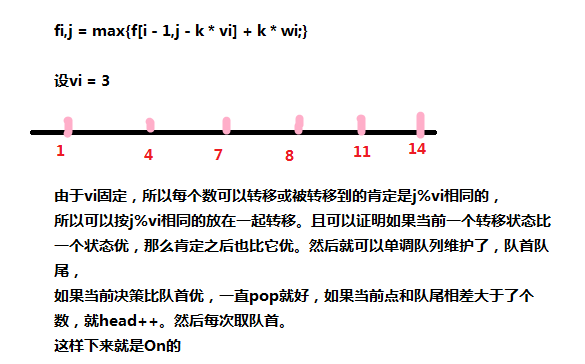
嗯。。没了。

AC代码：

---

# include <cstdio>
# include <cstring>
# include <iostream>
# include <algorithm>
using namespace std;
const int N = 4e3 + ;
const int M = 5e3 + ;
int mx[N],w[N],v[N],c[N],n,m,root,head[N],dt,sz[N],sum,id[N],ed[N],ans;
int f[N][M];
bool vis[N];
struct Edge{
    int to,nex;
}edge[N << ];
void AddEdge(int u,int v)
{
    edge[++dt] = (Edge){v,head[u]};
    head[u] = dt;
}
void find(int u,int pre)
{
    mx[u] = ;sz[u] = ;
    for(int i = head[u];i;i = edge[i].nex)
    {
        if(vis[edge[i].to] || edge[i].to == pre)continue;
        find(edge[i].to,u);
        sz[u] += sz[edge[i].to];
        mx[u] = max(mx[u],sz[edge[i].to]);
    }
    mx[u] = max(mx[u],sum - sz[u]);
    if(mx[u] < mx[root])root = u;
}
void dfs(int u,int pre)
{
    sz[u] = ;id[++dt] = u;
    for(int i = head[u];i;i = edge[i].nex)
    {
        if(vis[edge[i].to] || edge[i].to == pre)continue;
        dfs(edge[i].to,u);
        sz[u] += sz[edge[i].to];
    }
    ed[u] = dt;
}
int Q1[M],Q2[M];
void calc(int *g,int x)
{
    int h1,h2,t1,t2,cnt,t;
    for(int j = ;j < v[x];j++)
    {
        h1 = t1 = h2 = t2 = cnt = ;
        for(int k = j;k <= m;k += v[x])
        {
            if(t1 - h1 == c[x] + ){
                if(Q2[h2 + ] == Q1[h1 + ])++h2;
                ++h1;
            }
            t = g[k] - cnt * w[x];
            Q1[++t1] = t;
            while(h2 < t2 && Q2[t2] < t)--t2;
            Q2[++t2] = t;
            g[k] = Q2[h2 + ] + cnt * w[x];
            ++cnt;
        }
    }
}
void solve()
{
    for(int i = ;i <= dt + ;i++)
     for(int j = ;j <= m;j++)
     f[i][j] = ;
     int x,t;
    for(int i = dt;i >= ;i--)
    {
        x = id[i];
        for(int j = m;j >= v[x];j--)f[i][j] = f[i + ][j - v[x]] + w[x];
        calc(f[i],x);
        for(int j = m;j >= ;j--)f[i][j] = max(f[i][j],f[ed[x] + ][j]);
    }
    ans = max(ans,f[][m]);
}
void dfs(int u)
{
    vis[u] = true;dt = ;
    dfs(u,-);
    solve();
    for(int i = head[u];i;i = edge[i].nex)
    {
        if(vis[edge[i].to])continue;
        root = ;sum = sz[edge[i].to];
        if(sum > sz[u])sum = sum - sz[u];
        find(edge[i].to,u);
        dfs(root);
    }
}
int main()
{
    mx[] = N;
    int Case;scanf("%d",&Case);
    while(Case--)
    {
        scanf("%d %d",&n,&m);int x,y;
        memset(vis,false,sizeof vis);
        memset(head,,sizeof head);dt = ans = ;
        for(int i = ;i <= n;i++)scanf("%d",&w[i]);
        for(int i = ;i <= n;i++)scanf("%d",&v[i]);
        for(int i = ;i <= n;i++)scanf("%d",&c[i]),c[i]--;
        for(int i = ;i < n;i++)scanf("%d %d",&x,&y),AddEdge(x,y),AddEdge(y,x);
        root = ;sum = n;find(,-);
        dfs(root);
        printf("%d\n",ans);
    }
}