一个小误区 JS中的contains
在Java语言中,contains可以用于判断str1是否包含str2
原生JS中是有contains方法的
但它并不是字符串方法,,仅用于判断DOM元素的包含关系,参数是Element类型

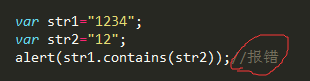
若要在JS中判断俩字符串的包含关系,用indexOf()
一个小误区 JS中的contains的更多相关文章
- 痞子衡嵌入式:关于i.MXRT中FlexSPI外设lookupTable里配置Normal read的一个小误区
大家好,我是痞子衡,是正经搞技术的痞子.今天痞子衡给大家介绍的是i.MXRT中FlexSPI外设lookupTable里配置Normal read的一个小误区. 关于串行四线NOR Flash,当其作 ...
- 关于SQL Server镜像的一个小误区
昨天晚上突然接到客户的电话, 说在配置了镜像的生产环境数据库下修改 “已提交读快照” 选项的时候报错, 需要先取消镜像然后再重新搭建.悲催的是这是个近TB的数据库,问我有没有什么快速的方法.于是我就问 ...
- 小程序 js中获取时间new date()的用法(网络复制过来自用)
js中获取时间new date()的用法 获取时间: 1 var myDate = new Date();//获取系统当前时间 获取特定格式的时间: 1 myDate.getYear(); //获 ...
- js实现小时钟,js中Date对象的使用?
介绍一下js中Date对象的使用 dateObj = new Date() dateObj = new Date(dateValue) dateObj = new Date(year,month,da ...
- SQL Server 中关于 @@error 的一个小误区
在SQL Server中,我常常会看到有些前辈这样写: ) ROLLBACK TRANSACTION T else COMMIT TRANSACTION T 一开始,我看见别人这么写,我就想当然的以为 ...
- 写一个小demo过程中遇到的各种问题 学生管理考勤系统(网页模拟)
添加与新增一些小玩意的1.0.3版本:传送门 各位带哥,这不是你们要的c++.java.c#作业哈 课上要求做个小作业,学生管理考勤系统,原本想着是个练手的好机会,结果只证实了我还是个弟中弟. 设想的 ...
- 一个经典的js中关于块级作用域和声明提升的问题
function functions(flag) { if (flag) { function getValue() { return 'a'; } } else { function getValu ...
- iframe与src一个性质 当js中修改了src的值后会重新向后台发送请求 ;为了防止浏览器缓存问题 当我们修改src时候 需要添加不同的值 这样浏览器就不会从缓存中取值 而是重新发起后台请求
- mysql 判断 字段为空 的一个小误区(又忘了)
今天判断mysql是否为空 直接写某字段 例 image_url !=null 结果数据库不报错误 并且没有返回相对数据. 又忘了这个事.今天特地记录一下. 因为null 表示什么也不是, 不能= ...
随机推荐
- 使用chcache 缓存
在项目里碰到了表单提交和ajax访问后台取到的request对象不是同一个对象,所以不能够资源共享,问了大神决定配置一个缓存来处理这个问题. 引用jar :ehcache-core-2.5.2.jar ...
- 洛谷 p1219 八皇后
刚参加完蓝桥杯 弱鸡错了好几道..回头一看确实不难 写起来还是挺慢的 于是开始了刷题的道路 蓝桥杯又名搜索杯 暴力杯...于是先从dfs刷起 八皇后是很经典的dfs问题 洛谷的这道题是这样的 上面的布 ...
- Windows Server 2012 添加角色时出现 failed to open runspace pool
先把所有的Windows Server 2012的更新更新了.再来添加服务器角色.就不会再出现 The Server Manager WinRM plug-in might be corrupted ...
- Python学习之路——Day02
今日内容: 1.编程语言介绍(***) 2.python介绍(***) 3.安装cpython解释器(多个版本)(****) 4.运行python程序的两种方式(****) 4.1 交互式 4.2 命 ...
- 当进行数据查询时候 要考虑创建一个model ;具备传入与输出的字段
当进行数据查询时候 要考虑创建一个model ;具备传入与输出的字段
- THEKEY
追溯历史,有据可查的身份证明是中国隋唐时期的“鱼符”,只为达官贵人证明身份等级,后演变为“龟符”.“牙牌”.“腰牌”等,直至近现代时期才出现真正意义的身份证,增加了个人信息描述.由于过去的生产力水平较 ...
- python初级装饰器编写
最近项目太忙好久没有学习python了,今天更新一下吧~~ 1.什么是python装饰器: 装饰器本质上是一个python函数,它可以让其他函数在不需要做任何代码变动的前提下增加额外的功能,装饰器的返 ...
- python学习日记(文件操作练习题)
登录注册(三次机会) name = input('请注册姓名:') password = input('请注册密码:') with open('log',mode='w',encoding='utf- ...
- Configure new Nagios clients
安装rpm -Uvh http://dl.fedoraproject.org/pub/epel/6/x86_64/epel-release-6-8.noarch.rpmrpm -Uvh http:// ...
- 【BZOJ1023】仙人掌图(仙人掌,动态规划)
[BZOJ1023]仙人掌图(仙人掌,动态规划) 题面 BZOJ 求仙人掌的直径(两点之间最短路径最大值) 题解 一开始看错题了,以为是求仙人掌中的最长路径... 后来发现看错题了一下就改过来了.. ...
