MT【251】椭圆中的好题

已知直线$l:x+y-\sqrt{3}=0$过椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,(a>b>0)$的右焦点且与椭圆$E$交于$A,B$两点,$P$为$AB$中点,$OP$的斜率为$\dfrac{1}{2}$.
(1)求椭圆$E$的方程;
(2)设$CD$是椭圆$E$的动弦,且其斜率为$1$,问椭圆$E$上是否存在定点$Q$,使得直线$QC,QD$的斜率分别为$k_1,k_2$满足$k_1+k_2=0?$若存在,求出$Q$的坐标;若不存在,请说明理由.

分析:(1)$c=\sqrt{3},k_{op}*k_l=-\dfrac{b^2}{a^2}$,易得$a^2=6,b^2=3$故$E:\dfrac{x^2}{6}+\dfrac{y^2}{3}=1$

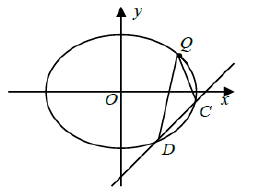
(2)特殊方法.设椭圆切线为$x-y+m=0$,切点为$M(x_0,y_0)$则$6+3-m^2=0$得$m^2=9$,又由椭圆的垂经定理得$k_{OM}*1=-\dfrac{3}{6}$故$\dfrac{y_0}{x_0}=-\dfrac{1}{2}$又$x_0-y_0+m=0$
解得$M(2,-1)\vee M(-2,1)$从而$Q(2,1)\vee Q(-2,-1)$

一般方法见最后附录：
相关内容:2014辽宁卷21题.
已知圆\(x^2+y^2=4\)的切线与\(x\)轴正半轴，\(y\)轴正半轴围成一个三角形．当该三角形的面积最小时切点为\(P\)．双曲线\(C_1:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)过点\(P\)且离心率为\(\sqrt 3\)
(1)求\(C_1\)的方程;
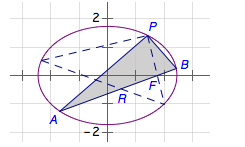
(2)椭圆\(C_2\)过点\(P\)且与\(C_1\)有相同的焦点，直线\(l\)过\(C_2\)的右焦点$F$且与\(C_2\)交于\(A\)，\(B\)两点．若以线段\(AB\)为直径的圆过点\(P\)，求\(l\)的方程．

解答:

(1)\(x^2-\dfrac {y^2}2=1\)
(2)不难得到\[C_2:\dfrac{x^2}6+\dfrac{y^2}3=1.\] \(P(\sqrt 2,\sqrt 2)\)，接下来，我们以\(P\)为原点，水平方向为\(x\)轴向重新建立平面直角坐标系，则新坐标系下的椭圆方程为 \[\dfrac{(x+\sqrt 2)^2}6+\dfrac{(y+\sqrt 2)^2}3=1.\] 整理得\[\dfrac 16x^2+\dfrac 13y^2+\dfrac{\sqrt 2}3x+\dfrac{2\sqrt 2}3y=0.\]
设直线\(mx+ny=1\)被椭圆截得的弦对\(P\)的张角为直角，则齐次化联立，有\[\dfrac 16x^2+\dfrac 13y^2+\left(\dfrac{\sqrt 2}3x+\dfrac{2\sqrt 2}3y\right)\cdot (mx+ny)=0.\] 从而有\[\dfrac 16+\dfrac 13+\dfrac{\sqrt 2}3m+\dfrac{2\sqrt 2}3n=0.\] 整理得\[-\dfrac{2\sqrt 2}3m-\dfrac{4\sqrt 2}3n=1.\] 因此该直线恒过点\(R\left(-\dfrac{2\sqrt 2}3,-\dfrac{4\sqrt 2}3\right)\).则原直线恒过$\left(\dfrac{\sqrt 2}3,-\dfrac{\sqrt 2}3\right)$ 
故直线$RF:y=\dfrac{3\sqrt{6}+2}{25}(x-\sqrt{3})$和直线$PF:y=-(2+\sqrt{6})(x-\sqrt{3})$
(注意：很容易遗漏直线$PF$, 事实上此时$A$ 点与$P$ 点重合)为所求．
注:1.椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$与直线$AX+BY+C=0$相切则$a^2A^2+b^2B^2-C^2=0$
2.涉及到椭圆上一个定点引出的两条弦的斜率$k_1,k_2$的和与乘积问题一般平移齐次化会出奇制胜.
3.涉及到椭圆里的弦的中点想到两个东西1.点差法 2.椭圆的垂经定理(可由点差法证明)
4.此题如果用仿射变换也可得到类似做法.
附一般做法: