[matlab] 6.粒子群优化算法

粒子群优化（PSO, particle swarm optimization）算法是计算智能领域，除了蚁群算法，鱼群算法之外的一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究。

实例分析1:

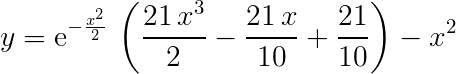
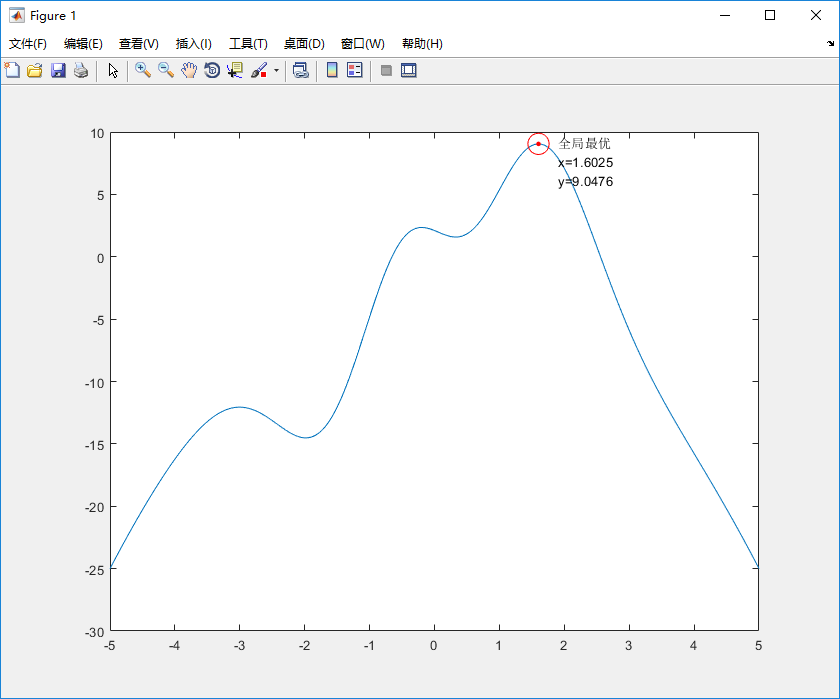
根据PSO算法思路求y最大值 ,其中x取值区间为[-5,5]

matlab代码如下：

%% I. 清空环境
clc
clear all

%% II. 绘制目标函数曲线图
x = -5:0.01:5;
y = 2.1*(1-x+5*x.^3).*exp(-x.^2/2)-x.^2;
figure
plot(x, y)
hold on

%% III. 参数初始化 这里默认惯性因子为1
c1 = 1.49445;   %加速常数 取Eberhart的参考值
c2 = 1.49445;   %加速常数 取Eberhart的参考值

maxgen = 30;   % 进化次数
sizepop = 100;   %种群规模

Vmax = 0.5;  %速度步长上限
Vmin = -0.5; %速度步长下限
popmax = 5; % x的上限
popmin = -5; % x的下限

%% IV. 产生初始粒子和速度
for i = 1:sizepop
    % 随机产生一个种群
    pop(i,:) = -10*rands(1)+5;    %产生[-5,5]的初始种群
    V(i,:) = 0.5 * rands(1);  %初始化[-0.5,0.5]速度
    % 利用fun.m子函数，计算适应度并存储到fitness(i)中
    fitness(i) = fun(pop(i,:));
end

%% V. 个体极值和群体极值
[bestfitness, bestindex] = max(fitness);
zbest = pop(bestindex,:);   %全局最佳
gbest = pop;    %个体最佳
fitnessgbest = fitness;   %个体最佳适应度值
fitnesszbest = bestfitness;   %全局最佳适应度值

%% VI. 迭代寻优
for i = 1:maxgen

    for j = 1:sizepop
        % 速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,V(j,:)>Vmax) = Vmax;
        V(j,V(j,:)<Vmin) = Vmin;

        % 种群更新
        pop(j,:) = pop(j,:) + V(j,:);
        pop(j,pop(j,:)>popmax) = popmax;
        pop(j,pop(j,:)<popmin) = popmin;

        % 适应度值更新
        fitness(j) = fun(pop(j,:));
    end

    for j = 1:sizepop
        % 个体最优更新
        if fitness(j) > fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end

        % 群体最优更新
        if fitness(j) > fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end
    yy(i) = fitnesszbest;
end

%% VII. 输出结果并绘图
[fitnesszbest zbest];
plot(zbest, fitnesszbest,'r.','MarkerSize',10)
plot(zbest, fitnesszbest,'ro','MarkerSize',16)
x_text=['x=',num2str(zbest)]; % x横坐标转换为字符串
y_text=['y=',num2str(fitnesszbest)];  % y横坐标转换为字符串
max_text=char('全局最优',x_text,y_text);  % 生成标志最大值点的字符串
text(zbest+0.3, fitnesszbest-1.4,max_text) %图上绘出全局最优的数据值
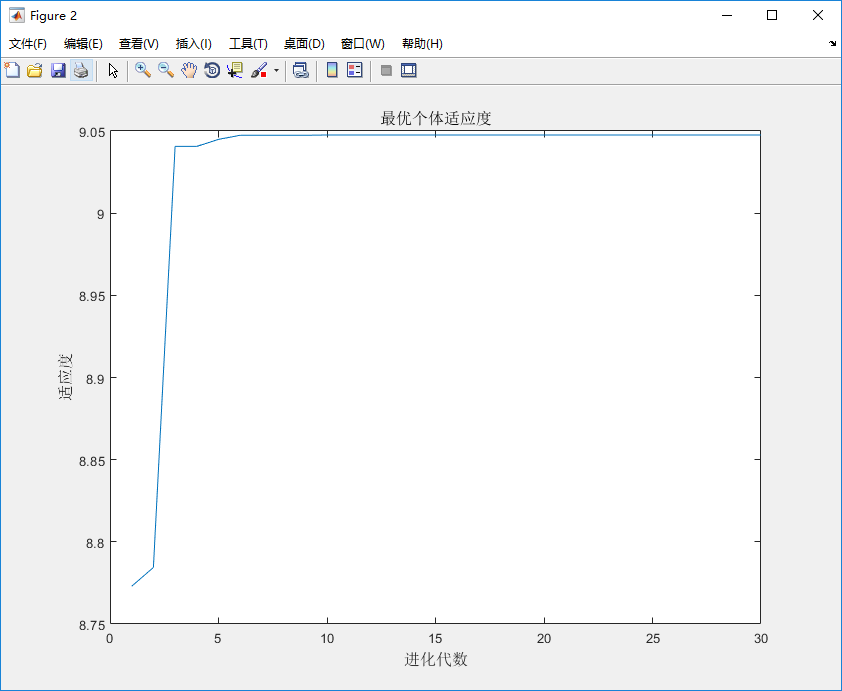
figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

main.m

function y = fun(x)
% 函数用于计算粒子适应度值
%x           input           输入粒子
%y           output          粒子适应度值
y = 2.1*(1-x+5*x.^3).*exp(-x.^2/2)-x.^2;

fun.m

实例分析2:

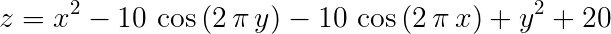
根据PSO算法思路求z最大值 ,其中x,y取值区间为[-5,5]

%% I. 清空环境
clc
clear

%% II. 绘制目标函数曲线
figure
[x,y] = meshgrid(-5:0.01:5,-5:0.01:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
surf(x,y,z)
shading flat;                           %去除网格线
hold on

%% III. 参数初始化
c1 = 1.49445;
c2 = 1.49445;

maxgen = 300;   % 进化次数
sizepop = 100;   %种群规模

Vmax = 1;
Vmin = -1;
popmax = 5;
popmin = -5;

%% IV. 产生初始粒子和速度
for i = 1:sizepop
    % 随机产生一个种群
    pop(i,:) = 5*rands(1,2);    %初始种群
    V(i,:) = rands(1,2);  %初始化速度
    % 计算适应度
    fitness(i) = fun(pop(i,:));   %染色体的适应度
end

%% V. 个体极值和群体极值
[bestfitness bestindex] = max(fitness);
zbest = pop(bestindex,:);   %全局最佳
gbest = pop;    %个体最佳
fitnessgbest = fitness;   %个体最佳适应度值
fitnesszbest = bestfitness;   %全局最佳适应度值

%% VI. 迭代寻优
for i = 1:maxgen

    for j = 1:sizepop
        w=1; %这里惯性因子w设为1，过小会导致局部最优 过大导致搜索粗糙 一般建议取0.6-0.75
        % 速度更新
        V(j,:) = w*V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax)) = Vmax;
        V(j,find(V(j,:)<Vmin)) = Vmin;

        % 种群更新
        pop(j,:) = pop(j,:) + V(j,:);
        pop(j,find(pop(j,:)>popmax)) = popmax;
        pop(j,find(pop(j,:)<popmin)) = popmin;

        % 适应度值更新
        fitness(j) = fun(pop(j,:));
    end

    for j = 1:sizepop
        % 个体最优更新
        if fitness(j) > fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end

        % 群体最优更新
        if fitness(j) > fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end
    yy(i) = fitnesszbest;
end
%% VII.输出结果
[fitnesszbest, zbest]
plot3(zbest(1), zbest(2), fitnesszbest,'r.','MarkerSize',20)
plot3(zbest(1), zbest(2), fitnesszbest,'ro','MarkerSize',16)
x_text=['x=',num2str(zbest(1))]; % x横坐标转换为字符串
y_text=['y=',num2str(zbest(2))];  % y横坐标转换为字符串
z_text=['z=',num2str(fitnesszbest)]; %全局最优值z转换为字符串
max_text=char('全局最优',x_text,y_text,z_text);  % 生成标志最大值点的字符串
text(zbest(1)+0.3,zbest(2)+0.3, fitnesszbest-1.4,max_text) %图上绘出全局最优的数据值
figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

main.m

function y = fun(x)
%函数用于计算粒子适应度值
%y           output          粒子适应度值
y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

fun.m

其中要注意的是惯性因子ω越大,粒子飞行的速度和位置更新的幅度就越大,偏离原先寻优轨道的程度也就越大,从而发现新的解域;相反,如果惯性因子ω越小,有利于局部寻优,提高搜索精度,惯性因子ω的大小决定了粒子对当前速度继承的多少.

所以实际操作中开始将惯性因子设置得较大,然后再迭代的过程中逐步减小,这样可以使得粒子群在开始优化时得到较大的解空间,后期逐渐收缩到较好的区域进行更精细化的搜索,以加快收敛与精度.

为了更好的平衡全局搜索与局部搜索,故提出线性递减惯性权重LDIW(linear decreasing inertia weight)

ω(k)=ω(start)-(ω(start)-w(end))(T(max)-k)/T(max)

其中ω(start)为初始惯性权重,一般取0.9,w(end)为迭代至最大次数时的惯性权重,一般取0.4,k为当前迭代次数,T(max)为最大迭代次数.

ws = 0.9;
we = 0.4;
maxgen = 300;
hold on;

for k = 1:maxgen
    w(k) = ws - (ws-we)*(k/maxgen);
end
plot(w,'linewidth',3);

for k = 1:maxgen
    w(k) = ws - (ws-we)*(k/maxgen)^2;
end
plot(w,'r-.','linewidth',3);

for k = 1:maxgen
    w(k) = ws - (ws-we)*(2*k/maxgen-(k/maxgen)^2);
end
plot(w,'k--.','linewidth',3);

for k = 1:maxgen
    w(k) = we * (ws/we)^(1/(1+10*k/maxgen));
end
plot(w,'--','linewidth',3);

legend('线性惯性权重递减','常用权重2','常用权重3','常用权重4')
xlabel('迭代次数')
ylabel('速度更新权重W')

速度更新权重ω的选择