BZOJ4823 [Cqoi2017]老C的方块【最小割】

题目

老C是个程序员。

作为一个懒惰的程序员，老C经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的R行C列网格上，如果两个小方格有公共的边，就称它们是相邻的，而且有些相邻的小方格之间的公共边比较特殊。特殊的公共边排列得有很强的规律。首先规定，第1行的前两个小方格之间的边是特殊边。然后，特殊边在水平方向上每4个小方格为一个周期，在竖直方向上每2个小方格为一个周期。所有的奇数列与下一列之间都有特殊边，且所在行的编号从左到右奇偶交替。

下图所示是一个R=C=8的网格，蓝色标注的边是特殊边。首先，在第1行，第1列和第2列之间有一条特殊边。因为竖直方向周期为2，所以所有的奇数行，第1列和第2列之间都有特殊边。因为水平方向周期为4，所以所有奇数行的第5列和第6列之间也有特殊边，如果网格足够大，所有奇数行的第9列和第10列、第13列和第14列之间都有特殊边。因为所有的奇数列和下一列之间都有特殊边，所以第3列和第4列、第7列和第8列之间也有特殊边，而所在行的编号从左到右奇偶交替，所以它们的特殊边在偶数行。如果网格的规模更大，我们可以用同样的方法找出所有的特殊边。

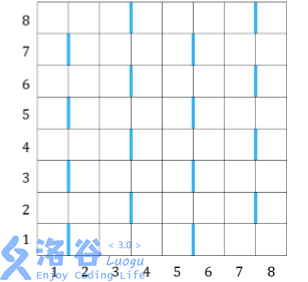
网格的每个小方格刚好可以放入一个小方块，在游戏的一开始，有些小方格已经放上了小方块，另外的小方格没有放。老C很讨厌下图所示的图形，如果他发现有一些小方块排列成了它讨厌的形状（特殊边的位置也要如图中所示），就很容易弃疗，即使是经过任意次旋转、翻转后排列成讨厌的形状，老C也同样容易弃疗。

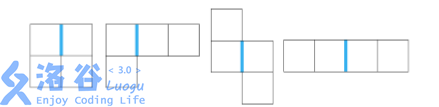
为了防止弃疗，老C决定趁自己还没有弃疗，赶紧移除一些格子里小方块，使得剩下的小方块不能构成它讨厌的形状。但是游戏里每移除一个方块都是要花费一些金币的，每个方块需要花费的金币有多有少参差不齐。老C当然希望尽可能少的使用游戏里的金币，但是最少要花费多少金币呢？老C懒得思考，就把这个问题交给你了。

输入格式

第一行有3个正整数C,R,n，表示C列R行的网格中，有n个小方格放了小方块。接下来n行，每行3个正整数x,y,w，表示在第x列第y行的小方格里放了小方块，移除它

需要花费w个金币。保证不会重复，且都在网格范围内。

输出格式

输出一行，包含一个整数，表示最少花费的金币数量。

输入样例

3 3 7

1 1 10

1 2 15

1 3 10

2 1 10

2 2 10

2 3 10

3 1 10

输出样例

提示

【输入输出样例 2 说明】如图所示。容易发现，如果不移除第1列第2行的

小方块，则至少要移除两个小方块，才能不包含老 C 讨厌的图形，花费至少20个金币；而删除第1列第2行的小方块后，原有的讨厌图形全都不存在了，只需要花费15个金币。

【数据规模与约定】

对于第 1~2 个测试点，1 ≤ C, R ≤ 100, 1 ≤ n ≤ 20；

对于第 3~6 个测试点，1 ≤ C, R ≤ 10^5, 2000 ≤ n ≤ 5000，数据有梯度；

对于第 7~10 个测试点，1 ≤ C, R ≤ 10^5, 30000 ≤ n ≤ 10^5，数据有梯度；

对于所有测试点，1 ≤ C, R, n ≤ 10^5, 1 ≤ w ≤ 10^4。

题解

又是一道神仙观察题，，，

观察图形，如果我们设与特殊边相邻的格子为中间格，与中间格相邻的其它格子成为相邻格

一个相邻格属于与它相邻的中间格

我们发现，一个图形不合法，当且仅当两个不属于同一个中间格的相邻格联通

考虑最小割解决

我们对图二分染色，

每个中间格和其相邻格，白点连边向黑点，流量inf

然后S向白点的相邻格连边，流量为费用

黑点的相邻格向T连边，流量为费用

然后相邻的两个中间格，其中的黑点向白点连边，流量为其中较小费用

为使所有相邻格不连通，要么去掉联通的相邻格的一个，此时割源汇点的边

要么直接去掉中间点的一个，此时割中间点的边

跑一遍最大流就可以求出了

#include<iostream>

#include<cstdio>

#include<algorithm>

#define LL long long int

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define REP(i,n) for (int i = 1; i <= (n); i++)

using namespace std;

const int maxn = 100005,maxm = 1000005,INF = 1000000000;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}

	return out * flag;

}

int h[maxn],ne = 2;

struct EDGE{int to,nxt,f;}ed[maxm];

inline void build(int u,int v,int w){

	ed[ne] = (EDGE){v,h[u],w}; h[u] = ne++;

	ed[ne] = (EDGE){u,h[v],0}; h[v] = ne++;

}

int q[maxn],head,tail,d[maxn],vis[maxn],cur[maxn],used[maxn],S,T,now;

bool bfs(){

	vis[S] = now; q[head = tail = 1] = S;

	int u;

	while (head <= tail){

		u = q[head++];

		Redge(u) if (ed[k].f && vis[to = ed[k].to] != now){

			d[to] = d[u] + 1; vis[to] = now;

			if (to == T) return true;

			q[++tail] = to;

		}

	}

	return vis[T] == now;

}

int dfs(int u,int minf){

	if (u == T || !minf) return minf;

	int flow = 0,f,to;

	if (used[u] != now) cur[u] = h[u],used[u] = now;

	for (int& k = cur[u]; k; k = ed[k].nxt)

		if (d[to = ed[k].to] == d[u] + 1 && (f = dfs(to,min(minf,ed[k].f)))){

			ed[k].f -= f; ed[k ^ 1].f += f;

			flow += f; minf -= f;

			if (!minf) break;

		}

	return flow;

}

int maxflow(){

	int flow = 0; now = 1;

	while (bfs()){

		flow += dfs(S,INF);

		now++;

	}

	return flow;

}

int N,M,n;

struct point{int x,y,w,c,id;}p[maxn];

inline bool cmp1(const point& a,const point& b){

	return a.x == b.x ? a.y < b.y : a.x < b.x;

}

inline bool cmp2(const point& a,const point& b){

	return a.y == b.y ? a.x < b.x : a.y < b.y;

}

void solve(){

	int t;

	sort(p + 1,p + 1 + n,cmp1);

	REP(i,n){

		t = (p[i].y + 2 * (p[i].x & 1)) % 4;

		if (p[i + 1].x != p[i].x || p[i + 1].y != p[i].y + 1) continue;

		if (t == 0) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

		if (t == 2) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

		if (t == 3) !p[i].c ? build(p[i].id,p[i + 1].id,min(p[i].w,p[i + 1].w)) : build(p[i + 1].id,p[i].id,min(p[i].w,p[i + 1].w));

	}

	sort(p + 1,p + 1 + n,cmp2);

	REP(i,n){

		t = (p[i].y + 2 * (p[i].x & 1)) % 4;

		if (p[i + 1].y != p[i].y || p[i + 1].x != p[i].x + 1) continue;

		if (t == 0) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

		if (t == 1) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

		if (t == 2) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

		if (t == 3) p[i].c ? build(p[i].id,p[i + 1].id,INF) : build(p[i + 1].id,p[i].id,INF);

	}

	printf("%d\n",maxflow());

}

int main(){

	N = read(); M = read(); n = read(); S = 0; T = n + 1;

	swap(N,M);

	int t;

	REP(i,n){

		p[i].id = i;

		p[i].x = read();

		p[i].y = read();

		swap(p[i].x,p[i].y);

		p[i].w = read();

		p[i].c = (p[i].x & 1) ^ (p[i].y & 1);

		t = (p[i].y + 2 * (p[i].x & 1)) % 4;

		if (t && t - 3) p[i].c ? build(S,i,p[i].w) : build(i,T,p[i].w);

	}

	solve();

	return 0;

}