Aho-Corasick自动机

在模式匹配问题中，如果模板有很多个,KMP算法就不太适合了。因为每次查找一个模板。都要遍历整个文本串。可不可以只遍历一次文本串呢？可以，方法是把所有模板组成一个大的状态转移图（称为$Aho-Corasick$自动机，简称$AC$自动机），而不是每个模板各建一个状态转移图。注意到KMP的状态转移图是线性的字符串加上失配边组成的，不难想到AC自动机是Trie加上失配边组成的。

下图是$\{he,she,his,hers \}$的Trie。

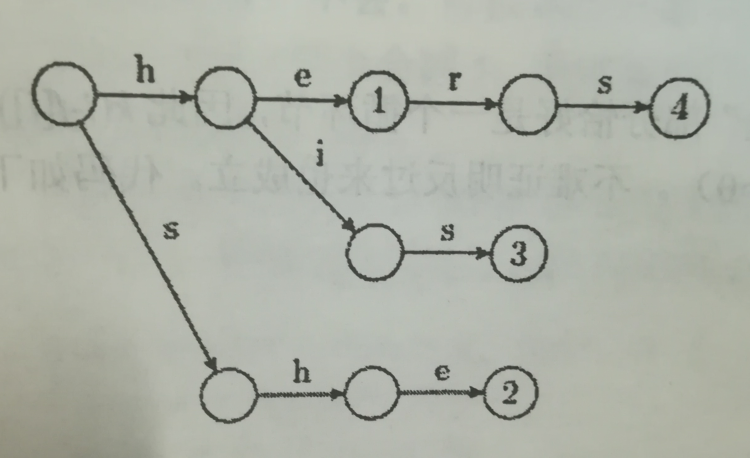
下图是对应的Aho-Corasick自动机。

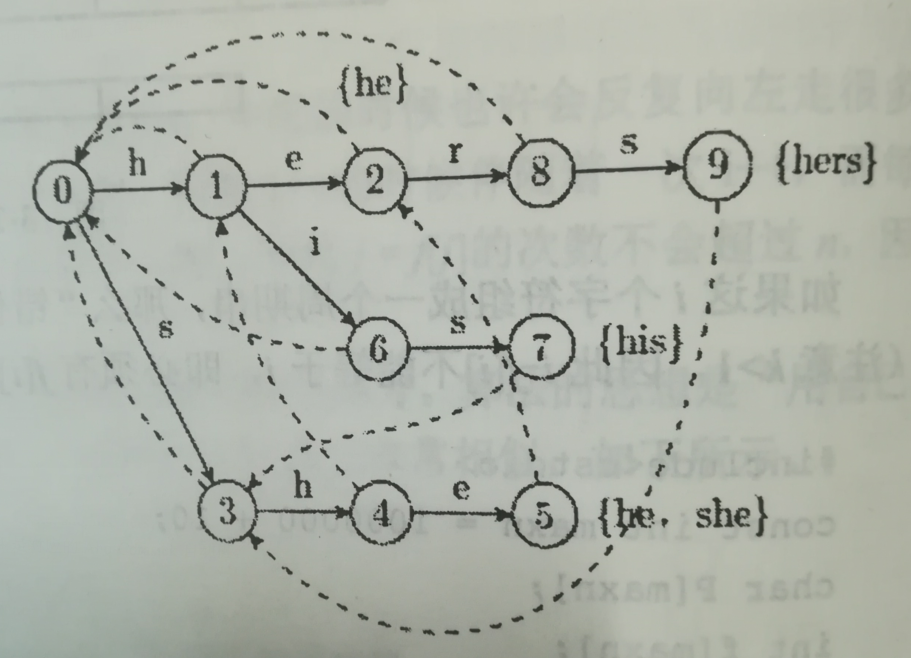
如果已经构造好AC自动机，匹配算法几乎和KMP是一样的，代码如下：

//在T中找模板
void find(const char* T)
{
        int n = strlen(T);
    int j = ;                //当前结点编号，初始为根节点
    for (int i = ; i < n; i++)   //文本串当前指针
    {
        int c = idx(T[i]);
        while (j && !ch[j][c])  j = f[j];    //顺着失配边走，直到可以匹配
        j = ch[j][c];
        if (val[j])  print(j);
        else  if (last[j])  print(last[j]);   //找到了
    }
}

其中print函数为：

//递归打印以结点j结尾的所有字符串
void print(int j)
{
    if (j)
    {
        printf("%d: %d\n",j, val[j]);
        print(last[j]);
    }
}

代码中出现了一个陌生的数组last，下面解释以下。和Trie一样，我们认为所有val[j]>0的结点都是单词结点，反之亦然。但和Trie不同的是，同一个结点可能对应多个字符串的结尾，如图所示：

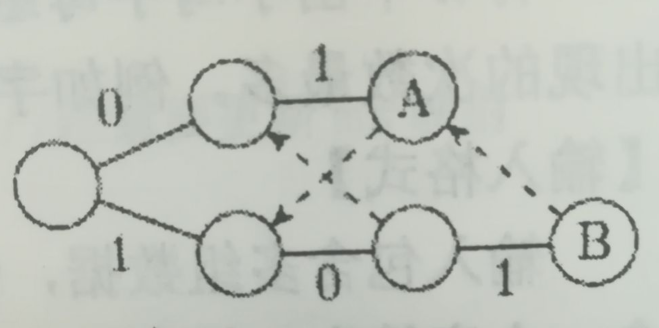
结点B不仅意味着找到串101，还意味着找到串01。换句话说，当找到一个模板后，应该顺着失配指针往回走，，看看有没有其它串。当然，失配指针不一定指向一个单词结点（比如，两个串是101和010，那么上图的结点A不是单词结点），为了提高效率，这里增设一个指针last[j]，表示结点j沿着失配指针往回走时，遇到的下一个单词结点编号。这个last[j]在正规文献中叫后缀链接(suffix link)。

计算失配函数的方式和KMP很接近，只是把线性递归改成了按照BFS顺序递推，代码如下：

//计算fail函数
void getFail()
{
    queue<int>q;
    f[] = ;
    //初始化队列
    for (int c = ; c < sigma_size; c++)
    {
        int u = ch[][c];
        if (u)
        {
            f[u] = ;
            q.push(u);
            last[u] = ;
        }
    }
    //按BFS序计算fail
    while (!q.empty())
    {
        int r = q.front(); q.pop();
        for (int c = ; c < sigma_size; c++)
        {
            int u = ch[r][c];
            if (!u)  continue;
            q.push(u);
            int v = f[r];
            while (v && !ch[v][c])  v = f[v];
            f[u] = ch[v][c];
            last[u] = (val[f[u]] ? f[u] : last[f[u]]);
        }
    }
}

由于失配工程比较复杂，要反复沿着失配边走，在实践中常常会把上述AC自动机改造一下，把所有不存在的边补上，即把计算失配函数中的语句"if(!u)  continue;"改成：if(!u){ ch[r][c] = ch[f[r]][c]; continue;}

这样，就完全不需要失配函数了，而是对所有的转移一视同仁也就是说，find函数中的语句"while(j && !ch[j][c])  j=f[j];"; 可以直接完全删除。