aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAADdpJREFUeJzt3W2MXOdZh/HrXztpUZomH7JIwTZNJFxSq1QEVqZSEQQlBScgG6SAbFEoEGpVwrSoBdUQlICrSrSRKAIZqEWi0qpNCA0vFnHl8pKqgHDwpk2T2K7RYijeuCKbNA1EEQSTmw87LqPN7M6Z9diz+/T6SSvNOfPMmXut9ZXx2ZmTVBWSpLa8YtIDSJLGz7hLUoOMuyQ1yLhLUoOMuyQ1yLhLUoOGxj3JPUmeSvLEEvcnyW8nmU3yWJLvGP+YkqRRdHnl/hFg2zL33wxs7n3tBn7v/MeSJJ2PoXGvqs8CX1lmyQ7go7XgCHBlkqvHNaAkaXTrx3CMDcDpvu253r4vL16YZDcLr+657LLLvvO6665b0RM+/uRzfNuGK1b02PN5jseffA5gyedebq5Bj13J93HuMeeO13/MpfYtXi+tRoN+jpda1/XneZS/b/33L7V2XO05n+M88sgjT1fV1LB144h7BuwbeE2DqjoAHACYnp6umZmZFT3hNXsfZOY3fnBFjz2f57hm74MASz73cnMNeuxKvo9zjzl3vP5jLrVv8XppNRr0c7zUuq4/z6P8feu/f6m142rP+RwnyZe6rBvHu2XmgE192xuBM2M4riRphcYR94PAT/beNfMm4LmqetkpGUnSxTP0tEySe4EbgKuSzAF3ApcAVNXvA4eAW4BZ4AXgpy/UsJKkbobGvap2Dbm/gJ8b20SSpPPmJ1QlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUGd4p5kW5KTSWaT7B1w/zcneSjJ55M8luSW8Y8qSepqaNyTrAP2AzcDW4BdSbYsWvarwP1VdT2wE/jdcQ8qSequyyv3rcBsVZ2qqheB+4Adi9YU8Jre7SuAM+MbUZI0qi5x3wCc7tue6+3r92vAW5PMAYeAnx90oCS7k8wkmZmfn1/BuJKkLrrEPQP21aLtXcBHqmojcAvwsSQvO3ZVHaiq6aqanpqaGn1aSVInXeI+B2zq297Iy0+73AbcD1BV/wC8CrhqHANKkkbXJe5Hgc1Jrk1yKQu/MD24aM2/ATcCJHk9C3H3vIskTcjQuFfVWWAPcBg4wcK7Yo4l2Zdke2/Ze4C3J/kCcC/wU1W1+NSNJOkiWd9lUVUdYuEXpf377ui7fRx483hHkyStlJ9QlaQGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJalCnuCfZluRkktkke5dY82NJjic5luQT4x1TkjSK9cMWJFkH7AfeAswBR5McrKrjfWs2A78MvLmqnk3yjRdqYEnScF1euW8FZqvqVFW9CNwH7Fi05u3A/qp6FqCqnhrvmJKkUXSJ+wbgdN/2XG9fv9cBr0vy90mOJNk26EBJdieZSTIzPz+/soklSUN1iXsG7KtF2+uBzcANwC7gD5Jc+bIHVR2oqumqmp6amhp1VklSR13iPgds6tveCJwZsObPq+p/qupfgJMsxF6SNAFd4n4U2Jzk2iSXAjuBg4vW/BnwfQBJrmLhNM2pcQ4qSepuaNyr6iywBzgMnADur6pjSfYl2d5bdhh4Jslx4CHgl6rqmQs1tCRpeUPfCglQVYeAQ4v23dF3u4B3974kSRPmJ1QlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUHGXZIaZNwlqUGd4p5kW5KTSWaT7F1m3a1JKsn0+EaUJI1qaNyTrAP2AzcDW4BdSbYMWHc58E7g4XEPKUkaTZdX7luB2ao6VVUvAvcBOwasex/wQeC/xjifJGkFusR9A3C6b3uut+9rklwPbKqqv1juQEl2J5lJMjM/Pz/ysJKkbrrEPQP21dfuTF4BfAh4z7ADVdWBqpququmpqanuU0qSRtIl7nPApr7tjcCZvu3LgTcAn0nyr8CbgIP+UlWSJqdL3I8Cm5Ncm+RSYCdw8NydVfVcVV1VVddU1TXAEWB7Vc1ckIklSUMNjXtVnQX2AIeBE8D9VXUsyb4k2y/0gJKk0a3vsqiqDgGHFu27Y4m1N5z/WJKk8+EnVCWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhrUKe5JtiU5mWQ2yd4B9787yfEkjyX56ySvHf+okqSuhsY9yTpgP3AzsAXYlWTLomWfB6ar6o3AJ4EPjntQSVJ3XV65bwVmq+pUVb0I3Afs6F9QVQ9V1Qu9zSPAxvGOKUkaRZe4bwBO923P9fYt5TbgU4PuSLI7yUySmfn5+e5TSpJG0iXuGbCvBi5M3gpMA3cNur+qDlTVdFVNT01NdZ9SkjSS9R3WzAGb+rY3AmcWL0pyE3A78L1V9d/jGU+StBJdXrkfBTYnuTbJpcBO4GD/giTXAx8GtlfVU+MfU5I0iqFxr6qzwB7gMHACuL+qjiXZl2R7b9ldwKuBP07yaJKDSxxOknQRdDktQ1UdAg4t2ndH3+2bxjyXJOk8+AlVSWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWqQcZekBhl3SWpQp7gn2ZbkZJLZJHsH3P/KJH/Uu//hJNeMe1BJUndD455kHbAfuBnYAuxKsmXRstuAZ6vqW4APAR8Y96CSpO66vHLfCsxW1amqehG4D9ixaM0O4A97tz8J3Jgk4xtTkjSKVNXyC5JbgW1V9bO97Z8Avquq9vSteaK3Zq63/c+9NU8vOtZuYHdv81uBk+P6Ri6Aq4Cnh65afdbi3M58cazFmWFtzn0hZ35tVU0NW7S+w4EGvQJf/F+ELmuoqgPAgQ7POXFJZqpqetJzjGotzu3MF8danBnW5tyrYeYup2XmgE192xuBM0utSbIeuAL4yjgGlCSNrkvcjwKbk1yb5FJgJ3Bw0ZqDwNt6t28F/qaGne+RJF0wQ0/LVNXZJHuAw8A64J6qOpZkHzBTVQeBu4GPJZll4RX7zgs59EWyJk4fDbAW53bmi2Mtzgxrc+6Jzzz0F6qSpLXHT6hKUoOMuyQ1yLgvI8n7kjyW5NEkn07yTZOeaZgkdyX5Ym/uP01y5aRn6iLJjyY5luSlJKv6bW/DLsex2iS5J8lTvc+jrAlJNiV5KMmJ3s/FuyY9UxdJXpXkH5N8oTf3r09sFs+5Ly3Ja6rqP3q33wlsqap3THisZSX5fhberXQ2yQcAquq9Ex5rqCSvB14CPgz8YlXNTHikgXqX4/gn4C0svAX4KLCrqo5PdLBlJPke4Hngo1X1hknP00WSq4Grq+pzSS4HHgF+eDX/OQP0Ppl/WVU9n+QS4O+Ad1XVkYs9i6/cl3Eu7D2XMeCDWatNVX26qs72No+w8LmEVa+qTlTVav7E8jldLsexqlTVZ1ljnzupqi9X1ed6t/8TOAFsmOxUw9WC53ubl/S+JtIN4z5EkvcnOQ38OHDHpOcZ0c8An5r0EI3ZAJzu255jDURnLetdZfZ64OHJTtJNknVJHgWeAv6yqiYy99d93JP8VZInBnztAKiq26tqE/BxYM/yR7s4hs3cW3M7cJaFuVeFLnOvAZ0utaHxSPJq4AHgFxb9S3rVqqr/rapvZ+FfzVuTTORUWJdryzStqm7quPQTwIPAnRdwnE6GzZzkbcAPATeupk8Kj/BnvZp1uRyHxqB3zvoB4ONV9SeTnmdUVfXVJJ8BtgEX/ZfZX/ev3JeTZHPf5nbgi5Oapask24D3Atur6oVJz9OgLpfj0Hnq/WLybuBEVf3mpOfpKsnUuXeoJfkG4CYm1A3fLbOMJA+wcGnil4AvAe+oqicnO9XyepeAeCXwTG/XkdX+Dh+AJD8C/A4wBXwVeLSqfmCyUw2W5Bbgt/j/y3G8f8IjLSvJvcANLFyG9t+BO6vq7okONUSS7wb+Fnichb9/AL9SVYcmN9VwSd7Iwv/bYh0LL57vr6p9E5nFuEtSezwtI0kNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkN+j9s+sEIFmBC4AAAAABJRU5ErkJggg==" alt="" />
seaborn实现柱状图和热力图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df=sns.load_dataset('flights')#通过在线的repository(存储库)下载数据,sns的内置方法
print(df.head())
df.shape
结果:
year month passengers
0 1949 January 112
1 1949 February 118
2 1949 March 132
3 1949 April 129
4 1949 May 121
(144, 3)
df=df.pivot(index='month',columns='year',values='passengers')#生成透视表,阅读数据更加方便
print(df)
结果:
year 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 \
month
January 112 115 145 171 196 204 242 284 315 340 360
February 118 126 150 180 196 188 233 277 301 318 342
March 132 141 178 193 236 235 267 317 356 362 406
April 129 135 163 181 235 227 269 313 348 348 396
May 121 125 172 183 229 234 270 318 355 363 420
June 135 149 178 218 243 264 315 374 422 435 472
July 148 170 199 230 264 302 364 413 465 491 548
August 148 170 199 242 272 293 347 405 467 505 559
September 136 158 184 209 237 259 312 355 404 404 463
October 119 133 162 191 211 229 274 306 347 359 407
November 104 114 146 172 180 203 237 271 305 310 362
December 118 140 166 194 201 229 278 306 336 337 405
year 1960
month
January 417
February 391
March 419
April 461
May 472
June 535
July 622
August 606
September 508
October 461
November 390
December 432
结果:
<matplotlib.axes._subplots.AxesSubplot at 0xacac7f0>
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZsAAAEZCAYAAABB4IgrAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3XmcXFWZ//HPN93ZQ8K+RwJM2IWwizrIpoO4AAoDuIHgL+OKKOi4KziKjgsCLogBBAVZRAZwlGUwQQHZCUlYBAYiRBh2AgFCku7n98c9nVQ6vdx01amu2/m+ed1X37p166nTFbqfPueeex5FBGZmZjkNG+wGmJnZ0OdkY2Zm2TnZmJlZdk42ZmaWnZONmZll52RjZmbZOdmYmVl2TjZmZpadk42ZmWXXPtgNGEpGjpqYZTmGYcrzN8G6YyZkibvWiPFZ4gKs2T42S9wRassSd5Nh47LEBdg0RmSJu9HiLGFZp2NJnsDAhLZFWeJO2vLZLHEB1pt+veqNsfiZh0v9zhm+9mZ1v1e9nGzMzKqqs2OwW1Cak42ZWVVF52C3oDQnGzOzqup0sjEzs8zCPRszM8su46SLRmv5qc+SFgx2G8zMWlJnR7mtBEmrS/qtpPsl3SdpD0lrSrpW0oPp6xrpXEk6TdJDkmZJ2qm/+C2fbAaDlGkerJlZI0Vnua2cU4GrImIrYAfgPuALwHURMRm4Lj0GeDswOW1TgZ/1F7wSyUbSOEnXSbpT0mxJB6bjk1IG/oWkeyRdI2l0em6GpF3S/tqS5ta85i8p1p2S3piO7yVpuqQLgNmSvinp0zVt+JakY5v9vZuZ9aqzs9zWD0njgT2BswAiYlFEvAAcCJybTjsXOCjtHwicF4WbgdUlbdDXe1Qi2QALgYMjYidgb+AHkrpuUpoM/CQitgVeAN7bT6yngLemWIcBp9U8txvw5YjYhuJDPxJA0jDgcOD87sEkTZV0u6TbOzo84mdmzRPRWWqr/T2VtqndQm0GPA2cI+kuSdMkjQXWi4gniveKJ4B10/kbAY/VvH5eOtarqkwQEPBtSXsCnRTf1HrpuUciYmbavwOY1E+s4cCPJU0BOoAtap67NSIeAYiIuZKelbRjeq+7ImKF24kj4kzgTMi3goCZWY9KTn2u/T3Vi3ZgJ+BTEXGLpFNZNmTWk55WJOjz919Vks37gXWAnSNicRoSG5Wee63mvA5gdNpfwrKe26iacz4DPEkxJjmMotfU5eVu7zsNOApYHzi7ru/AzKzROhq2ttA8YF5E3JIe/5Yi2TwpaYOIeCINkz1Vc/7EmtdvDDze1xtUZRhtAvBUSjR7A5uUeM1cYOe0f0i3WE9EMUH9g0BfkwEuA/YHdgWuXtlGm5ll1aAJAhHxf8BjkrZMh/YF7gWuIF1OSF8vT/tXAB9Ks9LeAMzvGm7rTUv3bCS1U/RczgeulHQ7MBO4v8TLvw9cLOmDwJ9qjv8UuFTSocB0VuzNLBURiyRNB16IiOosQmRmq4bGriDwKeB8SSOAh4EPU3RILpZ0DPAocGg69w/AAcBDwCvp3D4ponUvM0jaAfhFROw2SO8/DLgTODQiHuzvfK/6XPCqz8t41edlvOrz8hqx6vNrc64t9Ttn5HZvHfRVn1t2GE3SR4HfAF8ZpPffhiJrX1cm0ZiZNV2Dpj43Q8sOo0XEGcAZg/j+91JMBzQza0nRmakbmkHLJpsqah+WZyhmxLA8/0xtmYaOXlj8MuuOyDNEl8uCjtf6P2kA7ul4jc2Hr54l9uK+Z5oO2IJheUZcFgxrZ3xnnjarY3iWuAueHtX/SQO0Xv+n9K9Fei1lONlYw1Ut0eSUK9FUUa5Es0rzqs9mZpadK3WamVl27tmYmVl2vmZjZmbZVah4mpONmVlVVahnM+g3dUrqkDSzZpvUx7l7Sfp981pnZta6IjpKba2gFXo2r0bElEYGlNRWz1pmktojojr9UzNbNblnUx9JbZK+J+m2VN/632qeHi/pMkn3SjojrV+GpAWSTpJ0C7CHpLmS1k7P7SJpRtrfTdJNqUDQTV2rnEo6StIlkq4ErpH0q66KoOn58yW9u1mfgZlZvxpbFjqrVujZjJbUVfzskYg4GDiGYsnqXSWNBG6UdE06ZzdgG+DvwFXAeyhqL4wF5kTE1wCWFfJcwf3AnhGxRNJ+wLdZVt1zD2D7iHhO0lsoat9cLmkC8EaWLbW9VKp4NxVgxPA1aW9fbaCfg5nZyqlQz6YVkk1Pw2hvA7aX1FWHZgJF+edFFNU0HwaQ9BvgzRTJpgO4tMT7TQDOlTSZorJc7ToX10bEcwARcb2kn0halyKhXdrT0FptBbyxYyb5Fmkzax7PRqubKMqTLlewTNJerFh6tOvxwm7XaXqr1PlNYHpEHJwmI8yoea57bZtfUVQJPRw4eqW+AzOz3FpkiKyMlrxmQ1EV82OShgNI2kJSVyGT3SRtmq7VHAbc0EuMuSyr1PnemuMTgH+k/aP6accvgeMAIuKelWi/mVl+FSox0KrJZhpFSdI7Jc0Bfs6yXthfge8Ac4BHKEo39+RE4FRJf6EYYuvyn8DJkm6k75LQRMSTwH3AOQP8PszM8qlQshn0YbSIWKGUYUR0Al9KW60ZLD/s1WuciPgLsEUP5/212/GvpuO/pOjJLCVpDMW1ot/09T2YmQ0KD6NVX5qpdj9wekTMH+z2mJmtoGNJua0FDHrPplVFxP8ArxvsdpiZ9apFhsjKcLIxM6uqCg2jOdk00JjhI7PEHdmWp+Tt2iPGZ4k7elie9gJMastz02xnngrZbMiIPIGBzTKVn98kXs0Sd/iwfL8YN9wsz0j38DGtsa5Yr9yzMTOz7JxszMwsu6jOoiVONmZmVbWkNWaaleFkY2ZWVZ4gYGZm2VXomk1lb+qUFJJ+VfO4XdLTjarkKWmGpF0aEcvMLIuIclsLqHLP5mVgO0mjI+JV4K0sW2CzFFfkNLNKc8+maf4IvCPtH0HNGmZlK3KmY5+XNFvS3ZK+UxP/UEm3SnpA0j836XsyMyvHC3E2zYXA19LQ2fbA2UBXUihbkfPtwEHA7hHxiqQ1a+K3R8Rukg4Avg7s170BtZU6x41al1EjVm/8d2lm1oPoaPGbTmtUOtlExKxUAO0I4A/dni5VkZMigZwTEa+kmM/VnPe79PUOYFIvbVhaqXOdCVu2xuComa0aWqTXUkbVh9EArgC+z4plALoqcm4HvIvlq3XWVuQUK1b/7PJa+tpBxROzmQ1B0VluawFDIdmcDZwUEbO7HS9bkfMa4OhUu4Zuw2hmZq2rM8ptJUiam65dz5R0ezq2pqRrJT2Yvq6RjkvSaZIekjRL0k79xa98somIeRFxag9PlarIGRFXUfSObpc0EzghT0vNzBqs8RME9o6IKRHRddvHF4DrImIycF16DPB2isKSkymuWf+sv8CVHRrqpcLnDFIlz5WpyBkR36EoNV17bK+a/Wfo5ZqNmdmgyT9B4EBgr7R/LsXv139Px8+LiABulrS6pA0i4oneAlW+Z2Nmtsoq2bORNFXS7TXb1B6iBXCNpDtqnl+vK4Gkr+um4xsBj9W8dl461qvK9mzMzFZ5Ja/H1M6a7cObIuJxSesC10q6v49z1dPb9BXcPRszs6pq4Gy0iHg8fX0KuAzYDXhS0gYA6etT6fR5wMSal28MPN5XfPdsGigyrUG0pDPPuOwrHa/1f9IAtCnf3zC5JnEuyjQ9dJh6+gOwMTp6/OOyfos68/z75YoLsPjVPKVWx+88qv+TBlPJnk1/JI0FhkXES2n/bcBJFJOnjqS4pn0kcHl6yRXAJyVdCOwOzO/reg042ZiZVVY07qbO9YDLVPxx1A5cEBFXSboNuFjSMcCjwKHp/D8ABwAPAa8AH+7vDZxszMyqqkGz0SLiYWCHHo4/C+zbw/EAPrEy7+FkY2ZWVQ0aRmsGJxszs6qq0NpoTjZmZlVVoZ7NkJ76LOngVNFzqwG8dpqkbdL+XElrN76FZmZ18EKcLeMI4Abg8JV5kaS2iPhIRNybp1lmZg3QwIU4cxuyyUbSOOBNwDGkZCNpL0l/lnSZpHslnSEVN4VIWiDpJEm3AHtImiFpl97fwcxscMWSjlJbKxiyyYai+uZVEfEA8FzNEti7AccDrwc2B96Tjo8F5kTE7hFxQ9k3qV1zaOGi+Q1svplZP9yzaQlHUJSNJn09Iu3fGhEPR0QHRcG1N6fjHcClK/smEXFmROwSEbuMGjGh3jabmZVXoWs2Q3I2mqS1gH2A7SQFRT2boLjrtXua73q8MCUgM7NqaJFeSxlDtWdzCEWthU0iYlJETAQeoejF7CZp03St5jCKCQRmZpUTnVFqawVDNdkcQbFqaa1LgfcBf6VYVG4ORQLqfp6ZWTUs6Si3tYAhOYxWW2Wz5thpkmYBJ0TEYT08P67b471q9ic1vpVmZnVqkV5LGUMy2ZiZrRKcbFpTRMygqKFtZlZ5uWpo5bBKJRszsyHFPZtV06KOJVnidmRa2XXE6Dz//MMyVZAEWJzpnoERmaqLDsv4u6Ct75LvAzZiWKbPuC3fheqx6yzKElejx/V/0mBysjEzs9xiSWvcsFmGk42ZWVVVJ9c42ZiZVVWr3LBZhpONmVlVOdmYmVl2FRpGG6rL1SyVKnX+quZxu6SnJf1+MNtlZlavKq2Ntir0bF6mWP15dES8CrwV+Mcgt8nMrG6xpDUSSRlDvmeT/BF4R9o/gqKODQCSdpN0k6S70tct0/G/SJpSc96NkrZvaqvNzPrSWXJrAatKsrkQOFzSKGB74Jaa5+4H9oyIHYGvAd9Ox6cBRwFI2gIYGRGzugeurdS5aMmLGb8FM7PlVah22qqRbFKSmETRq/lDt6cnAJdImgOcAmybjl8CvFPScOBo4Je9xF5aqXNE+/gMrTcz60WFejarwjWbLlcA3wf2AtaqOf5NYHpEHCxpEmmhzoh4RdK1wIHAvwK7NLGtZmb9apVeSxmrUrI5G5gfEbMl7VVzfALLJgwc1e0104Argb9ExHPZW2hmthIiz3KMWawSw2gAETEvIk7t4an/BE6WdCPQ1u01dwAvAuc0oYlmZiulStdshnzPpnsFznRsBsuGy/4KbFHz9Fe7diRtSJGQr8naSDOzAWiVRFLGKtOzWVmSPkQxa+3LEVX6JzWzVUao3NYChnzPZqAi4jzgvMFuh5lZb6r0Z7CTjZlZRUVna/RaynCyaaAxw0fmids+KkvcdrX1f9IAbNi+Wpa4AOOU53/ZNTP9KExenO+XwXYj52eJu8EWeW5ObhuX77MYvtmaWeK27b5zlriN0tnR2M9UUhtwO/CPiHinpE0pbopfE7gT+GBELJI0kmLkZ2fgWeCwiJjbV2xfszEzq6gMs9E+DdxX8/i7wCkRMRl4HjgmHT8GeD4i/oniZvjv9hfYycbMrKKiU6W2MiRtTLGG5LT0WMA+wG/TKecCB6X9A9Nj0vP7pvN75WRjZlZREeW22jUc0za1h3A/Aj7PsgVu1gJeiFh66+g8YKO0vxHwWNGGWALMZ/mVWVbgazZmZhVVttcSEWcCZ/b2vKR3Ak9FxB01K6z0FDxKPNcjJxszs4pq4ASBNwHvlnQAMAoYT9HTWV1Se+q9bAw8ns6fB0wE5klqp1j2q88lvUonG0lvpFg5eelr0r0oLU3Sgp5WETAzq7pGTX2OiC8CXwRIPZsTIuL9ki4BDqGYkXYkcHl6yRXp8V/T83+KiPp7Nqms8ubATKCjq334pkczs0ET+VcH+HfgQkn/AdwFnJWOnwX8StJDFD2aw/sLVLZnswuwTX+Zq1XVZOp3psc/Bm6PiF9Kmksxq+JdwHDg0Ii4X9JY4HTg9RSf0zci4vKe4puZDYYcKwh0WzvyYWC3Hs5ZCBy6MnHLzkabA6y/MoEr5pmI2An4GXBCOvZliq7hrsDewPdSAjIzawmdoVJbK+izZyPpSorhstWAeyXdCrzW9XxEvDtv85rmd+nrHcB70v7bKC6YdSWfUcDrWP6GJ9IUwqkAq41enzEjVs/fWjMzmjKM1jD9DaN9vymtyG8Jy/fiuq//0pVAO1j2mQh4b0T8ra/AtVMK119960oOM5pZNTV6uZqc+hxGi4jrI+J64ICu/dpjzWliQ/wd2EbSSEkTgH1LvOZq4FNdd8VK2jFnA83MVlYjVxDIrew1m7f2cOztjWxIDmn+92sR8RhwMTALOJ9iVkV/vkkxYWCWpDnpsZlZyxhK12w+Bnwc2EzSrJqnVgNuytmwBtkW+F+AiPg8xVIMy4mISTX7twN7pf1XgX9rRiPNzAZiKF2zuQD4I3Ay8IWa4y9FRJ93iw42SR8FjgWOG+y2mJnlUKWbUfpMNhExn2KBtSNSnYP10mvGSRoXEY82oY0DEhFnAGcMdjvMzHJplSGyMsquIPBJ4BvAkyxbETSA7fM0y8zM+tPZIhf/yyi7gsBxwJYR8WzOxlTd6LYRWeJOaB+TJe7qbaOzxB2TqZom5Kuo+boleaptbDlsQZa4AOtMfClL3JFbj88Sd9h6eappAgzbPs9k0fbdW/tWwiHXs6GoW5CnBq2ZmQ3IUJog0OVhYIak/2b5FQR+mKVVZmbWr6HYs3k0bSPSZmZmg6xCk9HKJZuIOBFA0mrFw8g3EG1mZqV0dOa51phDqZZK2k7SXRSrP98j6Q5J2+ZtmpmZ9aWz5NYKyqbFM4HPRsQmEbEJcDzwi3zNykNSnz0ySTMk7dKs9piZ1SNQqa0VlL1mMzYipnc9iIgZru1iZja4Oit00aZsz+ZhSV+VNCltXwEeydmwXCTtJen3NY9/LOmobuccI+mUmsf/T5Jn3plZS+lEpbZWUDbZHA2sA1xKUWhsbeCoTG1qBRdSFE4bnh5/GDhnENtjZraCKg2jlU02mwMT0/nDKerB/DlXowZbRLwM/Al4p6StgOERMbuncyVNlXS7pNtfWugFFsyseTpQqa0VlL1mcz5wAsVstFaZ3DBQ/VXt7DIN+BJwP330amordW661g4VGkE1s6qr0i/jssnm6Yi4MmtLmmdp1U6KRLMvcEP3kyLiFkkTgZ3wgqNm1oKGYrL5uqRpwHUsv1zN77K0KoPaqp2Suqp2PkjfVTsvBqZExPPNaKOZ2cpolesxZZRNNh8GtqK4XlNbYqAyyYZyVTv36nbozcAp3c8zM2sFFaowUDrZ7BARr8/akoxWtmqnpNWBW4G7I+K6nG0zMxuoVpnWXEbZZHOzpG0i4t6srclkZat2RsQLwBb5WmRmVr+OwW7ASiibbN4MHCnpEYprNqJYkNMXzs3MBkmnhl7PZv+srbAhZQxt2WKPzFS/Y1Gmn9kFi4b3f9IALXktz4q/Gpbnw9C4jCtcjcpTzTZefiFLXKC4Nb5OVbrXomyJgb/nboiZma2coTj12czMWsxQnI1mZmYtplWWoinDycbMrKLcszEzs+yqdM2mOgWszcxsOVFy64+kUZJulXS3pHsknZiObyrpFkkPSrpI0oh0fGR6/FB6flJ/71GpZCPpYEmRlv1v1nseJynPvEozszp0qtxWwmvAPhGxAzAF2F/SG4DvAqdExGTgeeCYdP4xwPMR8U8US3p9t783qFSyAY6gWKH58Ca+53GAk42ZtZzOklt/orAgPRyetgD2AX6bjp8LHJT2D0yPSc/vK/V9h2llko2kccCbKDLq4elYryWeJR0g6X5JN0g6res8Sd+QdELNa+akUtdjJf136kbOkXSYpGOBDYHpkqY377s1M+tfh8pttUUe0za1eyxJbZJmAk8B11IsXPxCRCxJp8wDNkr7GwGPAaTn5wNr9dXWKk0QOAi4KiIekPScpJ16O1HSKODnwJ4R8Yik35SIvz/weES8I8WYEBHzJX0W2DsinunlvaYCUwHWGrMRq43q8/M2M2uYshMEaos89nFOBzAlLUR8GbB1T6elrz31Yvq8PFSZng3FENqFaf/C9Lg3WwEPR8Qj6XGZZDMb2E/SdyX9c0TML9OoiDgzInaJiF2caMysmRo1jFYrLUQ8A3gDsHqqBQawMfB42p8HTISltcImAM/1FbcSyUbSWhRjh9MkzQU+BxxGsehpTyWe+xo77LEsdEQ8AOxMkXROlvS1hjTezCyTBs5GWyf1aJA0GtgPuA+YDhySTjsSuDztX5Eek57/U0QMiZ7NIcB5EbFJREyKiIlAV69lmzQNbwJFiWeA+4HNaqbjHVYTay5FqWfSUNymaX9D4JWI+DXw/a5zgJeA1XJ8U2Zm9WjgbLQNKK5NzwJuA66NiN8D/w58VtJDFNdkzkrnnwWslY5/FvhCf29QlWs2RwDf6XbsUuB9FKWblyvxHBGvSvo4cJWkZygKodW+7kPpQthtwAPp+OuB70nqBBYDH0vHzwT+KOmJiNi74d+ZmdkANeqmzoiYBezYw/GHgd16OL4QOHRl3qMSyaaHcs1ExGk1D1co8QxMj4it0nS8nwC3p9e9Cryth/PnAlf38D6nA6evfKvNzPKqUvG0qgyjDcT/S72XeyguXv18kNtjZtZQDRxGy64SPZuBiIhTKO5sNTMbkqq0NtqQTTaD4dWORVnijmzLE/flzjxx5+mVLHEBFg8b1f9JA7CgLU9FzQntI7PEBRjx6BqZIj+fJ+yN9+eJC0zY/dEscWPLWVniAoz4RK+3CpY25Cp1mplZ6+msULpxsjEzq6gqTRBwsjEzqyhfszEzs+xaZaZZGU42ZmYV5Ws2ZmaWXXVSTeabOiV9OZUYnSVppqTdBxBjL0lvbGCb5kpau1HxzMwGS45Vn3PJ1rORtAfwTmCniHgt/YIfMYBQewELgJsa2LwBkdReU0jIzGxQdVSob5NzGG0D4JmIeA2gq/iYpJ2BHwLjgGeAoyLiCUkzgJkUi76NB46mqBj3UaBD0geAT1Gs6HwG8Lr0PsdFxI2SvkGxgvMGwBYUK5G+AXg78A/gXRGxOL3mc5K6FtV8X0Q8JGmdPuJuCExK7X1foz4gM7N6tEqvpYycw2jXABMlPSDpp5LeImk4xaKWh0TEzsDZwLdqXjM2It4IfBw4OyLmUiSAUyJiSkT8BTg1Pd4VeC8wreb1mwPvoKiP/WuKxThfD7yajnd5MSJ2A34M/Cgd6yvuzsCBEbFCoqktt/rKohdW+kMyMxuoTqLU1gqy9WwiYkHqxfwzsDdwEfAfwHbAtcVizLQBT9S87DfptX+WNL6rmE83+1HUsOl6PF5SV72ZP0bEYkmzU+yr0vHZFD2T5d4nfe1aP62vuFek1aJ7+j6Xlltdf/WtW+Nf1cxWCVX6hZN1NlqqaT0DmJESwCeAeyJij95e0s9jKHpje3T/5Z+SRNeQXaekxTWV4zpZ/nuNHvb7ivtyL+01Mxs0HkYDJG0paXLNoSkUZUbXSZMHkDRc0rY15xyWjr8ZmB8R81mxUuY1wCdr3mfKAJp3WM3XvzYwrplZ03QQpbZWkLNnMw44PQ2FLQEeAqZSDDmdlso4t1NcM7knveZ5STexbIIAwJXAbyUdSDFB4FjgJ6l8aTvwZ4pJBCtjpKRbKJLtEelYI+KamTVNq1yPKSPnNZs7gJ7uj3kG2LOXl10aEV/sFucBYPtu5x3W7TER8Y1uj8f19FxETEq7J3Y7/5kycc3MWkV1Uo1XEDAzqyz3bAYgIvYa7DaYmVVJlSYItEyyGQoWLFqYJe6ySXWN1aY880OGZ4oL+Wa0vKY8P7artY/OEhdgcUee2Ivm5vmUR7flq76iYXnucRvf+XCWuI0S7tmYmVlurTLTrAwnGzOzivIwmpmZZdeZaYg9BycbM7OKqk6qcbIxM6ssT302M7PsqjQbLWulznpI2ljS5ZIelPS/kk6V1GvxNUnHSRpTIu6CxrbUzGxwLCFKba2gJZONiqWWfwf8V0RMpiiGNo7la990dxzQb7Kps13uCZpZy4iS/7WClkw2wD7Awog4B5aWKvgMcLSksZK+L2m2pFmSPiXpWIpqmtMlTQeQdEQ6Z46k79YGl/QDSXdKui5V6ETS5pKuknSHpL9I2iod/6WkH6a4y8UxMxtMnSW3VtCqyWZb4I7aAxHxIvAo8BGK8s87RsT2wPkRcRrwOLB3ROwtaUOKxLAPRWmDXSUdlEKNBe6MiJ2A64Gvp+NnAp9KFURPAH5a8/ZbAPtFxPHdG1pbqXPxkpca8b2bmZUSEaW2VtCqw0Ki51l9olgx+oyIWAIQEc/1cN6uwIyIeBpA0vnpdf9FkegvSuf9GvidpHEUK1RfUlOpc2RNvEtS72oFtZU6x43ZtDX+Vc1slVCl2Wit2rO5B9il9oCk8cBEek9Ey52+Eu8VFJ/DCxExpWbbuuYcV+o0s5bTqOJpkiZKmi7pPkn3SPp0Or6mpGvTRK1rJa2RjkvSaZIeSpczdurvPVo12VwHjJH0IQBJbcAPgF9SVNT8aNfFeklrptfUVvS8BXiLpLXTa4+gGDKD4ns+JO2/D7ghDdE9IunQFFOSdsj4/ZmZ1a2TKLWVsAQ4Pv2R/QbgE5K2Ab4AXJcmal2XHgO8HZictqnAz/p7g5ZMNlEMMh4MHCrpQeABYCHwJWAaxbWbWZLupkgYUAxl/VHS9Ih4AvgiMB24m+IazeXpvJeBbSXdQXFN56R0/P3AMSnmPcCBmb9NM7O6NOqaTUQ8ERF3pv2XgPuAjSh+D56bTjsX6Lr2fSBwXhRuBlaXtEFf79Gq12yIiMeAd/Xy9GfTVnv+6cDpNY8vAC7oIW5XBc+vdjv+CLB/D+cftTLtNjNrlrIzzSRNpeiBdDkzXW/u6dxJwI4UI0TrpT/eiYgnJK2bTtsIeKzmZfPSsSd6a0PLJhszM+tb2Xtoaicy9SVNlroUOC4iXqyZMLXCqT02pw8tOYxmZmb9a+A1GyQNp0g050fE79LhJ7uGx9LXp9LxeRQTtrpsTHH7Sa+cbMzMKqojOktt/UmrtpwF3BcRP6x56grgyLR/JHB5zfEPpclUbwDmdw239cbDaA20cMmiLHGXdOYppzuqvdel5uoyctjwLHEBFnYuyRJ3UVueEssj2/L9PdfRNrL/kwYkT9y2jLeEDHs0T/CFL72SJS4smzpbjwYuRfMm4IPAbEkz07EvAd8BLpZ0DMXErEPTc38ADgATub8cAAANmElEQVQeAl4BPtzfGzjZmJlVVKOKp0XEDfR+f+K+PZwfwCdW5j2cbMzMKqo66wc42ZiZVVaVlqtxsjEzqygnGzMzy67MTLNW0ZSpz5JC0g9qHp8g6RvNeO8e2uJKnWY2JLh42opeA94jae0mvV8WrtRpZq2kSvVsmpVsllAslfCZ7k9I2iRVzJyVvr5O0gRJcyUNS+eMkfSYpOH9VNT8WVom+2FJb5F0dloy+5fd3tOVOs2s8hq5gkBuzVxB4CfA+yVN6Hb8xxSrh24PnA+cFhHzKVZrfks6513A1RGxmL4raq5BsZLzZ4ArgVMoqn6+XtKUdE62Sp2dnS57Y2bNU6WeTdOGhdKibucBxwKv1jy1B/CetP8r4D/T/kXAYRRlAg4HflqiouaVERGSZgNPRsRsAEn3AJOAmWSs1Nk+YqPW+Fc1s1VCR+l1nwdfs69B/Ai4Ezinj3O6fmFfAZyciqPtDPyJolfyQkRM6eW1r6WvnTX7XY97+16Xq9TZyznusphZy2nUCgLN0NSFOCPiOeBi4JiawzdR9FygKGB2Qzp3AXArcCrw+4joaFBFTVfqNLMhwbPR+vYDoHZW2rHAhyXNolgI7tM1z10EfIBlw15Qf0VNV+o0syGhM6LU1grUKhePhoJc12zah7XlCMt6Y1fPEnetEeOzxAUYkWn2+RqZVn3eqG1slrgAG0ee1ZkndvRaMKsuOVd93jbTSPeaa+Rb9XnzOVfX/UFvte6upT7V+5+6Lc8/6krwfSNmZhXVKr2WMpxszMwqqkrL1TjZmJlVVKtc/C/DyaaBRrbnqVC5+sg84/4ThueJu0bbmCxxAdqV5/rV2sPyXLPZNNN1FYD1M11b2WBxnmqoOWcjbTBpfpa4YzbMUyW3UcI9GzMzy61VlqIpw8nGzKyiqjSb2MnGzKyi3LMxM7PsOjp9zcbMzDLzbLRuJHUAs4HhFLVtzgV+FIMwlULSgogY1+z3NTNrNF+zWdGrXSsqS1oXuACYwLJaMpUgqT0i8swLNTNbSVW6ZtP0hTgj4ilgKvDJtLpym6TvSbotVev8t65zJX1e0mxJd0v6TjrmSp1mZrh4Wr8i4uFU8nlditWV50fErpJGAjdKugbYCjgI2D0iXkl1baAoVPbRiHhQ0u4UFTX3Sc91Vep8N0WlzjcBHwFukzQlImayrFLn8ZK+RtG7+mQ/cbsqda5wh5ekqRTJkxHD16S9fbWGfU5mZn3xBIFyum5/fhuwvaSuGjMTgMnAfsA5EfEKFLVwWr1S59gxk1rjTwgzWyVUaRhtUJKNpM2ADuApiqTzqYi4uts5+8MKn2R/FTVdqdPMVhmtMkRWRtOv2aRrJGcAP47ik7oa+Jik4en5LSSNBa4BjpY0Jh1f05U6zcyWqVLxtGb1bEZLmsmyqc+/An6YnptGMcR1p4oxrKeBgyLiKklTgNslLQL+AHyJoqLmzyR9JcW7ELh7JdpSW6lzPnBYOl5vXDOzpqrSfTau1NlAua7Z5Fr1ea2ReSpqrpNxkkSuVZ/XzbTq81bkiQte9bnWdpOeyhI356rPa152fd3/gKNHb1Lqd86rr/7dlTrNzGxgOl1iwMzMcqvSyJSTjZlZRVUp2ZS+A9VbYzdgapXiVrHN/iz8WQyVz2IobE2f+mxLTa1Y3JyxqxY3Z+yqxc0Zu2pxc8euNCcbMzPLzsnGzMyyc7IZPGdWLG7O2FWLmzN21eLmjF21uLljV5pv6jQzs+zcszEzs+ycbMzMLDsnGzMzy87JxszMsnOyMTOz7JxszMwsOy/E2SSSNgcOBiZSFJB7EPhNRMxvQOx/AQ4CNqIoc/04cHlEXFVv7F7e72sRcVIdr/8XYGPguoiYW3P86Ig4u464Ag6l+Ax+C+wDHAjcD5wR0bj12CX9KSL2qTPG2hHxTM3jDwC7AXOAX8QA70uQdDBwfUQ8lyrj/gDYEbgXOD4i5tXR5h8Cl0bEjQON0UvcNYFPUvy/exZFocQ9gPuAb0fE83XE3ht4L8v/7E2LiIca0O6m/uxVme+zaQJJxwLvAq4HDgBmAs9TJJ+PR8SMOmL/CNgCOA/o+iWyMfAh4MGI+PTAW97rez4aEa8b4Gu/DbwZuJPiM/lRRJyenrszInaqo10/BdYFRgAvAiOBKyk+8ycH+llImtX9EMVn/jeAiNh+gHGXfr+pQuw/AxcA7wTmRcRnBhj33ojYJu1fBNwMXALsB7w/It46kLgp3tPA34F1gIso/mC6a6DxauL+AZgNjAe2TvsXA28FdoiIAwcY9zvAesB1FEnhEeAB4OMUSeySOtrc9J+9ShvslUBXhY3iB6ct7Y8BZqT91wF31Rn7gV6Oi+J/+IHGfbGX7SVgSZ2fRXvaX52i3Pcp6XG9n8Xs9HU48CwwIj1u73pugHGvAH4NbAVsQlHG/LG0v0kdce+q2b8TGFvT/nra+7ea/Tu6PTezzs/4rvR1MvBV4B6KnuPXgS3qiDszlv1/+49Gtbn2c0z/H9yY9tcA5tT5WWT52Ruqm6/ZNE/XkOVIYDWAiHiU4hdLPRZK2q2H47sCC+uI+wIwOSLGd9tWA56oI257RCwBiIgXKHo34yVdQtEjqUdX3MXAbRGxKD1eAgy4vm9EvBu4lGIpkh2iGPpbHBF/j4i/19He0ZJ2lLQzxR8jL9e0v556xDMknSRpdNo/CJYOJ9U7bBupjQ9GxDcjYlvgX4FRFH84DNQwSWtQDHWNkzQJQNJa1Pf/RWcaogPYEGgDiGJYrt5Sybl+9oYkX7NpjmnAbZJuBvYEvguQxtOfqzP2UcDPJK3Gsq78RIpeyFF1xD2P4i/3J3t47oI64v6vpLdExPUAEdEBHCPpPyjG1evxf5LGRcSCiNi/66Ck9YFF9QSOiMskXQN8U9JHqD8xQpG0f5j2n5O0QUQ8kX7BLqkj7ieBL5OG+YDPSHqZYkjxg3XEhR5+QUfELGAW8MU64p5M0UMCOBqYJimAbYAT64j7beAuSX+j6Jl+DJb+7N1dR1zI97M3JPmaTZNI2pZiLHpORNzf3/kDiL8+xUVKUYz3/1+j36MR0l/bRMSrPTy3UUT8I8N7jqUYonqqQfF2APaIiDMaEa+H+G3AyIh4pQGxJlD0Jp+tv2XQlcwbEauH2G0Uv5OWSGoHplAMqdXTk+6afLAZ8FDqTTdUVX72BpuTzSCR9PGI+GmGuOMoLlo+3MgfrKrFzRnbcfPHrkJcSSMohlMjPd4b2Am4JzwbbQW+ZtMEkj7bbTseOKnrcZ2xf1qz/2aK6a0/AGZLOmBViZsztuPmj121uMltFJNckPQ54FvAaOB4SSfXGXvoGewZCqvCRjGD6yLgaxSzdr5OMfX568DX64x9Z83+dGCntL8ZcPuqEreKba5a3Cq2OfNnMadm/3ZgdNpvB2bVE3sobu7ZNMe2FLNgxgLfi4gTgecj4sS03yjjI+JOgIh4OL3nqhg3Z2zHzR+7KnFflLRd2n+GYkYeFMnGv1u78Wy0JohiivMhkg4ErpV0SgPDb5VuOhQwSdIaEfG8pGHUN626anGr2Oaqxa1im3N+Fh8Fzpd0N/AUcLuk64HtKWbBWQ0nmyaKiMsl/Q/wDZZNlazX1t0ev5y+rkkxbLeqxM0Z23Hzx65aXCJilqSdgLdRTDq4m+Ln+rORYdZb1Xk2mpmZZedxxSaQNC7d0X2PpPmSnpZ0s6SjWjV21eJWsc1Vi1vFNlfxsxiq3LNpAkmXA5cB/0OxtMdY4ELgKxQ3rX2p1WJXLW4V21y1uFVscxU/iyFrsKfDrQobcHe3x7elr8OA+1sxdtXiVrHNVYtbxTZX8bMYqpuH0ZrjZRU3lCHpXaT10KKor1LvYoC5Ylctbs7Yjps/dtXi5o499Ax2tlsVNoqpkLdSrKR8A2kpdoqaIMe2Yuyqxa1im6sWt4ptruJnMVQ3T31ugihWxV1hKfKIeFrSS60Yu2pxc8Z23PyxqxY3d+yhyBMEBpnqqHo5WLGrFjdnbMfNH7tqcXPHrir3bJpAK5YVXvoURcnalotdtbg5Yztu/thVi5s79lDkZNMc6wH/QrH4Zi0BN7Vo7KrFzRnbcfPHrlrc3LGHHCeb5vg9MC4iZnZ/QtKMFo1dtbg5Yztu/thVi5s79pDjazZmZpad77MxM7PsnGzMzCw7JxszM8vOycasRUhqZBVNs5biZGM2AJK+KenTNY+/JelYSZ+TdJukWZJOrHn+vyTdkZajn1pzfEFapv4WYI8mfxtmTeNkYzYwZwFHAqgoMXw48CQwmWIJkynAzpL2TOcfHRE7A7sAx0paKx0fC8yJiN0j4oZmfgNmzeT7bMwGICLmSnpW0o4UN/fdBexKUSL4rnTaOIrk82eKBHNwOj4xHX8W6AAubWbbzQaDk43ZwE0DjgLWB84G9gVOjoif154kaS9gP2CPiHgl3fA3Kj29MCI6mtVgs8HiYTSzgbsM2J+iR3N12o6WNA5A0kaS1gUmAM+nRLMV8IbBarDZYHHPxmyAImKRpOnAC6l3co2krYG/SgJYAHwAuAr4aFq48W/AzYPVZrPB4uVqzAYoTQy4Ezg0Ih4c7PaYtTIPo5kNgKRtgIeA65xozPrnno2ZmWXnno2ZmWXnZGNmZtk52ZiZWXZONmZmlp2TjZmZZff/AV5laAR8C5dmAAAAAElFTkSuQmCC" alt="" width="400" height="273" />
sns.heatmap(df,annot=True,fmt='d')#annot显示是否有字,fmt=‘d’表示显示整数数字
结果:
<matplotlib.axes._subplots.AxesSubplot at 0xb345e10>
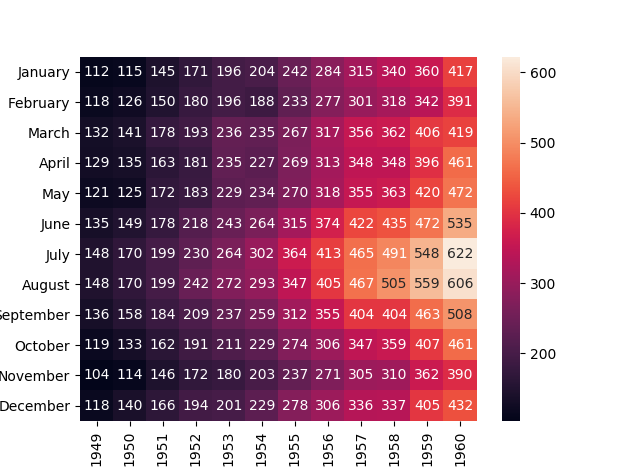
s=df.sum()
print(s)
print(s.index)
print(s.values)
结果:
year
1949 1520
1950 1676
1951 2042
1952 2364
1953 2700
1954 2867
1955 3408
1956 3939
1957 4421
1958 4572
1959 5140
1960 5714
dtype: int64
Int64Index([1949, 1950, 1951, 1952, 1953, 1954, 1955, 1956, 1957, 1958, 1959,
1960],
dtype='int64', name='year')
[1520 1676 2042 2364 2700 2867 3408 3939 4421 4572 5140 5714]
sns.barplot(x=s.index,y=s.values)
结果:
<matplotlib.axes._subplots.AxesSubplot at 0x26009b0>
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYAAAAEKCAYAAAAb7IIBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAFgdJREFUeJzt3X+0ZWV93/H3R0a0YhSECyHDIGQ5CZI2KE4Bl5EYJ4GBmIANLGEZnSrpNAYjrrb+6qoLFUnVtFGpFWUJZjT+IqQEaohkMkoTuxQZFJEf6kwIhSkERgeIlKrBfPvHfq4chnvnnjv3njtDn/drrbPO3s959v7ufc+5+3P2j3NOqgpJUn+esLsXQJK0exgAktQpA0CSOmUASFKnDABJ6pQBIEmdGisAkuyb5LIk30xya5LnJ3lGkg1JNrf7/VrfJLkgyZYkNyY5emQ+a1v/zUnWTmqlJElzG3cP4P3A56rqCOAo4FbgzcDGqloJbGzjACcBK9ttHXAhQJJnAOcCxwLHAOdOh4YkaenNGQBJngYcD1wMUFU/rKr7gVOA9a3beuDUNnwK8LEafBnYN8nBwInAhqraXlX3ARuANYu6NpKksS0bo89PA9uAjyY5CrgeOAc4qKruBqiqu5Mc2PovB+4cmX5ra5ut/VGSrGPYc2CfffZ53hFHHDGvFZKk3l1//fXfqaqpufqNEwDLgKOB362qa5O8n0cO98wkM7TVTtof3VB1EXARwKpVq2rTpk1jLKIkaVqS/zVOv3HOAWwFtlbVtW38MoZAuKcd2qHd3zvSf8XI9IcAd+2kXZK0G8wZAFX1d8CdSX62Na0GbgGuBKav5FkLXNGGrwRe2a4GOg54oB0quho4Icl+7eTvCa1NkrQbjHMICOB3gU8k2Ru4DXgVQ3hcmuQs4A7g9Nb3KuBkYAvwUOtLVW1Pch5wXev3jqravihrIUmat+zJXwftOQBJmr8k11fVqrn6+UlgSeqUASBJnTIAJKlTBoAkdcoAkKROjXsZqCRpEdzz/i9NZL4HnfP8eU/jHoAkdcoAkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkThkAktQpA0CSOmUASFKnDABJ6pQBIEmdMgAkqVMGgCR1ygCQpE4ZAJLUKQNAkjrlj8JL6trt7/u7icz3sNf/5ETmu5jG2gNIcnuSbyS5Icmm1vaMJBuSbG73+7X2JLkgyZYkNyY5emQ+a1v/zUnWTmaVJEnjmM8hoF+qqudU1ao2/mZgY1WtBDa2cYCTgJXttg64EIbAAM4FjgWOAc6dDg1J0tJbyDmAU4D1bXg9cOpI+8dq8GVg3yQHAycCG6pqe1XdB2wA1iygviRpAcYNgAL+Isn1Sda1toOq6m6Adn9ga18O3Dky7dbWNlu7JGk3GPck8Auq6q4kBwIbknxzJ30zQ1vtpP3REw8Bsw7g0EMPHXPxJEnzNdYeQFXd1e7vBS5nOIZ/Tzu0Q7u/t3XfCqwYmfwQ4K6dtO9Y66KqWlVVq6ampua3NpKksc0ZAEn2SfIT08PACcBNwJXA9JU8a4Er2vCVwCvb1UDHAQ+0Q0RXAyck2a+d/D2htUmSdoNxDgEdBFyeZLr/J6vqc0muAy5NchZwB3B6638VcDKwBXgIeBVAVW1Pch5wXev3jqravmhrIkmalzkDoKpuA46aof27wOoZ2gs4e5Z5XQJcMv/FlCQtNr8KQpI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkThkAktQpA0CSOmUASFKn/E1gSXuUP//MdyY275NedsDE5v145B6AJHXKAJCkThkAktQpA0CSOmUASFKnvApI0k697vI7JzbvC166Yu5Omhj3ACSpUwaAJHXKAJCkThkAktQpA0CSOmUASFKnDABJ6pQBIEmdMgAkqVMGgCR1ygCQpE6NHQBJ9krytSSfbeOHJ7k2yeYkn0myd2t/Uhvf0h4/bGQeb2nt30py4mKvjCRpfPPZAzgHuHVk/N3Ae6tqJXAfcFZrPwu4r6qeBby39SPJkcAZwM8Ba4APJtlrYYsvSdpVYwVAkkOAXwU+0sYDvBi4rHVZD5zahk9p47THV7f+pwCfrqofVNXfAluAYxZjJSRJ8zfuHsD7gDcC/9jG9wfur6qH2/hWYHkbXg7cCdAef6D1/3H7DNP8WJJ1STYl2bRt27Z5rIokaT7mDIAkLwHurarrR5tn6FpzPLazaR5pqLqoqlZV1aqpqam5Fk+StIvG+UGYFwC/nuRk4MnA0xj2CPZNsqy9yz8EuKv13wqsALYmWQY8Hdg+0j5tdBpJYzr1so0Tm/efnrZ6YvPWnmfOPYCqektVHVJVhzGcxP18Vb0c+AJwWuu2FriiDV/ZxmmPf76qqrWf0a4SOhxYCXxl0dZEkjQvC/lJyDcBn07yTuBrwMWt/WLg40m2MLzzPwOgqm5OcilwC/AwcHZV/WgB9SVJCzCvAKiqa4Br2vBtzHAVT1V9Hzh9lunPB86f70JKkhafnwSWpE4ZAJLUKQNAkjplAEhSpwwASeqUASBJnTIAJKlTBoAkdcoAkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwv5QRhJzUsu+8RE5vvZ014+kflK4B6AJHXLAJCkThkAktQpA0CSOmUASFKnDABJ6pQBIEmdMgAkqVMGgCR1ygCQpE4ZAJLUqTkDIMmTk3wlydeT3Jzk7a398CTXJtmc5DNJ9m7tT2rjW9rjh43M6y2t/VtJTpzUSkmS5jbOHsAPgBdX1VHAc4A1SY4D3g28t6pWAvcBZ7X+ZwH3VdWzgPe2fiQ5EjgD+DlgDfDBJHst5spIksY3ZwDU4ME2+sR2K+DFwGWtfT1wahs+pY3THl+dJK3901X1g6r6W2ALcMyirIUkad7GOgeQZK8kNwD3AhuAvwHur6qHW5etwPI2vBy4E6A9/gCw/2j7DNOM1lqXZFOSTdu2bZv/GkmSxjJWAFTVj6rqOcAhDO/anz1Tt3afWR6brX3HWhdV1aqqWjU1NTXO4kmSdsG8rgKqqvuBa4DjgH2TTP+gzCHAXW14K7ACoD3+dGD7aPsM00iSltg4VwFNJdm3Df8T4JeBW4EvAKe1bmuBK9rwlW2c9vjnq6pa+xntKqHDgZXAVxZrRSRJ8zPOT0IeDKxvV+w8Abi0qj6b5Bbg00neCXwNuLj1vxj4eJItDO/8zwCoqpuTXArcAjwMnF1VP1rc1ZEkjWvOAKiqG4HnztB+GzNcxVNV3wdOn2Ve5wPnz38xpfn51ct/fyLz/bOXvmEi85V2Bz8JLEmdMgAkqVMGgCR1ygCQpE4ZAJLUqXEuA5UW7FWXr5nIfD/60s9NZL5SD9wDkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkThkAktQpA0CSOuV3AXXqwx8/cSLz/devuHoi85W0+NwDkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkTs0ZAElWJPlCkluT3JzknNb+jCQbkmxu9/u19iS5IMmWJDcmOXpkXmtb/81J1k5utSRJcxlnD+Bh4N9W1bOB44CzkxwJvBnYWFUrgY1tHOAkYGW7rQMuhCEwgHOBY4FjgHOnQ0OStPTm/C6gqrobuLsNfy/JrcBy4BTgRa3beuAa4E2t/WNVVcCXk+yb5ODWd0NVbQdIsgFYA3xqEdfncevqi0+eyHxPPOuqicxX0uPfvM4BJDkMeC5wLXBQC4fpkDiwdVsO3Dky2dbWNlv7jjXWJdmUZNO2bdvms3iSpHkYOwCSPBX4E+D1VfX3O+s6Q1vtpP3RDVUXVdWqqlo1NTU17uJJkuZprABI8kSGjf8nquq/teZ72qEd2v29rX0rsGJk8kOAu3bSLknaDca5CijAxcCtVfUHIw9dCUxfybMWuGKk/ZXtaqDjgAfaIaKrgROS7NdO/p7Q2iRJu8E4PwjzAuAVwDeS3NDa/j3wLuDSJGcBdwCnt8euAk4GtgAPAa8CqKrtSc4Drmv93jF9QliStPTGuQroi8x8/B5g9Qz9Czh7lnldAlwynwWUJE2GnwSWpE4ZAJLUKQNAkjplAEhSpwwASeqUASBJnRrncwBduuOC0yYy30Nfd9lE5itJ8+UegCR1ygCQpE4ZAJLUKQNAkjplAEhSpx43VwFtu/CPJjLfqdf85kTmK0l7OvcAJKlTBoAkdcoAkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkThkAktQpA0CSOmUASFKn5gyAJJckuTfJTSNtz0iyIcnmdr9fa0+SC5JsSXJjkqNHplnb+m9OsnYyqyNJGtc4ewB/CKzZoe3NwMaqWglsbOMAJwEr220dcCEMgQGcCxwLHAOcOx0akqTdY84AqKq/Arbv0HwKsL4NrwdOHWn/WA2+DOyb5GDgRGBDVW2vqvuADTw2VCRJS2hXzwEcVFV3A7T7A1v7cuDOkX5bW9ts7ZKk3WSxTwJnhrbaSftjZ5CsS7IpyaZt27Yt6sJJkh6xqwFwTzu0Q7u/t7VvBVaM9DsEuGsn7Y9RVRdV1aqqWjU1NbWLiydJmsuuBsCVwPSVPGuBK0baX9muBjoOeKAdIroaOCHJfu3k7wmtTZK0myybq0OSTwEvAg5IspXhap53AZcmOQu4Azi9db8KOBnYAjwEvAqgqrYnOQ+4rvV7R1XteGJZkrSE5gyAqjpzlodWz9C3gLNnmc8lwCXzWjpJ0sT4SWBJ6pQBIEmdMgAkqVMGgCR1ygCQpE4ZAJLUKQNAkjplAEhSpwwASeqUASBJnTIAJKlTBoAkdcoAkKROGQCS1CkDQJI6ZQBIUqcMAEnqlAEgSZ0yACSpUwaAJHXKAJCkThkAktQpA0CSOmUASFKnDABJ6pQBIEmdMgAkqVMGgCR1askDIMmaJN9KsiXJm5e6viRpsKQBkGQv4L8CJwFHAmcmOXIpl0GSNFjqPYBjgC1VdVtV/RD4NHDKEi+DJAlIVS1dseQ0YE1V/VYbfwVwbFW9dqTPOmBdG/1Z4Fu7UOoA4DsLXFzrWc96e3Yt683umVU1NVenZbsw44XIDG2PSqCqugi4aEFFkk1VtWoh87Ce9ay3Z9ey3sIt9SGgrcCKkfFDgLuWeBkkSSx9AFwHrExyeJK9gTOAK5d4GSRJLPEhoKp6OMlrgauBvYBLqurmCZRa0CEk61nPeo+LWtZboCU9CSxJ2nP4SWBJ6pQBIEm9qqrHxQ24BLgXuGmk7SjgS8A3gP8OPG2HaQ4FHgT+3UjbOcBNwM3A6xejHnAY8H+BG9rtQyPTPK/13wJcQDvsNqFa5wN3Ag8u1t9ytnrAU4A/A77Z/pbvWoK/5eeAr7d6HwL2mmS9kWmvHJ3XBNfvGobPvUw/duCE6+3NcIz52+15/I0Jvl5+YqTtBoZr29834fU7s/W/sb12DphwvZe1WjcD71msbRnw8+2xm9vjTx532zLXbbdv2MdeUDgeOHqHP9p1wC+24VcD5+0wzZ8Af0wLAOCfMmz8n8JwAvwvgZULrddeFDNuIICvAM9n+AzEnwMnTbDWccDBzB0AC67X/oa/1Ib3Bv56pnVb5PWb/idMe27PmGS99vi/AD45R5/FWr9rgFWL+b8wR723A+9sw09g9g3kov09R6a/Hjh+gq/PZQwb2QPa+HuAt02w3v7AHcBUG18PrF6EessYQuWokTp7teE5ty1zPg/znWB33nb84wN/zyMnslcAt4w8dirw+8DbeCQATgc+MtLnrcAbF1pvJy+Kg4FvjoyfCXx4ErV2mNdOA2Cx67V+7wf+1VLUA57I8C7pZZOsBzwV+CLD91bNtUyLUe8axgiARax3J7DPUtUbmXZlqz3rO9aF1muvkW3AMxk2kB8C1k2w3j8H/nJk/BXABxeh3snAH80w/djblp3dHu/nAG4Cfr0Nn077kFmSfYA3MbzD2bH/8Un2T/IUhj/uCsY3Y73m8CRfS/I/krywtS1n+PDbtK2tbRK1FmqX6yXZF/g1YOOk6yW5muGd3feAyyZc7zzgPwMPzaPOQuoBfDTJDUnemmSmT84vSr32nAGcl+SrSf44yUGTqreDM4HPVNtyTaJeVf0D8BqGQyR3MYT4xZOqx3AY5ogkhyVZxvAGdDG2LT8DVJKr2/P0xta+kG3Ljz3eA+DVwNlJrmc4xvjD1v524L1V9eBo56q6FXg3sIFHjic/vAj17gYOrarnAv8G+GSSpzHGV18sYq2F2qV67cX+KeCCqrpt0vWq6kSGdz9PAl48qXpJngM8q6oun0eNha7fy6vqnwEvbLdXTLDeMoZP4v/Pqjqa4Rjzf5rw+k07g+E1Mx/zff6eyBAAzwV+iuEwylsmVa+q7mv1PsNwOPR2Fmfbsgz4BeDl7f6lSVazsG3LyBTz3GXYnTd2vjv7M8BX2vD0E3A7cD+wHXjtDNP8HvA7C603w2PXAKtYwCGg+dbaoW3eh4B2tR7DCa0LlqreSPta4AMTfO5ew/DO8XaGd1c/BK5ZwvX7lxNevwD/B3hCa18B3LwEr5ejgG9P+vXCcEhm40j78cBVS/j8rWPnJ4LHqscQln848thbgTfgISBIcmC7fwLwHxiO81FVL6yqw6rqMOB9wO9V1Qd2mOZQhhN8Y78Tma1ekqkMv3VAkp9mOMZ5W1XdDXwvyXFtd/6VwBWTqDXuOixmvSTvBJ4OvH7S9ZI8NcnBrX0Zw+G7b06qXlVdWFU/1V5Dv8Cw0XrRBNdvWZIDWvsTgZcwHBaY1PoVw3mU6XVaDdwyqXojk57J/N/970q9/w0cmWT6GzF/Bbh1kus3Ms1+wO8AH1loPYZvTfj5JE9pr/tfZDg/sMvblkeZb2LsrhvDi+Zu4B8Y3pGdxXBJ57fb7V3MfInl23j0ZaB/zfBC/zqznKWfbz3gNxgu0fo68FXg10bms4rhH/lvgA/MsoyLVes9bfp/bPdvm9S6MRw+KIZ/qulL4n5rgvUOYrhSYvoyu/8CLJvkczfOu7VFXL99GK6MmV6/9zP7Za6L9Xp5JvBXreZGhkMbE/17Mmwsj1is//U51u+3GV6fNzKE3f4Trvcphm3LLcxyhdqubMuA32w1b2Jkr4Ixti1z3fwqCEnq1OP6EJAkadcZAJLUKQNAkjplAEhSpwwASeqUASBJnTIApAmb/uCQtKcxAKQRSc5Lcs7I+PlJXpfkDUmuS3JjkrePPP6nSa5PcnOSdSPtDyZ5R5JrGb6yV9rjGADSo13M8D1D0x/LPwO4h+Ej/8cAzwGel+T41v/VVfU8hk9lvi7J/q19H4ZPDx9bVV9cyhWQxrVsdy+AtCepqtuTfDfJcxm+fuJrDF8sdkIbhuF3AlYyfI3C65K8tLWvaO3fBX7E8KM10h7LAJAe6yMM38b5kwzfdroa+I9V9eHRTkleBPwy8PyqeijJNcCT28Pfr6ofLdUCS7vCQ0DSY10OrGF45391u706yVMBkixv3974dOC+tvE/guEnOaXHDfcApB1U1Q+TfAG4v72L/4skzwa+NHzzLg8yfEPj54DfTnIjw4+5f3l3LbO0K/w2UGkH7eTvV4HTq2rz7l4eaVI8BCSNSHIkw++7bnTjr//fuQcgSZ1yD0CSOmUASFKnDABJ6pQBIEmdMgAkqVP/D6JozQGJBrDbAAAAAElFTkSuQmCC" alt="" />
print(type(s))
s.plot(kind='bar')#复习matplotlib画出柱状图
结果:
<matplotlib.axes._subplots.AxesSubplot at 0xbce8f98>
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYAAAAEaCAYAAAAYOoCaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAF1RJREFUeJzt3X20XXV95/H3RyLqgEjQgDSgaJsWcCqIKeDSOggWItqCa2SGrlaj0pXliNWpTqfodBoFH3DNqlhnVR0GmIGOiqjjkLEsMY1gx05BwlN4biIqRBCiCfjA+BD8zh/7d+EQbnLPvTnnXnL3+7XWWWfv3/7t8/3tSzifsx/OPqkqJEn986S5HoAkaW4YAJLUUwaAJPWUASBJPWUASFJPGQCS1FNDBUCSvZN8PsntSW5L8pIk+yRZnWR9e17Y+ibJx5JsSLIuyREDr7O89V+fZPm4NkqSNLVh9wD+CvhyVR0MHAbcBpwBrKmqJcCaNg/wKmBJe6wAPgGQZB9gJXAUcCSwciI0JEmzb8oASLIX8HLgfICq+nlVPQCcBFzYul0InNymTwIuqs5VwN5J9gdOAFZX1eaq2gKsBpaNdGskSUMbZg/g+cAm4L8luT7JeUn2AParqnsB2vO+rf9i4O6B9Te2tu21S5LmwIIh+xwB/HFVXZ3kr3j0cM9kMklb7aD9sSsnK+gOHbHHHnu8+OCDDx5iiJKkCddee+33q2rRVP2GCYCNwMaqurrNf54uAO5Lsn9V3dsO8dw/0P/AgfUPAO5p7cds037ltsWq6lzgXIClS5fW2rVrhxiiJGlCku8M02/KQ0BV9T3g7iS/0ZqOA24FVgETV/IsBy5t06uAN7SrgY4GHmyHiC4Hjk+ysJ38Pb61SZLmwDB7AAB/DHwqye7AncCb6MLjkiSnAXcBp7S+lwEnAhuAh1pfqmpzkrOAa1q/M6tq80i2QpI0bXki3w7aQ0CSNH1Jrq2qpVP185vAktRTBoAk9ZQBIEk9ZQBIUk8ZAJLUU8NeBipJGoODzvjbGa337bNfvdO13QOQpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKH4WXpAFz+SPts22oPYAk305yU5IbkqxtbfskWZ1kfXte2NqT5GNJNiRZl+SIgddZ3vqvT7J8PJskSRrGdA4BvaKqDq+qpW3+DGBNVS0B1rR5gFcBS9pjBfAJ6AIDWAkcBRwJrJwIDUnS7NuZcwAnARe26QuBkwfaL6rOVcDeSfYHTgBWV9XmqtoCrAaW7UR9SdJOGDYACvhKkmuTrGht+1XVvQDted/Wvhi4e2Ddja1te+2SpDkw7Engl1bVPUn2BVYnuX0HfTNJW+2g/bErdwGzAuA5z3nOkMOTJE3XUHsAVXVPe74f+CLdMfz72qEd2vP9rftG4MCB1Q8A7tlB+7a1zq2qpVW1dNGiRdPbGknS0KYMgCR7JHn6xDRwPHAzsAqYuJJnOXBpm14FvKFdDXQ08GA7RHQ5cHyShe3k7/GtTZI0B4Y5BLQf8MUkE/0/XVVfTnINcEmS04C7gFNa/8uAE4ENwEPAmwCqanOSs4BrWr8zq2rzyLZEkjQtUwZAVd0JHDZJ+w+A4yZpL+D07bzWBcAF0x+mJGnUvBWEJPWUASBJPWUASFJPGQCS1FMGgCT1lAEgST1lAEhSTxkAktRTBoAk9ZQBIEk9ZQBIUk/5o/CSntCefcUNM1rve684fMQjmX/cA5CknjIAJKmnDABJ6ikDQJJ6ypPAkqZtzVd/ddrrHHfsN8cwEu0M9wAkqacMAEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSemroAEiyW5Lrk3ypzT8vydVJ1if5bJLdW/tT2vyGtvyggdd4d2u/I8kJo94YSdLwprMH8A7gtoH5DwPnVNUSYAtwWms/DdhSVb8GnNP6keRQ4FTgBcAy4ONJdtu54UuSZmqoAEhyAPBq4Lw2H+BY4POty4XAyW36pDZPW35c638ScHFV/ayqvgVsAI4cxUZIkqZv2D2AjwL/Hvhlm38m8EBVbW3zG4HFbXoxcDdAW/5g6/9I+yTrPCLJiiRrk6zdtGnTNDZFkjQdUwZAktcA91fVtYPNk3StKZbtaJ1HG6rOraqlVbV00aJFUw1PkjRDw/wgzEuB30tyIvBUYC+6PYK9kyxon/IPAO5p/TcCBwIbkywAngFsHmifMLiOJGmWTRkAVfVu4N0ASY4B/l1V/UGSzwGvAy4GlgOXtlVWtfl/bMu/WlWVZBXw6SQfAX4FWAJ8Y7SbI/XTe9/73lldT/PDzvwk5J8BFyd5P3A9cH5rPx/4myQb6D75nwpQVbckuQS4FdgKnF5VD+9EfUnSTphWAFTVlcCVbfpOJrmKp6p+CpyynfU/AHxguoOUJI2e3wSWpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSempnfhFM0nZsPOP/zGi9A87+7RGPRNo+9wAkqacMAEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeqpKQMgyVOTfCPJjUluSfK+1v68JFcnWZ/ks0l2b+1PafMb2vKDBl7r3a39jiQnjGujJElTG2YP4GfAsVV1GHA4sCzJ0cCHgXOqagmwBTit9T8N2FJVvwac0/qR5FDgVOAFwDLg40l2G+XGSJKGN2UAVOfHbfbJ7VHAscDnW/uFwMlt+qQ2T1t+XJK09our6mdV9S1gA3DkSLZCkjRtQ50DSLJbkhuA+4HVwDeBB6pqa+uyEVjcphcDdwO05Q8Czxxsn2QdSdIsGyoAqurhqjocOIDuU/shk3Vrz9nOsu21P0aSFUnWJlm7adOmYYYnSZqBaV0FVFUPAFcCRwN7J5n4PYEDgHva9EbgQIC2/BnA5sH2SdYZrHFuVS2tqqWLFi2azvAkSdMwzFVAi5Ls3aafBrwSuA24Anhd67YcuLRNr2rztOVfrapq7ae2q4SeBywBvjGqDZEkTc8wvwi2P3Bhu2LnScAlVfWlJLcCFyd5P3A9cH7rfz7wN0k20H3yPxWgqm5JcglwK7AVOL2qHh7t5kiShjVlAFTVOuBFk7TfySRX8VTVT4FTtvNaHwA+MP1hSjvnL//1a2a03rs++6URj0R64vCbwJLUUwaAJPWUASBJPWUASFJPGQCS1FPDXAYqjdxfv+WrM1rv9E8eO+KRSP3lHoAk9ZQBIEk9ZQBIUk8ZAJLUUwaAJPWUASBJPWUASFJPGQCS1FMGgCT1lAEgST1lAEhSTxkAktRT3gxOANx28CEzWu+Q228b8UgkzRb3ACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknpoyAJIcmOSKJLcluSXJO1r7PklWJ1nfnhe29iT5WJINSdYlOWLgtZa3/uuTLB/fZkmSpjLMHsBW4F1VdQhwNHB6kkOBM4A1VbUEWNPmAV4FLGmPFcAnoAsMYCVwFHAksHIiNCRJs2/KW0FU1b3AvW36R0luAxYDJwHHtG4XAlcCf9baL6qqAq5KsneS/Vvf1VW1GSDJamAZ8JkRbs+88ZsX/uaM1rtp+U0jHomk+Wpa5wCSHAS8CLga2K+Fw0RI7Nu6LQbuHlhtY2vbXrskaQ4MHQBJ9gS+APzbqvrhjrpO0lY7aN+2zooka5Os3bRp07DDkyRN01ABkOTJdG/+n6qq/9ma72uHdmjP97f2jcCBA6sfANyzg/bHqKpzq2ppVS1dtGjRdLZFkjQNw1wFFOB84Laq+sjAolXAxJU8y4FLB9rf0K4GOhp4sB0iuhw4PsnCdvL3+NYmSZoDw/wewEuB1wM3Jbmhtb0HOBu4JMlpwF3AKW3ZZcCJwAbgIeBNAFW1OclZwDWt35kTJ4QlSbNvmKuAvs7kx+8BjpukfwGnb+e1LgAumM4AJUnj4TeBJamnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSemqYL4IJ4L3PmOF6D452HJI0Iu4BSFJPGQCS1FMGgCT1lAEgST21y54EPuiMv53Ret8++9UjHokk7ZrcA5CknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknjIAJKmnpgyAJBckuT/JzQNt+yRZnWR9e17Y2pPkY0k2JFmX5IiBdZa3/uuTLB/P5kiShjXMHsB/B5Zt03YGsKaqlgBr2jzAq4Al7bEC+AR0gQGsBI4CjgRWToSGJGluTBkAVfX3wOZtmk8CLmzTFwInD7RfVJ2rgL2T7A+cAKyuqs1VtQVYzeNDRZI0i2Z6DmC/qroXoD3v29oXA3cP9NvY2rbXLkmaI6M+CZxJ2moH7Y9/gWRFkrVJ1m7atGmkg5MkPWqmAXBfO7RDe76/tW8EDhzodwBwzw7aH6eqzq2qpVW1dNGiRTMcniRpKjMNgFXAxJU8y4FLB9rf0K4GOhp4sB0iuhw4PsnCdvL3+NYmSZojC6bqkOQzwDHAs5JspLua52zgkiSnAXcBp7TulwEnAhuAh4A3AVTV5iRnAde0fmdW1bYnliVJs2jKAKiq39/OouMm6VvA6dt5nQuAC6Y1OknS2PhNYEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknjIAJKmnDABJ6ikDQJJ6ygCQpJ4yACSppwwASeopA0CSesoAkKSeMgAkqacMAEnqKQNAknrKAJCknjIAJKmnZj0AkixLckeSDUnOmO36kqTOrAZAkt2AvwZeBRwK/H6SQ2dzDJKkzmzvARwJbKiqO6vq58DFwEmzPAZJEpCqmr1iyeuAZVX1R23+9cBRVfW2gT4rgBVt9jeAO2ZQ6lnA93dyuNaznvWe2LWst33PrapFU3VaMIMX3hmZpO0xCVRV5wLn7lSRZG1VLd2Z17Ce9az3xK5lvZ0324eANgIHDswfANwzy2OQJDH7AXANsCTJ85LsDpwKrJrlMUiSmOVDQFW1NcnbgMuB3YALquqWMZTaqUNI1rOe9XaJWtbbSbN6EliS9MThN4ElqacMAEnqKQNAknrKAJCknjIAJKmnZvubwGOR5FeB19J9yWwrsB74TFU9OKZ6JwAnA4vpvsl8D3BpVX15HPV2MI6/qKozx/C6J9B9SW9NVX17oP3NVXXBiGsFOIXu7/h54Fi6+0PdDnyyqn45ynrbGcNXq+rYMb32s6rq+wPzf0h3T6ybgf9aI74ML8lrga9V1eYki4C/BF4E3Aq8q6o2jrjeR4AvVNU/jPJ1t1NrH+BtdP+/nQ+8B3gJcBvwwaraMoaarwD+JY99bzmvqjaMularN6vvLbv8ZaBJ3g78LvA14ETgBmALXSC8taquHHG9jwK/DlxE981m6N4s3wCsr6p3jLLeFGO5q6qeM+LX/CDwMuA6ur/rR6vqP7dl11XVESOu93FgX2B34IfAU4D/Tfff8r5R/z2TrNu2ie6/5x0AVfXCEdd75G+W5M+B3wY+DbwG2FhVfzLierdW1aFt+rPAVcDngFcCf1BVvzPiepuA7wCLgM/SffC6fpQ1BmpdBtwE7AUc0qYvAX4HOKyqRnpjySRnA/sBa+jelL8F/BPwVrrA+dyI683+e0tV7dIPun8Eu7XpfwZc2aafA1w/hnr/tJ32tP9Io673w+08fgRsHdPfc0Gb3hu4DDinzY/j73lTe34y8ANg9za/YGLZiOutAv4HcDDwXOAg4O42/dwx1Lt+YPo6YI+B7R3H9t0xMH3tNstuGNf2AUuA/wjcQrf3thL49RHXuqE9B/juLGzbTQPTC4B/aNMLgZvHUG9W31uqat6cA5g4lPUU4OkAVXUX3f9ko/bTJEdO0v5bwE/HUO8BYElV7bXN4+nAvWOot6CqtgJU1QN0ewF7Jfkc3af0UZuo9QvgmupuE04bw8OjLlZVvwd8ge4blodVd4jrF1X1nar6zqjrAU9L8qIkL6b7oPKTNo5fMIbtA65McmaSp7Xpk+GRQxnjOCRaAFW1vqrOqqoXAP8KeCrdh4dRelKShXSHY/ZMchBAkmcynn+bv2yHnQB+he7uBVR3qGmyG1vurNl+b5kX5wDOA65JchXwcuDDAO345+Yx1Hsj8IkkT+fR3bQD6T6Vv3EM9S6i+3R63yTLPj2Get9M8i+q6msAVfUwcFqS99MdCx217yXZs6p+XFXLJhqTPBv4+RjqUVVfTPIV4Kwkf8R43jwm3At8pE1vTrJ/Vd3b3rS2jqHe24D/wKO3Uf+TJD+hO6z2+jHUe9wbYVWtA9YB7x5xrQ/R7V0AvBk4L0nR/bjU+0ZcC+CDwPVJ7qDbY/w38Mh7y41jqPdGZve9Zdc/BwCQ5AV0xwRvrqrbp+o/oprPpjtRE7pjud+bjbrj1j45UlX/b5Jli6vqu7M0jj3oDpfcP+Y6hwEvqapPjrPOJHV3A55SVQ+NscYz6PbofjDGGntW1Y/H9fqT1NuN7n1ra5IFwOF0h4PGsTc8ceL5+XQ/ZPXAOGpMUnPW3lvmRQBsK8lbq+rjs1RrT7oTN3fOxj8Q61nPerNfazbqtTsk/6ImDvx3h+2OAG6pcV1hOI4TC7P5AN65zeNddL+g807gnWOo9/GB6ZcBdwFX0J1IPNF61rPeeOrN521rNW4EFrbpPwX+L/DnwGrgQ6OuV1XzIgB+RHf52V/QXXmwku4y0JXAyjHUu25g+grgiDb9fGCt9axnvfHUm8/b1l735oHptcDT2vQCYN2o61XNj6uAXkB3dn4P4D9V1fuALVX1vjY9TntV1XUAVXVnG4f1rGe98debj9v2wyT/vE1/n+5KKugCYCzv1bv8VUDVXe75uiQnAauTnDPmkge3LxMFOCjJwqrakuRJjOeyU+tZz3qzX2su6r0F+FSSG4H7gbVJvga8kO6KpJHb5QNgQlVdmuTvgPfy6CVU43DINvM/ac/70B2Gsp71rDeeevN526iqdUmOAI6nO9l8I9172TtrTCe55+VVQJKkqe3y5wCS7Nm++XhLkgeTbEpyVZI3Ws961ps/9ebzts1FPZgHewBJLgW+CPwd3VfQ9wAuprt86rtV9R7rWc96u369+bxtc1EPmBeXgd64zfw17flJwO3Ws5715ke9+bxtc1Gvan5cBvqTJC8DSPK7tPv/VHcf+XHcsMl61rPe3NSbz9s2F/XmxR7AC4Fv0N018+u0W9DS3Z/87daznvXmR735vG1zUa+qdv3LQKu78+DjbqFaVZuS/Mh61rPe/Kg3n7dtLurBPDgJvCMZwy9mWc961nvi1ZvP2zbOerv8HkAe/xN/jyyi+zk361nPevOg3nzetrmoB/MgAOj+MCfQ3QBuUOjupmc961lvftSbz9s2F/XmRQB8Cdizqm7YdkGSK61nPevNm3rzedvmot78PgcgSdq++fA9AEnSDBgAktRTBoAk9ZQBII1ZknH/WpU0IwaANCDJWUneMTD/gSRvT/KnSa5Jsi7J+waW/68k17Zb+K4YaP9xu7Xv1cBLZnkzpKEYANJjnQ8sB0j303+nAvcBS+i+pn848OIkL2/931xVLwaWAm9P8szWvgfdj3wfVVVfn80NkIY1H74HII1MVX07yQ+SvIjuiznXA79F9zN917due9IFwt/Tvem/trUf2Np/ADwMfGE2xy5NlwEgPd55wBuBZwMXAMcBH6qq/zLYKckxwCuBl1TVQ+3LOk9ti39aVQ/P1oClmfAQkPR4XwSW0X3yv7w93pxkT4Aki5PsCzwD2NLe/A8Gjp6rAUsz4R6AtI2q+nmSK4AH2qf4ryQ5BPjHJAA/Bv4Q+DLwlnYTrzuAq+ZqzNJMeCsIaRvt5O91wClVtX6uxyONi4eApAFJDgU2AGt889d85x6AJPWUewCS1FMGgCT1lAEgST1lAEhSTxkAktRTBoAk9dT/BzJUEqW4Q+T4AAAAAElFTkSuQmCC" alt="" />
seaborn设置图形显示效果
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
x=np.linspace(0,14,100)#等差数列,在0,14之间等分为100份
y1=np.sin(x)
y2=np.sin(x+2)*1.25
def sinplot():
plt.plot(x,y1)
plt.plot(x,y2)
结果:
import seaborn as sns
sinplot()#seaborn为其定义了5种风格,下图为默认风格
style=['darkgrid','dark','white','whitegrid','ticks']
结果:
sns.set_style(style[3])
sinplot()
sns.axes_style()#显示出主题的参数设置,可更改,见下条程序
结果:
{'axes.axisbelow': True,
'axes.edgecolor': '.8',
'axes.facecolor': 'white',
'axes.grid': True,
'axes.labelcolor': '.15',
'axes.linewidth': 1.0,
'figure.facecolor': 'white',
'font.family': ['sans-serif'],
'font.sans-serif': ['Arial',
'DejaVu Sans',
'Liberation Sans',
'Bitstream Vera Sans',
'sans-serif'],
'grid.color': '.8',
'grid.linestyle': '-',
'image.cmap': 'rocket',
'legend.frameon': False,
'legend.numpoints': 1,
'legend.scatterpoints': 1,
'lines.solid_capstyle': 'round',
'text.color': '.15',
'xtick.color': '.15',
'xtick.direction': 'out',
'xtick.major.size': 0.0,
'xtick.minor.size': 0.0,
'ytick.color': '.15',
'ytick.direction': 'out',
'ytick.major.size': 0.0,
'ytick.minor.size': 0.0}
sns.set_style(style[3],{'axes.facecolor':'red'})
sinplot()
结果:
{'axes.axisbelow': True,
'axes.edgecolor': '.8',
'axes.facecolor': 'red',
'axes.grid': True,
'axes.labelcolor': '.15',
'axes.linewidth': 1.0,
'figure.facecolor': 'white',
'font.family': ['sans-serif'],
'font.sans-serif': ['Arial',
'DejaVu Sans',
'Liberation Sans',
'Bitstream Vera Sans',
'sans-serif'],
'grid.color': '.8',
'grid.linestyle': '-',
'image.cmap': 'rocket',
'legend.frameon': False,
'legend.numpoints': 1,
'legend.scatterpoints': 1,
'lines.solid_capstyle': 'round',
'text.color': '.15',
'xtick.color': '.15',
'xtick.direction': 'out',
'xtick.major.size': 0.0,
'xtick.minor.size': 0.0,
'ytick.color': '.15',
'ytick.direction': 'out',
'ytick.major.size': 0.0,
'ytick.minor.size': 0.0}
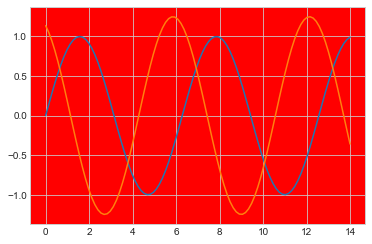
sinplot()#原本的设置已经改变 ,要想恢复到以前的形式,需要清空当前风格设置
结果:
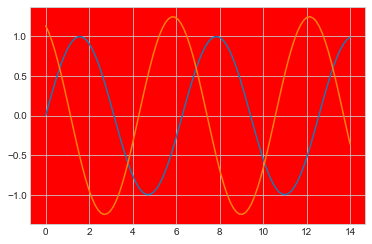
sns.set()#清空当前风格设置
sinplot()#回到默认设置
结果:
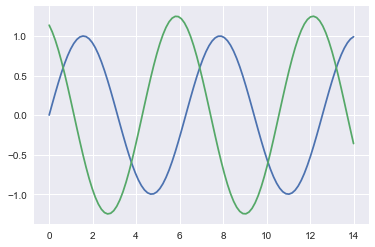
context=['paper','notebook','talk','poster']#曲线属性
sns.set_context(context[0])
sinplot()
结果:
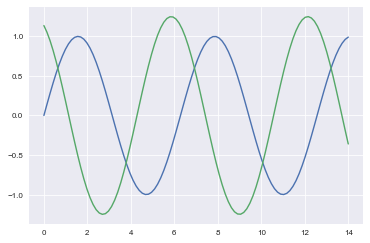
sns.set_context(context[3])#与第0个相比会变粗,变大
sinplot()
sns.plotting_context()#显示出属性的设置
结果:
{'axes.labelsize': 17.6,
'axes.titlesize': 19.200000000000003,
'font.size': 19.200000000000003,
'grid.linewidth': 1.6,
'legend.fontsize': 16.0,
'lines.linewidth': 2.8000000000000003,
'lines.markeredgewidth': 0.0,
'lines.markersize': 11.200000000000001,
'patch.linewidth': 0.48,
'xtick.labelsize': 16.0,
'xtick.major.pad': 11.200000000000001,
'xtick.major.width': 1.6,
'xtick.minor.width': 0.8,
'ytick.labelsize': 16.0,
'ytick.major.pad': 11.200000000000001,
'ytick.major.width': 1.6,
'ytick.minor.width': 0.8}
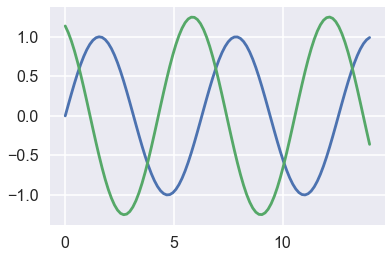
sns.set_context(context[3],rc={'grid.linewidth': 10})#sns.set_context(context=None, font_scale=1, rc=None)
sinplot()
结果:
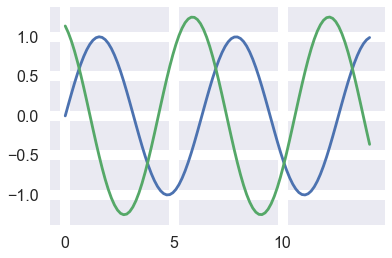
sinplot()#原本的设置已经改变 ,要想恢复到以前的形式,需要清空当前风格设置
结果:
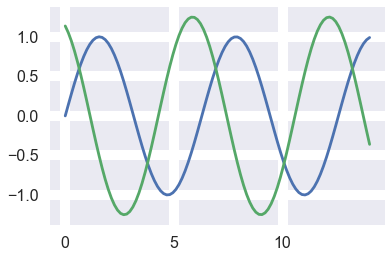
sns.set()#清空当前风格设置
sinplot()#回到默认设置
结果:
seaborn强大的调色功能
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
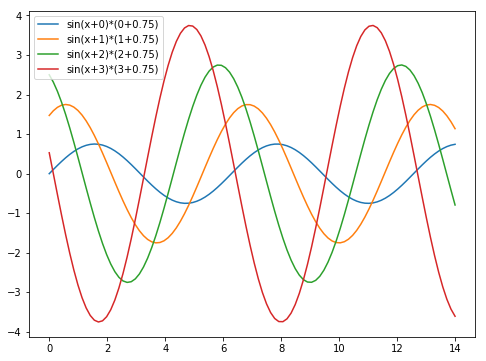
def sinplot():
x=np.linspace(0,14,100)
plt.figure(figsize=(8,6))#调整图像大小
for i in range(4):
plt.plot(x,np.sin(x+i)*(i+0.75),label='sin(x+%s)*(%s+0.75)'%(i,i))
plt.legend()
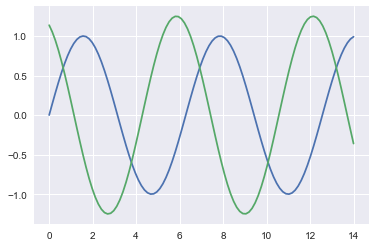
sinplot()
结果:
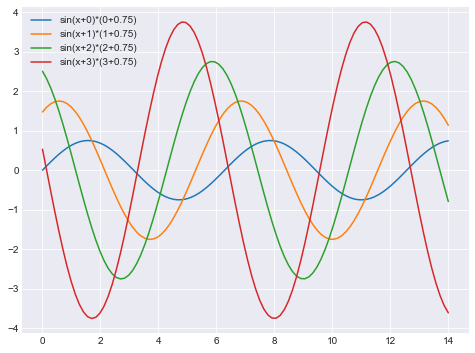
import seaborn as sns
sinplot()
结果:
sns.color_palette()#当前系统所使用的调色板 每组中有三个值,分别为RGB
结果:
[(0.12156862745098039, 0.4666666666666667, 0.7058823529411765),
(1.0, 0.4980392156862745, 0.054901960784313725),
(0.17254901960784313, 0.6274509803921569, 0.17254901960784313),
(0.8392156862745098, 0.15294117647058825, 0.1568627450980392),
(0.5803921568627451, 0.403921568627451, 0.7411764705882353),
(0.5490196078431373, 0.33725490196078434, 0.29411764705882354),
(0.8901960784313725, 0.4666666666666667, 0.7607843137254902),
(0.4980392156862745, 0.4980392156862745, 0.4980392156862745),
(0.7372549019607844, 0.7411764705882353, 0.13333333333333333),
(0.09019607843137255, 0.7450980392156863, 0.8117647058823529)]
sns.palplot(sns.color_palette())#画出色板的颜色
结果:

pal_style=['deep','muted','pastel','bright','dark','colorblind']#6种主题分类色板
sns.palplot(sns.color_palette('deep'))
结果:

sns.set_palette(sns.color_palette('dark'))#设置为dark色板
sinplot()
结果:
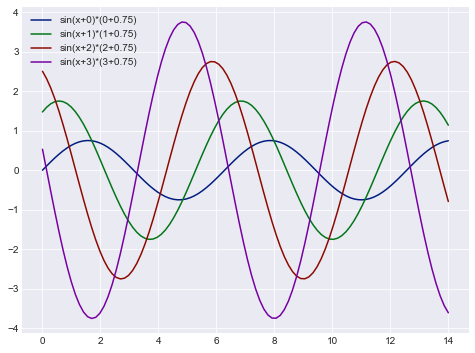
sns.set()#恢复到以前默认的色板
sinplot()
结果:
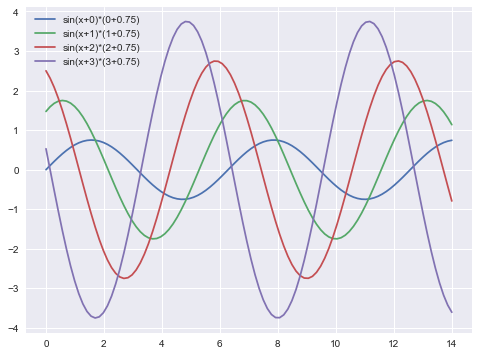
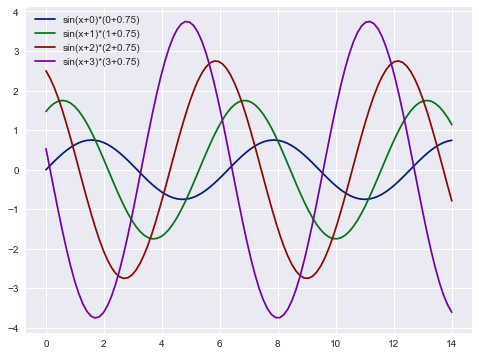
with sns.color_palette('dark'):#设置临时色板
sinplot()
结果:
结果:
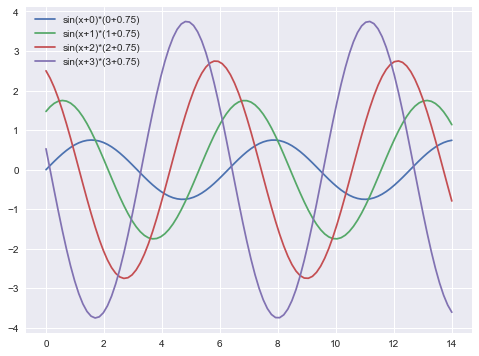
pall=sns.color_palette([(0.5,0.1,0.7),(0.3,0.1,0.9)])#生成自己的色板
sns.palplot(pall)
结果:

sns.palplot(sns.color_palette('hls',8))#生成8种颜色的色板,随便指定数目
结果:























