网络流 P3358 最长k可重区间集问题

P3358 最长k可重区间集问题

题目描述

对于给定的开区间集合 I 和正整数 k，计算开区间集合 I 的最长 k可重区间集的长度。

输入输出格式

输入格式：

的第 1 行有 2 个正整数 n和 k，分别表示开区间的个数和开区间的可重迭数。接下来的 n行，每行有 2 个整数，表示开区间的左右端点坐标。

输出格式：

将计算出的最长 k可重区间集的长度输出

输入输出样例

输入样例#1： 复制

4 2
1 7
6 8
7 10
9 13 

输出样例#1： 复制

15

说明

对于100%的数据，1\le n\le 5001≤n≤500,1\le k\le 31≤k≤3

写一下这个题目的思路，这个图很难建。
看了一下题解，觉得很巧妙。

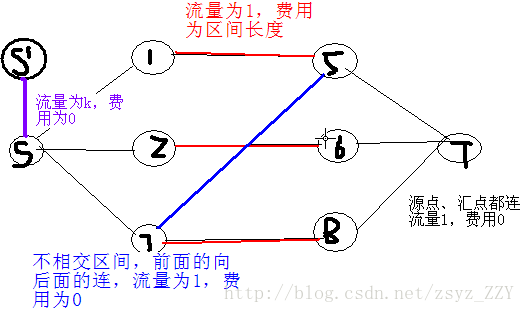
看了这个图就好理解一点了，就是你要把k假定为网络流的最大流量，把每一个区间离散化。

这个看代码更好理解一些，不过可以抽象的讲一下。

就是你把这些区间互不相重叠的划成一条路，假设有5条路，k=2，

那么最多只能从这五条路里面选择两条路，因为如果大于等于2，那么就会出现问题，比如说，第一个区间和第二个区间，

则第二个区间里的每一段，如果不是和第一个区间肯定都是和第一个区间的某一段有交集。

。。。。不好说，还是看代码吧，多搜搜题解，不放弃，最后总会写的。

#include <cstdio>
#include <cstdlib>
#include <queue>
#include <vector>
#include <iostream>
#include <algorithm>
#include <map>
#include <cstring>
#include <string>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 1e5;
struct edge
{
    int u, v, c, f, cost;
    edge(int u, int v, int c, int f, int cost) :u(u), v(v), c(c), f(f), cost(cost) {}
};
vector<edge>e;
vector<int>G[maxn];
int a[maxn];//找增广路每个点的水流量
int p[maxn];//每次找增广路反向记录路径
int d[maxn];//SPFA算法的最短路
int inq[maxn];//SPFA算法是否在队列中
int s, t;
void init(int n)
{
    for (int i = ; i <= n; i++)G[i].clear();
    e.clear();
}
void add(int u, int v, int c, int cost)
{
    e.push_back(edge(u, v, c, , cost));
    e.push_back(edge(v, u, , , -cost));
    int m = e.size();
    G[u].push_back(m - );
    G[v].push_back(m - );
}
bool bellman(int s, int t, int& flow, long long & cost)
{
    memset(d, 0xef, sizeof(d));
    memset(inq, , sizeof(inq));
    d[s] = ; inq[s] = ;//源点s的距离设为0，标记入队
    p[s] = ; a[s] = INF;//源点流量为INF（和之前的最大流算法是一样的）

    queue<int>q;//Bellman算法和增广路算法同步进行，沿着最短路拓展增广路，得出的解一定是最小费用最大流
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        inq[u] = ;//入队列标记删除
        for (int i = ; i < G[u].size(); i++)
        {
            edge & now = e[G[u][i]];
            int v = now.v;
            if (now.c > now.f && d[v] < d[u] + now.cost)
                //now.c > now.f表示这条路还未流满（和最大流一样）
                //d[v] > d[u] + e.cost Bellman 算法中边的松弛
            {
                d[v] = d[u] + now.cost;//Bellman 算法边的松弛
                p[v] = G[u][i];//反向记录边的编号
                a[v] = min(a[u], now.c - now.f);//到达v点的水量取决于边剩余的容量和u点的水量
                if (!inq[v]) { q.push(v); inq[v] = ; }//Bellman 算法入队
            }
        }
    }
    if (d[t] < )return false;//找不到增广路
    flow += a[t];//最大流的值，此函数引用flow这个值，最后可以直接求出flow
    cost += (long long)d[t] * (long long)a[t];//距离乘上到达汇点的流量就是费用
    for (int u = t; u != s; u = e[p[u]].u)//逆向存边
    {
        e[p[u]].f += a[t];//正向边加上流量
        e[p[u] ^ ].f -= a[t];//反向边减去流量 （和增广路算法一样）
    }
    return true;
}
int MaxcostMaxflow(int s, int t, long long & cost)
{
    cost = ;
    int flow = ;
    while (bellman(s, t, flow, cost));//由于Bellman函数用的是引用，所以只要一直调用就可以求出flow和cost
    return flow;//返回最大流，cost引用可以直接返回最小费用
}

struct node
{
    int l, r;
}exa[maxn];
bool cmp(node a,node b)
{
    return a.l < b.l;
}
int main()
{
    int n, m;
    cin >> n >> m;
    int s1 = ;
    s = , t =  * n + ;
    for(int i=;i<=n;i++)
    {
        cin >> exa[i].l >> exa[i].r;
        if (exa[i].l > exa[i].r) swap(exa[i].l, exa[i].r);
    }
    sort(exa + , exa +  + n, cmp);
    add(s, s1, m, );
    for(int i=;i<=n;i++)
    {
        add(s1,  +  * i - , , );
        add( +  * i - ,  +  * i,, exa[i].r - exa[i].l);
        add( +  * i, t, , );
        for(int j=;j<i;j++)
        {
            if (exa[j].r <= exa[i].l) add( +  * j,  +  * i - , , );
        }
    }
    ll cost = ;
    int ans = MaxcostMaxflow(s, t, cost);
    printf("%lld\n", cost);
    return ;
}