[BZOJ]1011 遥远的行星(HNOI2008)

　　由eps引发的血案。

Description

　　直线上N颗行星，X=i处有行星i,行星J受到行星I的作用力，当且仅当i<=A*J。此时J受到作用力的大小为 Fi->j=Mi*Mj/(j-i) 其中A为很小的常量，故直观上说每颗行星都只受到距离遥远的行星的作用。请计算每颗行星的受力，只要结果的相对误差不超过5%即可。

Input

　　第一行两个整数N和A，接下来N行输入N个行星的质量Mi。

Output

　　N行，依次输出各行星的受力情况。

Sample Input

　　5 0.3
　　3
　　5
　　6
　　2
　　4

Sample Output

　　0.000000
　　0.000000
　　0.000000
　　1.968750
　　2.976000

HINT

　　1<=N<=10^5，0.01< a < =0.35，0<=Mi<=10^7。

　　精确结果应该为0 0 0 2 3，但样例输出的结果误差不超过5%，也算对。

Solution

　　奇奇怪怪的乱搞/脑洞题。

　　题目要我们对于每个i求。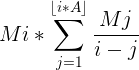

　　网络上有很多关于“A很小，则i*A也很小”而把j变量直接变成0.5*i的题解。

　　小C觉得不是很靠谱，所以小C在这里说一说自己的题解。

　　关键点在于“误差不超过5%”。

　　我们只要让每个的误差不超过5%即可。

　　我们发现，让我们程序复杂度变为O(An^2)的罪魁祸首，就是不断变化的i-j。

　　不妨设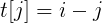，所以我们需要找到一种方法来转化t[j]，

　　使得从求解ans[i]到求解ans[i+1]时，t[j]不会有太多变化，而且误差不能超过5%。

　　我们不妨看看t[j]最多转化到什么程度，使得原式的误差不会超过5%：

　　　　　　

　　　　

　　　　

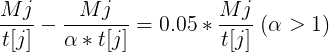
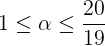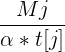　　也就是说，当时，与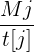的误差不会超过5%。

　　我们注意到对于所有的i，t[j]是连续的正整数。

　　那么问题就很明确了，我们可以构造一个数列a[i]，满足a[1]=1，且a[i+1]是最小的正整数满足a[i+1]*0.95≥a[i]。

　　对于， 我们只需令，就可以将每个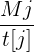的误差控制在5%以内。

　　然后我们就会发现t[j]顿时变得美观了，不妨设为t'[j]，它的定义域被分成连续的若干段。

　　每一段的函数值都一个固定的数，而且函数值在定义域上递减。（不是严格递减，小C口胡一下希望大家能懂）

　　当i变为i-1时，所有t[j]只会减小1。而t'[j]的所有函数段最多只会向左平移一个单位！

　　　　

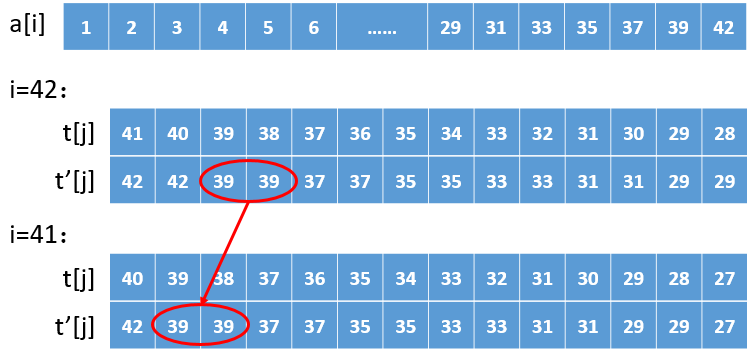
　　所以我们每次改变i，只要维护t'[j]函数值每段的起止端点顺便更新答案即可。

　　时间复杂度是O(n*段数)。

　　那么问题来了，段数究竟是多少呢？其实就是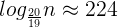段！

　　如果你担心精度不够，还可以把误差控制在1%以内，也就是α取0.99。

　　这样你可能会问，，这时间复杂度有点虚吧？

　　然而别忘了a[i]数列中都是整数，a[i]越小，a[i]/0.99-a[i]就会越小，以至于小于1甚至更小。

　　那么就会出现a[i]~a[i+1]包含了好几段的情况。实际上α=0.99时，段数只有700多段。

　　同理当α=0.95时，段数也不会达到上界，实际只有170多段。

　　注意运算中的精度误差。

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#define MS 1005
#define MN 100005
#define eps 1e-8
using namespace std;
int n,tp,lt;
int pin[MS];
double lim[MS],a[MN],an[MN],ans,m;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

int main()
{
    register int i,j;
    n=read(); scanf("%lf",&m);
    for (lim[]=-,lim[tp=]=;lim[tp]<n;++tp) lim[tp+]=ceil(lim[tp]/0.95);
    for (i=;i<=n;++i) a[i]=read();
    for (i=,j=tp;i<=n;++i)
    {
        while (n-i<=lim[j-]) --j;
        pin[j]=max(pin[j],i);
        if (i<=m*n+eps) ans+=a[i]/lim[j],lt=max(lt,i);
    }
    for (i=n;i;--i)
    {
        for (;lt>m*i+eps;--lt)
            for (j=;j<=tp;++j)
                if (pin[j]<lt) {ans-=a[lt]/lim[j-]; break;}
        for (j=;j<=tp;++j)
        {
            if (!pin[j]) break;
            for (;i-pin[j]<=lim[j-];--pin[j])
                if (pin[j]<=lt) ans-=a[pin[j]]/lim[j],ans+=a[pin[j]]/lim[j-];
        }
        if (ans>=eps) an[i]=ans*a[i]; else an[i]=;
    }
    for (i=;i<=n;++i) printf("%.7lf\n",an[i]);
}

Last Word

　　因为没有在判断j<=i*m时加上eps导致狂WA不止……

　　然后疯狂调参，调α的值发现毫无成效。（小C的算法这么靠谱怎么可能错嘛！）

　　最后居然还厚颜无耻地向管理员要数据……

　　等待管理员回复的当儿，我拿暴力和网上的标程对拍，发现标程都是WA的。

　　而且发现都WA在第20行。（20*0.35=7）

　　然后就加了eps……

　　然后就过了……

　　为此小C还学习了SPJ怎么写。这波不亏。