【XSY2851】蛋糕 数学

题目大意

　　有一个边长为 \(1\) 的正 \(n\) 边形，你要把这个正 \(n\) 边形放到一个正 \(m\) 边形里面，且两个多边形的中心重合。

　　问你这个正 \(m\) 边形的边长最小是多少。

　　\(n,m\leq {10}^9\)

题解

　　对于一种合法的方案，把这个正 \(n\) 边形旋转 \(\frac{2\pi}{m}\) 度之后也能放到这个正 \(m\) 边形里面。

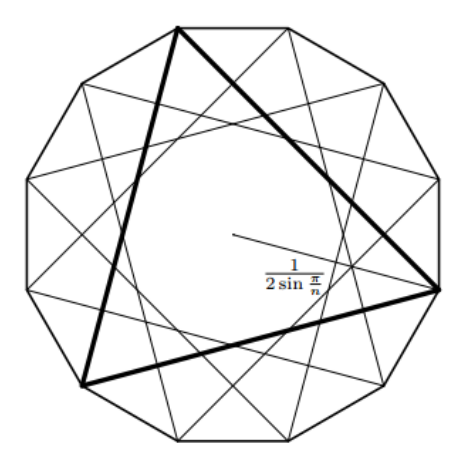
　　那么把所有 \(\frac{m}{\gcd(n,m)}\) 种多边形拼到一起之后就会得到一个 \(\operatorname{lcm}(n,m)\) 边形。

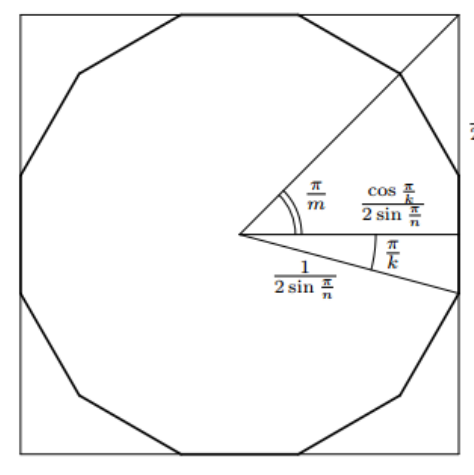
　　现在我们要把正 \(\operatorname{lcm}(n,m)\) 边形塞进一个正 \(m\) 边形。

　　这就很简单了。

　　这个正 \(m\) 边形的每条边对准这个正 \(\operatorname{lcm}(n,m)\) 边形就好了。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<functional>
#include<cmath>
#include<vector>
//using namespace std;
using std::min;
using std::max;
using std::swap;
using std::sort;
using std::reverse;
using std::random_shuffle;
using std::lower_bound;
using std::upper_bound;
using std::unique;
using std::vector;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef std::pair<int,int> pii;
typedef std::pair<ll,ll> pll;
void open(const char *s){
#ifndef ONLINE_JUDGE
	char str[100];sprintf(str,"%s.in",s);freopen(str,"r",stdin);sprintf(str,"%s.out",s);freopen(str,"w",stdout);
#endif
}
void open2(const char *s){
#ifdef DEBUG
	char str[100];sprintf(str,"%s.in",s);freopen(str,"r",stdin);sprintf(str,"%s.out",s);freopen(str,"w",stdout);
#endif
}
int rd(){int s=0,c,b=0;while(((c=getchar())<'0'||c>'9')&&c!='-');if(c=='-'){c=getchar();b=1;}do{s=s*10+c-'0';}while((c=getchar())>='0'&&c<='9');return b?-s:s;}
void put(int x){if(!x){putchar('0');return;}static int c[20];int t=0;while(x){c[++t]=x%10;x/=10;}while(t)putchar(c[t--]+'0');}
int upmin(int &a,int b){if(b<a){a=b;return 1;}return 0;}
int upmax(int &a,int b){if(b>a){a=b;return 1;}return 0;}
const db pi=acos(-1);
ll gcd(ll a,ll b)
{
	return b?gcd(b,a%b):a;
}
ll n,m;
int main()
{
	open("b");
	scanf("%lld%lld",&n,&m);
	db r=1./2/sin(pi/n);
	n=n/gcd(n,m)*m;
	r*=cos(pi/n);
	db ans=r*tan(pi/m)*2;
	printf("%.10f\n",ans);
	return 0;
}