约瑟夫环-循环队列算法（曾微软,google笔试题）

这也是我们聚会时常常做的游戏之一。

算法思路：

　　此处我使用循环链表模拟人围城一圈，每一个结点代表一个人。链表是一个有序链表，链表结点数据域是一个整型，代表人的序号。出局等同于链表删除元素，每次出局后重新从1k开始数。知道剩下最后一个。最后一个的判定是：while((p->num)!=(p->next->num))。循环跳出，就是到最后一个人。

算法代码如下：

 #include <stdio.h>
 #include <stdlib.h>
 #define NUM 5  //游戏人数
 #define OUT 3 // 逢3出局
 struct Person
 {
     int num;
     struct Person *next;
 };
 int main()
 {   int i,j;
     int cnt=;
     int index=;
     int c[NUM]={};
     struct Person person[NUM],*p;
     printf("\n游戏人数是 %d 人\n逢 %d 出局\n\n",NUM,OUT);
     for(i=;i<NUM;i++)
     {
         person[i].num=i+;
         person[i].next=&person[(i+)%NUM];
     }
     p=&person[];
     while((p->num)!=(p->next->num))
     {
         while(cnt<OUT-)
         {
             p=p->next;
             cnt++;
         }
         c[index]=p->next->num;
         index++;
         p->next=p->next->next;
         p=p->next;
         cnt=;
     }
     c[index]=p->num;
     printf("最后一个人是：%d\n\n",p->num);
     printf("出局的顺序是：\n");
     for(j=;j<NUM;j++)
     {
         printf("-->%d",c[j]);
     }
     printf("\n\n");
     system("pause");
     return ;
 }

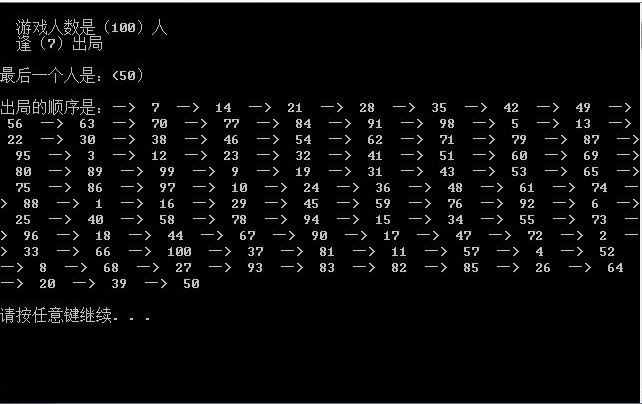
实验截图：