machine learning 之 多元线性回归

整理自Andrew Ng的machine learning课程 week2.

目录：

• 多元线性回归 Multivariates linear regression /MLR
• Gradient descent for MLR
• Feature Scaling and Mean Normalization
• Ensure gradient descent work correctly
• Features and polynomial regression
• Normal Equation
• Vectorization

前提：

$x_{(j)}^{(i)}$：第i个训练样本的第j个特征的值；

$x^{(i)}$：第i个训练样本；

m：训练样本的数目；

n：特征的数目；

1、多元线性回归

具有多个特征变量的回归

比如，在房价预测问题中，特征变量有房子面积x1，房间数量x2等；

模型：

$h_\theta(x)=\theta_0+\theta_1x1+\theta_2x_2+...+\theta_nx_n$

为了方便，认为$x_0=1$（注意这是一个vector，$[x_0^{(1)} x_0^{(2)} ... x_0^{(n)}]=1$），这样的话x和theta就可以相互匹配，进行矩阵运算了；

对于一个training example而言：

$h_\theta(x)$

$=\theta_0+\theta_1x1+\theta_2x_2+...+\theta_nx_n$

=$\theta^Tx$

=$\begin{bmatrix} \theta_0 & \theta_1 & ... & \theta_n \end{bmatrix}  \begin{bmatrix} x_0\\  x_1\\ ...\\ x_n \end{bmatrix}$

对于所有的训练样本而言：

$X=\begin{bmatrix}  x_0^(1) & x_1^(1) & ...& x_n^(1)\\   x_0^(2) & ... &  ... & ...\\    ... & ... &  ... & ...\\  x_0^(m) & x_1^(m) & ...& x_n^(m) \end{bmatrix}  \qquad  \theta=\begin{bmatrix}  \theta_0\\  \theta_1\\   ...\\   \theta_n \end{bmatrix}$

X是design matrix，$h_\theta(x)=X\theta$

2、Gradient descent for MLR

损失函数：$J(\theta)=\frac{1}{2m} \sum_{i=1}^m(h_\theta(x^{(i)})-y_{(i)})^2 = \frac{1}{2m} (X\theta-y)^T (X\theta-y)$

GD更新准则：

$\theta_j:=\theta_j-\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j$

详细的讲解见之前的博客

3、Feature Scaling and Mean Normalization

思想：确保特征的量级在统一尺度之下

为什么要做feature scaling？

如下图，当特征不在一个尺度之下时，优化时的等高线图相当于一个又长又细的椭圆，此时GD会走的特别曲折，要很久才可以找到最优解；

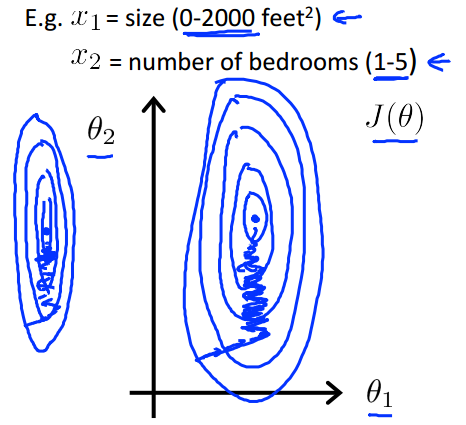
而当特征的尺度一致时，优化时的等高线图是接近一个正圆，GD就会很快的找到最优解；

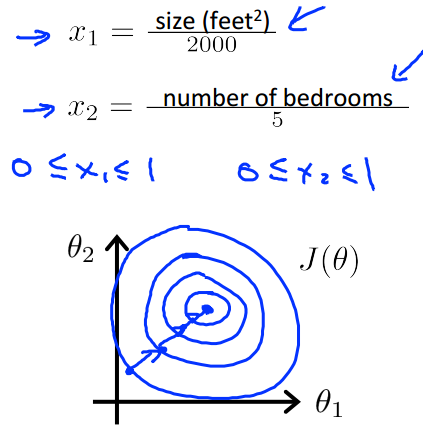
如何做feature scaling？

$x=\frac{x}{max(x)-min(x)}$

这样可以保证x在0到1之间，一般而言，-1<x<1是比较标准的scaling尺度，但是并不是一定要在这个范围之内。

Mean Normalization

结合Feature Scaling ：$x=\frac{x-\mu}{range(x)}$

$\mu$是x的均值，range(x)是最大值与最小值的范围，或者是标准差；

4、Ensure gradient descent work correctly

如何保证我们的Gradient descent是work correctly？可以画一个损失函数随迭代次数变化的图：

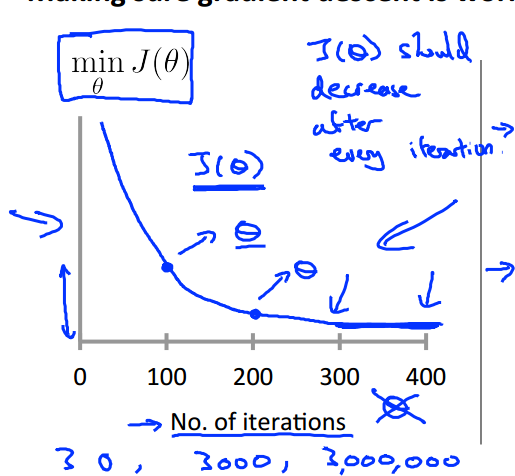
如果GD是做的对的话，那么J应该是下降的，在迭代一定次数后开始收敛。（迭代次数视问题而定，有可能是400，有可能是40，也有可能是4000）

那么怎样才是收敛呢？

在一次迭代中，J下降的十分慢，小于某个很小的阈值（如$10^-3$），但是实际上这个阈值的选择是十分困难的，建议通过J-iteration来调整；

学习率的选取

如果你的J是增大的，那么可能是因为学习率$\alpha$选取的太大了，可以调整$\alpha$；

如果J下降的十分缓慢，说明$\alpha$的选取太小了的，这会消耗很多时间达到收敛；

建议可以通过观察J-iteration图，逐步的调整$\alpha$（0.001，0.003，0.01，0.03，0.1，0.3，1，3.......）；

5、Feature and Polynomial regression

Features

比如在房价预测问题中，若x1是房子的长，x2是房子的宽，此时若组合x1和x2就可以得到一个新的特征area=x1*x2；构造一个好的特征对模型是有帮助的；

Polynomial regression

同上思想，如当线性关系无法精确的拟合散点的话，那应当考虑一些非线性的函数，如quadratic、cubic和square root的关系：

$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3$

$=\theta_0+\theta_1(size)+\theta_1(size)^2+\theta_1(size)^3$

此时：

$x_1=size$

$x_2=size^2$

$x_3=size^3$

同时，在这个时候，Feature Scaling就显得特别重要了：

因为若size<10，则$size^2<100$，$size^3<1000$，

6、Normal Equation

在线性回归问题中，除了可以用GD求最优解，还可以用解析解之间求解，在线性代数中：

$\frac{\partial J}{\partial \theta}=0$是有解析解的：

$\theta=(X^TX)^-1X^Ty$

注意用这种方法求解时，就没必要进行Feature Scaling了；

那既然有解析解了，为什么还要使用Gradient descent呢？

Gradient Descent	Normal Equation
需要进行迭代	无需迭代
需要设定学习率$\alpha$	无需设定学习率$\alpha$
时间复杂度为O(kn2)	时间复杂度O(n3)（主要是求逆的复杂度）

由表中第3点，当数据的特征特别多（n=10⁶）时，Normal Equation会耗费相当多的时间

而且，并非所有的优化问题都要解析解，很多复杂的机器学习问题是没有解析解的，此时我们还是需要使用Gradient Descent来求解

$X^TX$没有逆？

注意到解析解里面有个求逆运算，但是有些情况是没有逆的：

• Redundant features（linearly dependent）

当两个特征是线性依赖的时候，比如size in feet² 和size in m²；

• Too many features（m<=n）

当特征太多了，多于训练样本的数目的时候；

如何解决这个问题？

删除一些特征，或者使用regularization；

注：在matlab/octave中，求逆有inv和pinv两种，而pinv就是在即使没有逆的时候也可以求出来一个逆；

7、Vectorization

　　在求解一个线性回归问题的时候，无论是计算损失，还是更新参数（$\theta$），都有很多的向量计算问题，对于这些计算问题，可以使用for循环去做，但是在matlab/octave，或者python或其他语言的数值计算包中，对向量的计算都进行了优化，如果使用向量计算而不是for循环的话，可以写更少的代码，并且计算更有效率。

　　在上面的一些公式中，都做了vectorization的处理。（主要是计算损失和更新参数）