单源最短路径算法——Dijkstra算法(迪杰斯特拉算法)

一 综述

Dijkstra算法(迪杰斯特拉算法)主要是用于求解有向图中单源最短路径问题。其本质是基于贪心策略的(具体见下文)。其基本原理如下：

(1)初始化：集合vertex_set初始为{source_vertex}，dist数组初始值为$dist[i] = G.arc[source\_vertex][i],i=0,1,\ldots,n-1$

(2)从顶点集合V-vertex_set中选出$v_j$，满足$dist[j] = Min\left\{dist[i] | v_i∈V-vertex\_set\right\}$，那么$v_j$就是当前求得的一条从source_vertex出发的最短路径的终点，并令$vertex\_set = vertex\_set ∪ j$。

(3)修改从source_vertex出发到集合V-vertex_set上任一顶点$v_k$可达的最短路径长度：如果$dist[j] + arc[j][k] < dist[k]$，则令$dist[k] = dist[j] + G.arc[j][k]$。

(4)重复(2)~(3)操作共n-1次，直到所有的顶点都包含在vertex_set中。

具体代码如下：

#include<iostream>
#include<unordered_map>
#include<queue>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<sstream>
#include<set>
#include<map>
using namespace std;
#define MAX_NUM 100
#define INF 0x7fffffff
/*
dijkstra算法的实现
参数说明：
1.source_vertex:表示源点
2.G:表示图(此处以邻接矩阵为例)
3.dist数组：表示源点到其他所有顶点的最短路径的长度。例如dist[j]表示源点到顶点Vj的最短路径长度
4.vertex_set数组：表示已找到最短路径的顶点的集合，其中vertex_set[i] = true表示顶点dist[i]已经最终确定
5.pre数组：用以表示顶点的最短路径的前驱顶点。例如,pre[i] = k表示顶点vi的最短路径上的前驱顶点为vk。
*/
class Graph
{
    public:
    int vertexNum;//顶点个数
    int arcNum;//弧的个数
    int vertex[MAX_NUM];//顶点表
    int arc[MAX_NUM][MAX_NUM] = {{0,INF,10,INF,30,100},
    {INF,0,5,INF,INF,INF},
    {INF,INF,0,50,INF,INF},
    {INF,INF,INF,0,INF,10},
    {INF,INF,INF,20,0,60},
    {INF,INF,INF,INF,INF,0}};//弧信息表
};
void Dijkstra(Graph &G,int source_vertex,int dist[],bool vertex_set[],int pre[])
{
    int _min;
    int k;
    int vertex_num = G.vertexNum;//顶点个数
    //初始化
    for(int i = 0 ; i < vertex_num; i++)
    {
        dist[i] = G.arc[source_vertex][i];//初始化dist数组
        if(i == source_vertex)
            vertex_set[i] = true;//将顶点source_vertex加入vertex_set数组
        else
            vertex_set[i] = false;
        pre[i] = 0;//前驱顶点为v0，后面会更新
    }
    //遍历n-1次，每次找到一个顶点的最短路径
    for(int i = 1; i < vertex_num; i++)
    {
        _min = INF;//初始化辅助变量
        //在未获取最短路径的顶点中，找到离source_vertex最近的顶点vk。
        for(int j = 0; j < vertex_num; j++)
        {
            if(vertex_set[j] == false && dist[j] < _min)
            {
                _min = dist[j];
                k = j;
            }

        }
        //此时源点到顶点vk的最短距离已经找到，即dist[k]已经确定，将k加入到vertes_set中
        vertex_set[k] = true;
        //对dist[j]进行检验更新
        for(int j = 0; j < vertex_num; j++)
        {
            int tmp = (G.arc[k][j]== INF ? INF : _min + G.arc[k][j]);//防止溢出
            if(vertex_set[j] == false && tmp < dist[j])
            {
                dist[j] = _min + G.arc[k][j];//更新满足条件的顶点的dist数组值
                pre[j] = k;//更新前驱顶点
            }
        }
    }

}

int main()
{
    Graph G;
    G.vertexNum = 6;
    int source_vertex = 0;
    int dist[6] = {0};
    bool vertex_set[6];
    int pre[100] = {0};
    Dijkstra(G,source_vertex,dist,vertex_set,pre);
    cout<<dist[0]<<endl;

}

　　

该算法的时间的时间复杂度为O(n^3)，n为图中顶点的个数。其中比较核心的部分是最里面的两个for循环，第一个for循环对应的是第二步；而第二个for循环对应的是第三步；最外层的for循环对应的是第四步。

此外，(1)由于INF表示的int能表示的最大值，它加上一个正值必然会溢出，所以应该考虑溢出的问题。(或者别把INF设成这么大，设小些)

　　   (2)我们默认带权有向图在表示时，若果i == j，则w(i,j)=0而不是w(i,j)=∞。

二 相关理论和注意事项

1.Dijkstra算法的核心之处在于：从源点$v_0$到目标顶点$v_j$的最短路径，要么是弧$(v_0,v_j)$；要么是中间只经过vertex_set中的顶点而最后达到顶点$v_j$的路径。

证明如下：假设符合上述结论的最短路径为L1，假设从$v_0$到顶点$v_j$的最短路径上有一个顶点不在vertex_set中，则说明存在一条终点不在vertex_set中而长度比此路径更短的路径，设该路径为L2。但是，这是与事实相矛盾的。因为我们是按路径长度递增的次序来产生个最短路径的，故长度比此路径短的所有路径都已经产生，它们的终点必然在vertex_set中；即若L2 < L1，L2中的终点必然在集合vertex_set中。

2.更新集合vertex_set只在第二步，相当于每次选出最小的dist[j]，实质就是一个贪心的过程；而第三部相当于更新每个满足条件的dist[j]。第二步和第三步就体现了理论中的两种情况。

3.可以根据pre数组追溯到源点到目标顶点的最短路径序列。　　

4.Dijkstra算法不适用于边上带有负权重的有向图，如果边上有负值的话，有可能出现当与vertex_set内某点(记为A)以负边相连的点(记为B)确定最短路径时，它的最短路径加上负边的权值结果小于A原先确定的最短路径的长度，而此时的A在dijkstra算法下是无法更新的。例如：

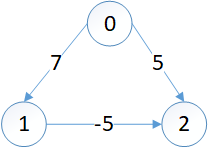
根据Dijkstra算法而言，如果求$v_0$到其他顶点的最短路径的话，首先一开始确定的是$dist[0] = 0$且$vertex\_set[0] = true$，然后由于$dist[2]$是最小的，所以$vertex\_se[2] = true$即$v_0$到$v_2$的最短路径长度为5，然而实际上$v_0$到$v_1$再到$v_2$的距离明显更小，所以实际上$v_0$到$v_2$的最短路径长度为应为7 - 5 = 2；但是$dist[2]$无法再更新了，所以此时利用Dijkstra算法求得的最短路径是错误的。