TSNE数据降维学习【转载】

转自:https://blog.csdn.net/u012162613/article/details/45920827

https://www.jianshu.com/p/d6e7083d7d61

1.思想

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。

此外，t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。

2.例1——鸢尾花数据集降维

# _*_ coding:utf-8 -*-
from sklearn.manifold import TSNE
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

class data():
    def __init__(self, data, target):
        self.data = data
        self.target = target

# 加载数据集
iris = load_iris()
# 共有150个例子， 数据的类型是numpy.ndarray
print(iris.data.shape)
# 对应的标签有0,1,2三种
print(iris.target.shape)
# 使用TSNE进行降维处理。从4维降至2维。
tsne = TSNE(n_components=2, learning_rate=100).fit_transform(iris.data)
# 使用PCA 进行降维处理
pca = PCA().fit_transform(iris.data)
# 设置画布的大小
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.scatter(tsne[:, 0], tsne[:, 1], c=iris.target)
plt.subplot(122)
plt.scatter(pca[:, 0], pca[:, 1], c=iris.target)
plt.colorbar()#使用这一句就可以分辨出，颜色对应的类了！神奇啊。
plt.show()

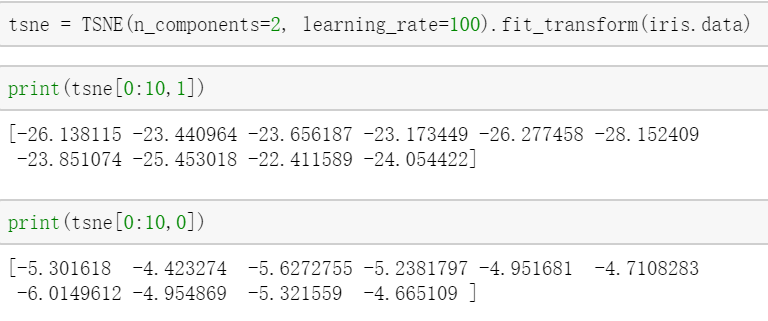
对tsne得到的结果查看，第0维，第1维：

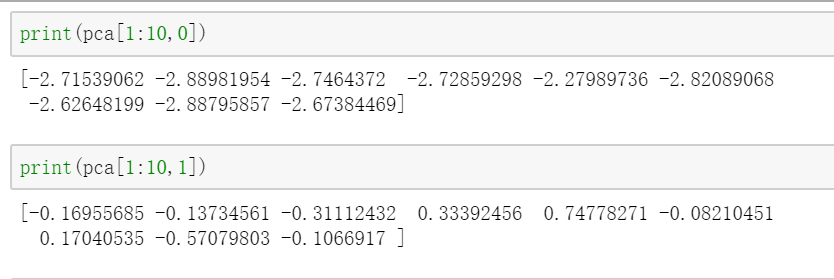
对PCA结果进行查看：

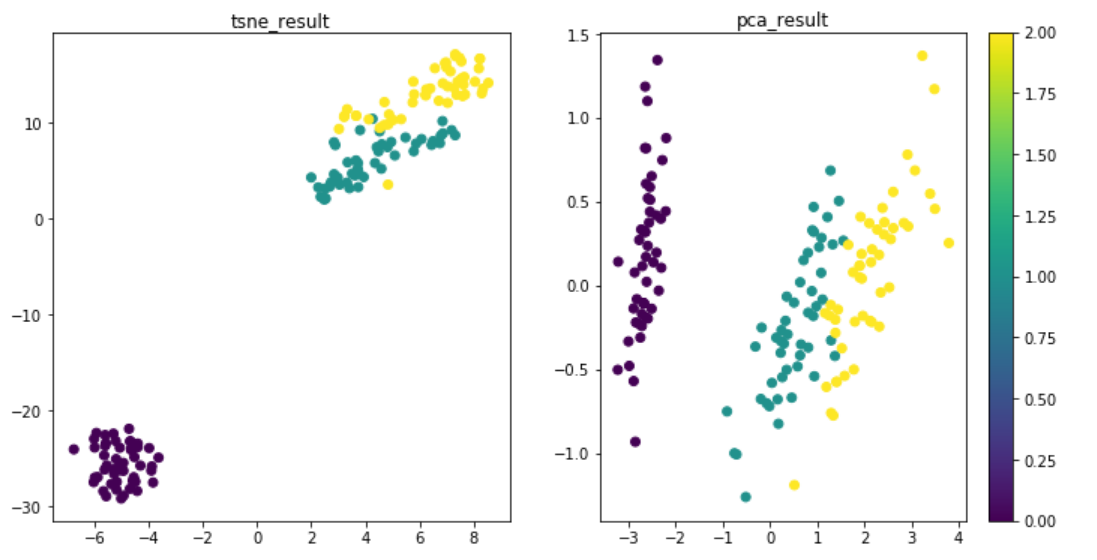
结果：

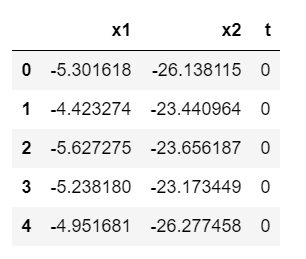
尝试使用Seaborn画图，需要先构造数据框：

import seaborn as sns
import pandas as pd
df=pd.DataFrame(tsne,columns=['x1','x2'])
df['t']=iris.target
df.head()

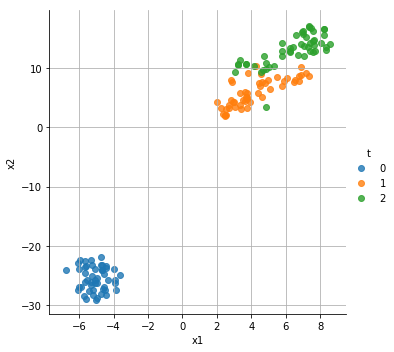
sns.lmplot(x="x1",y="x2",hue="t",data=df,fit_reg=False)
plt.grid(True)

3.例2——MINISET数据集

digits = datasets.load_digits(n_class=5)
X = digits.data
y = digits.target
print X.shape
n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
    ix = 10 * i + 1
    for j in range(n_img_per_row):
        iy = 10 * j + 1
        img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))

#取前400个,按行放置
#img中会有0、10、20列这些没有，是为了形成空列吧。

plt.imshow(img, cmap=plt.cm.binary)#cmap: 颜色图谱（colormap), 默认绘制为RGB(A)颜色空间。
plt.title('A selection from the 64-dimensional digits dataset')

import time#需导入包
tsne = TSNE(n_components=3, init='pca', random_state=0)
t0 = time
X_tsne = tsne.fit_transform(X)
plot_embedding2D(X_tsne[:,0:2],"t-SNE 2D")
plot_embedding3D(X_tsne,"t-SNE 3D (time %.2fs)" %(time - t0))

//最终画图的代码， 没有运行起来，不太会。

 博主给的结果：

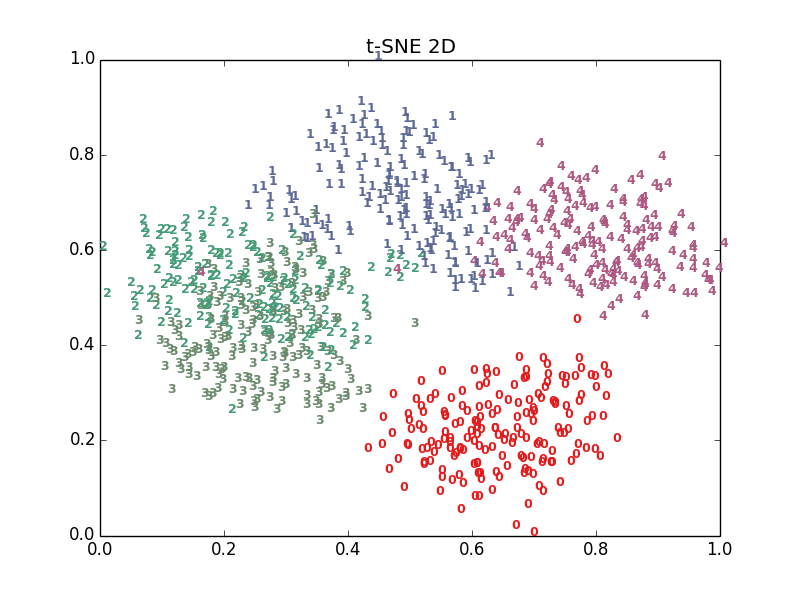
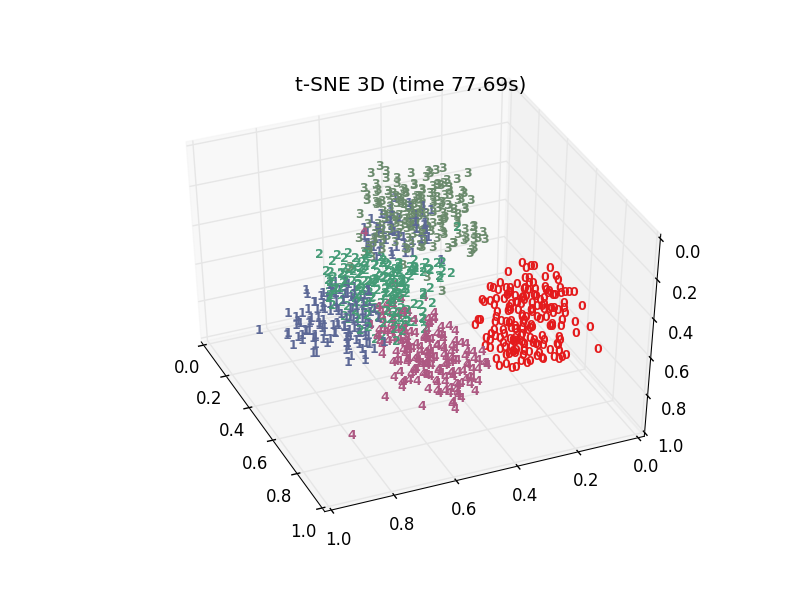
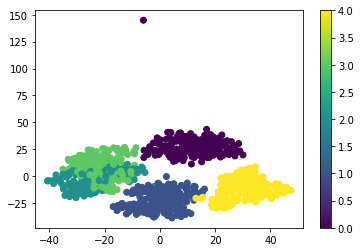
我使用散点图画出的二维结果：

plt.scatter(X_tsne[:,0],X_tsne[:,1],c=Y)
plt.colorbar()

2020-5-8更新—————— 

1.http://www.datakit.cn/blog/2017/02/05/t_sne_full.html，其实这个讲的一般。

http://bindog.github.io/blog/2016/06/04/from-sne-to-tsne-to-largevis/

2020-5-13周三更新——————————

1.SNE原理

https://zhuanlan.zhihu.com/p/57937096，讲的不错。

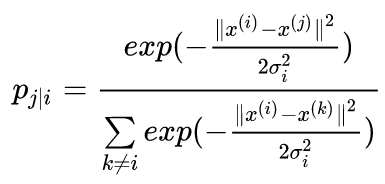
这是在高维空间中，通过仿射将欧几里得距离转换为点之间的相似性的概率分布，p值越大，表示i和j之间的相似性越高，其实也就是表示欧氏距离越小了。高维空间中使用的是高斯分布。

而未知的低维空间中也建立这么一个 分布，sne中使用的同样是高斯分布：

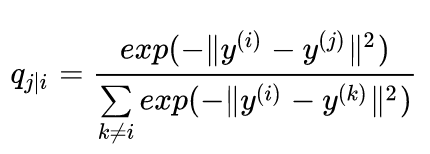
这样的话，想让两个空间中的分布尽可能相似相等，所以使用KL散度来度量：

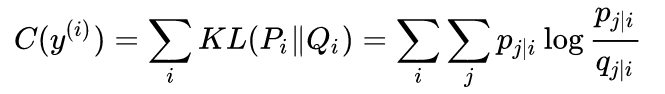
而我们可以看到，KL散度它是不对称的，它是有偏向性的，所以导致了SNE也有偏向性：当p较大，而q较小时损失之较大，翻译过来也就是点在高维空间中相似度较高，但低维空间相似度较小时，损失会比较大；那么sne就会倾向于选择高维空间中距离较远的，而低维空间中距离较近的，所以就说它倾向于保留数据的局部结构（这个时针对于低维空间来说的）。

//但我还是有点想不通，保留这个词不应该针对已知的高维空间吗？高维空间的局部结构不就是点尽可能地相似吗？总之这里感觉很矛盾，保留疑问。

//感觉上面这句话的意思是说，局部特征是针对于低维空间说的，全局结构是针对高维空间说的。所以就说sne更关注于低维空间，也就是局部特征？

2.SNE求解

那么上面主要的参数就是sigma，怎么求呢？

复杂度：

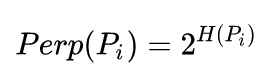
也就是困惑度，可以理解为某个数据点附近有效近邻点的个数。困惑度通常在5-50之间。Hp公式如下：

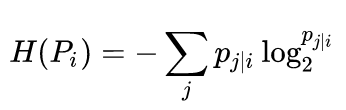
那么在确定了困惑度值之后，就可以根据Hp来计算sigma了。（感觉挺难计算的。）

损失函数对y求梯度：

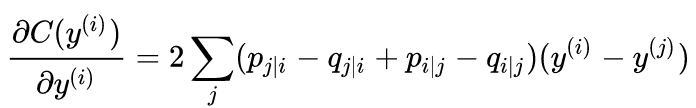
因为我们最终要求的就是yi，数据在2/3维空间中的表示，所以要对它们求梯度啊。

//但是梯度这个计算公式是怎么求的，我还不会。

3.对称TSNE

它使用联合概率分布，所以就是对称的？这一点我还不太懂。

4.t-SNE

//这里的t表示的是t分布，低维空间使用t分布来衡量。

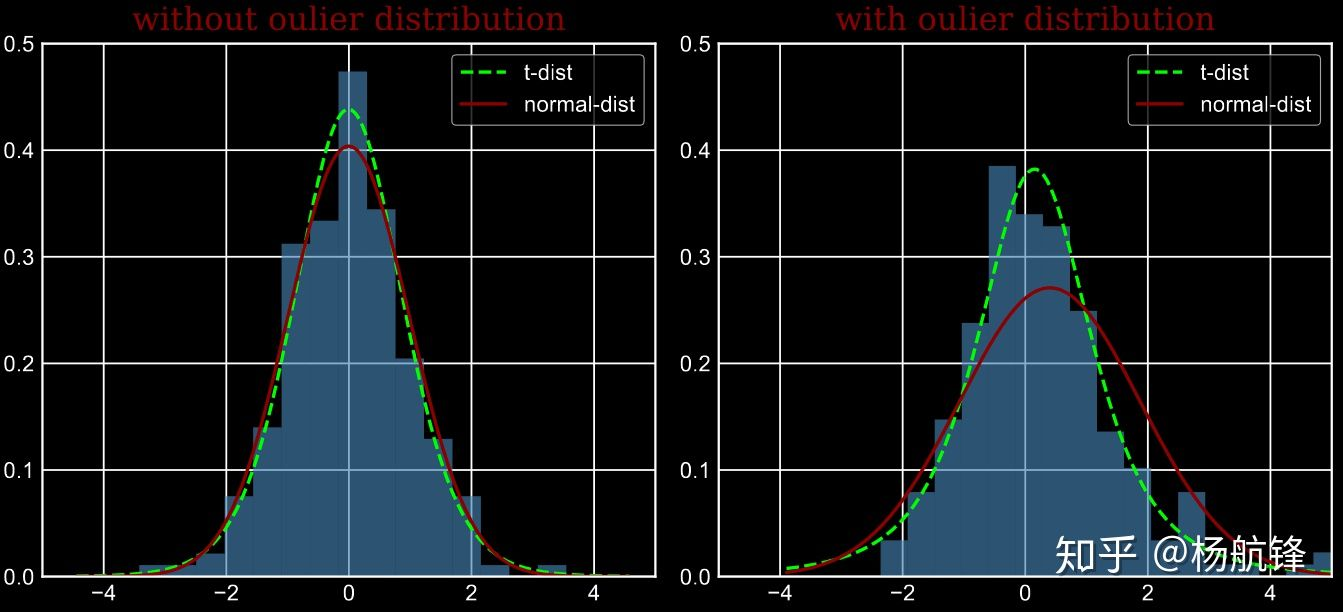
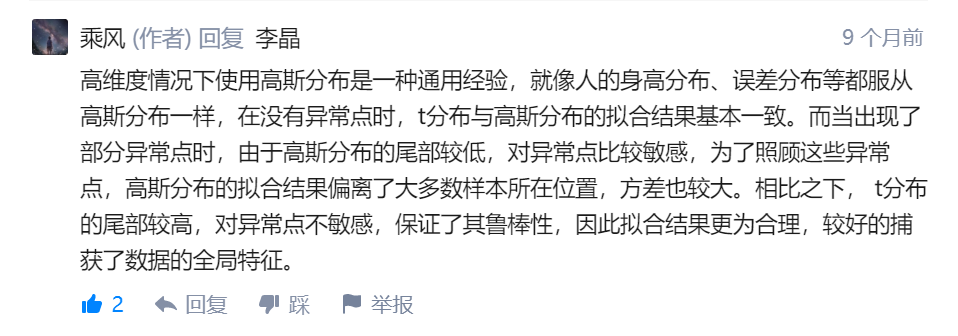
从上面的图和作者的回复来看，因为高斯分布尾部较低对异常值敏感，如果有异常值的话，那么均值方差就会受到影响，曲线形状会照顾那些异常点，而t分布就尾部比较高，对异常点相对不敏感。学习了。而为什么会有异常点出现呢。因为高维降到低维会存在一个拥挤的问题，t可以来缓解这个问题。

使用t分布，低维空间如下：

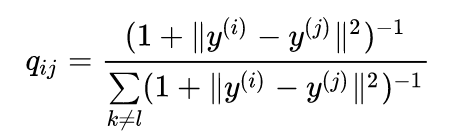
总之，t-sne的改进是：

它主要就是用来可视化。