系列解读Dropout

本文主要介绍Dropout及延伸下来的一些方法，以便更深入的理解。

想要提高CNN的表达或分类能力，最直接的方法就是采用更深的网络和更多的神经元，即deeper and wider。但是，复杂的网络也意味着更加容易过拟合。于是就有了Dropout，大部分实验表明其具有一定的防止过拟合的能力。

1- Dropout

最早的Dropout可以看Hinton的这篇文章 
《Improving neural networks by preventing co-adaptation of feature Detectors》

从文章的名字我们就可以先对Dropout的工作原理有个猜测：过拟合意味着网络记住了训练样本，而打破网络固定的工作方式，就有可能打破这种不好的记忆。

Ok，我们直接来看什么是Dropout：

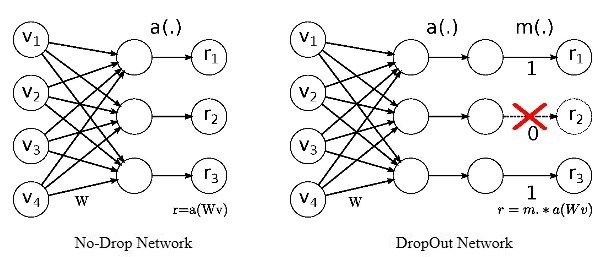
需要注意的是：论文中Dropout被使用在全连接层之后，而目前的caffe框架中，其可以使用在各种层之后。

如上图左，为没有Dropout的普通2层全连接结构，记为 r=a(Wv)，其中a为激活函数。

如上图右，为在第2层全连接后添加Dropout层的示意图。即在 模 型 训 练 时 随机让网络的某些节点不工作（输出置0），其它过程不变。

对于Dropout这样的操作为何可以防止训练过拟合，原作者也没有给出数学证明，只是有一些直观的理解或者说猜想。下面说几个我认为比较靠谱的解释：

(1) 由于随机的让一些节点不工作了，因此可以避免某些特征只在固定组合下才生效，有意识地让网络去学习一些普遍的共性（而不是某些训练样本的一些特性）

(2) Bagging方法通过对训练数据有放回的采样来训练多个模型。而Dropout的随机意味着每次训练时只训练了一部分，而且其中大部分参数还是共享的，因此和Bagging有点相似。因此，Dropout可以看做训练了多个模型，实际使用时采用了模型平均作为输出 
（具体可以看一下论文，论文讲的不是很明了，我理解的也够呛）

训练的时候，我们通常设定一个dropout ratio = p,即每一个输出节点以概率 p 置0(不工作)。假设每一个输出都是相互独立的，每个输出都服从二项伯努利分布B(1-p)，则大约认为训练时 只使用了 (1-p)比例的输出。

测试的时候，最直接的方法就是保留Dropout层的同时，将一张图片重复测试M次，取M次结果的平均作为最终结果。假如有N个节点，则可能的情况为R=2^N,如果M远小于R，则显然平均效果不好；如果M≈N，那么计算量就太大了。因此作者做了一个近似：可以直接去掉Dropout层，将所有输出 都使用 起来，为此需要将尺度对齐，即比例缩小输出 r=r*(1-p)。 
即如下公式：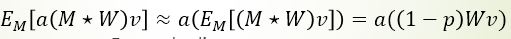 
 
特别的， 为了使用方便，我们不在测试时再缩小输出，而在训练时直接将输出放大1/(1-p)倍。

结论： Dropout得到了广泛的使用，但具体用到哪里、训练一开始就用还是后面才用、dropout_ratio取多大，还要自己多多尝试。有时添加Dropout反而会降低性能。

2- DropConnect

DropConnect来源于《Regularization of Neural Networks using DropConnect》这篇文章。

更详细的实验对比以及代码，可以点击http://cs.nyu.edu/~wanli/dropc/

该方法改进于第一节介绍的Dropout,具体可看下图作对比

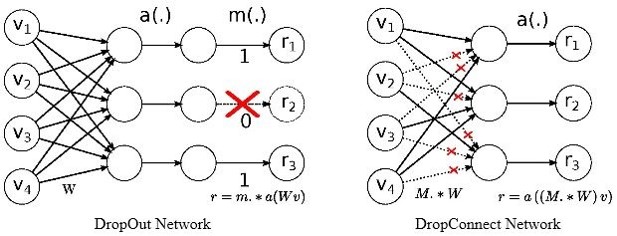
由图可知，二者的区别很明显：Dropout是将输出随机置0，而DropConnect是将权重随机置0。 
文章说之所以这么干是因为原来的Dropout进行的不够充分，随机采样不够合理。这可以从下图进行理解：

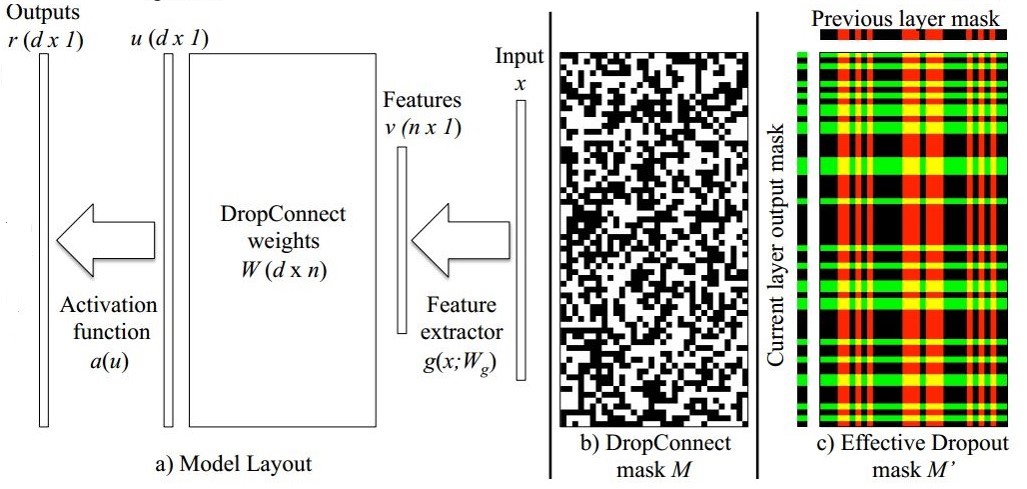
如上图所示，a表示不加任何Drop时的一层网络模型。添加Drop相当于给权重再乘以一个随机掩膜矩阵M。

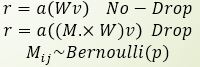
不同的是，DropConnect由于直接对权重随机置0，因此其掩膜显得更加具有随机性，如b所示。而Dropout仅对输出进行随机置0,因此其掩膜相当于是对随机的行和列进行置0，如c所示。

训练的时候，训练过程与Dropout基本相同。

测试的时候，我们同样需要一种近似的方法。如下图公式所示：

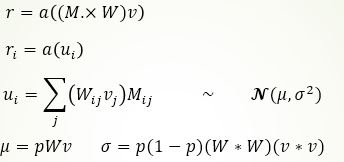
注意： 掩膜矩阵M的每一个元素都满足二项伯努利分布。假如M的维度为m*n，则可能的掩膜有2^(m*n)种，之前提到过我们可以粗暴的遍历所有的掩膜然后计算结果最后求平均。中心极限定理：和分布渐进于正态分布。 于是，我们可以不去遍历，而是通过计算每一维的均值与方差，确定每一维的正态分布，最后在此正态分布上做多次采样后求平均即可获得最终的近似结果。

具体测试时的算法流程如下：

其中，Z是在正态分布上的采样次数，一般来说越大越好，但会使得计算变慢。

实验： 作者当然要做很多对比试验，但其实发现效果并不比Dropout优秀太多，反而计算量要大很多，因此到目前DropConnect并没有得到广泛的应用。具体的对比，可以参看原文，这里我只贴一张图来说明对于Drop ratio的看法：

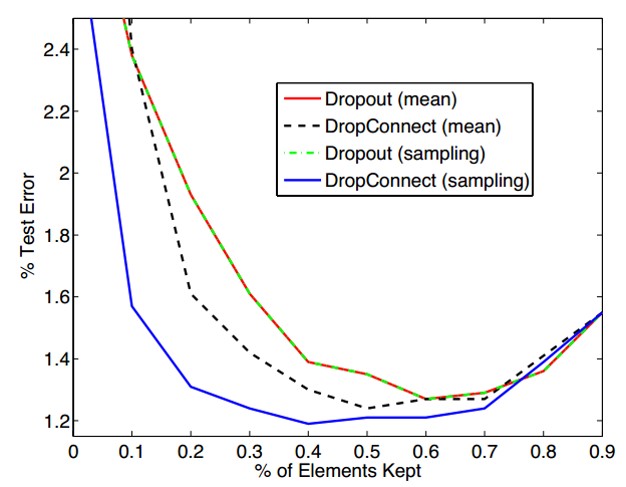
由此可以看出，drop ratio并不是越大越好，具体需要大家多做实验多体会。