参数估计（1）：从最小二乘到最小b乘

机器学习到底学习到了什么，或者说“训练”步骤到底在做些什么？在我看来答案无非是：所谓的“学习”就是把大量的数据归纳到少数的参数中，“训练”正是估计这些参数的过程。所以，除了“参数估计”， 我想不到还有什么更适合用来首先讨论的了。

1.起源

“1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星…高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》。”--维基百科

据说这就是参数估计的起源。

2.最小二乘法

那么就先来看看历史最悠久的最小二乘法吧！我们假设皮亚奇是一个非常勤奋又热爱熬夜的人（天文学家大概都是这样的）， 在能够观测到谷神星的40天里，他每天晚上都架起望远镜观测他的这颗小行星，一边不忘天文学家的老本行：记录下该小行星的位置。皮亚奇当然不大可能直接得到小行星在太阳系内的坐标，不过只要他能够记录下当前时间和目标相对于地表的高度与角度，再知道自己的经纬度与地球的运行轨道，就完全可以推算出谷神星的在太阳系内的坐标。为了把问题简化，假设我们已经拿到了皮亚奇的最终坐标，一个男人四十天的辛苦结晶：

可怜的皮亚奇只观测到了一部分轨道，谷神星就转到太阳的背后去了，留下了一个估计全轨道的问题。鉴于开普勒早在本事件发生前300年就去世了，因此无论高斯还是其他竞争者都应当清楚行星的运行轨道是一个椭圆，其一般方程只有五个参数：

（1）

取得了皮亚奇的观测数据(x,y)之后，这个椭圆方程就是一个关于参数的5元1次超定方程组。线性超定方程组的矩阵形式是：

（2）

稍有了解的同学应该都知道它的解公式是：

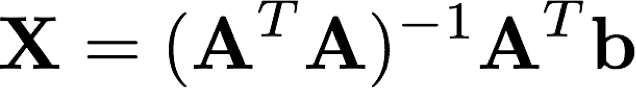
这个解是怎么来的呢？让我们把它稍作变换，写成：

这又是什么？其实等式左边就是下面这个式子对X的导数：

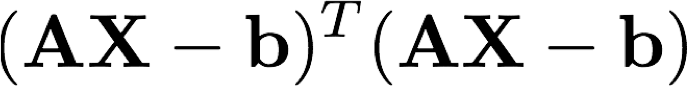
这是超定方程组左边和右边差值的平方！令其导数等于0，就是求一个X使得误差的平方最小。撇开线性代数的框架，我们再回到(1),事实上就是求一个满足下式的解：

使得误差的平方和最小，这也就是最小二乘(Least Squares)名字的由来。按照（2）的思路，计算的是椭圆公式(1)左边和右边的代数距离，因此这类方法叫做代数距离(algebra distance)最小二乘; 因为模型f是关于参数a的线性函数，所以又叫做线性最小二乘(linear least square).

好了，我们也可以估计小行星的轨道了，并且用的就是高斯的最小二乘思想。但是严格的来说，高斯本人的做法稍有区别。我们使用的线性最小二乘只是最小二乘法最简单的一个特例。它并没有真正的关心“观测数据和椭圆曲线的拟合程度“，而只是关心“观测数据和椭圆方程的拟合程度”，因此时常得到不稳定的结果。而高斯心中想的显然更合理，他要“使每个观测点到椭圆曲线距离的平方和最小”，而不是“使椭圆公式左边和右边差值的平方和最小”：

如此一来，模型就不再是待估参数的线性函数了，所以这种方法属于非线性最小二乘(non-linear least squares)；又因为目标函数限制的是实实在在的几何距离，因此又叫做几何距离(geometric distance)最小二乘。我在这里不打算复刻高斯的工作，因为我觉得求一点到椭圆的距离并对其进行最优化真的很难。还是让我们看看线性最小二乘法的结果吧！

蓝色的点是皮亚奇观测的40个数据(不用谢，是我伪造的)，黑线是真正的小行星轨道，红线是线性最小二乘法估计出来的轨道。嘿，下次我们也应该去预测小行星轨道了，效果看起来还行不是么？

3.最小b乘法

可是为什么效果还行呢，为什么不是最小一乘法或者最小三乘法比较好？要回答这个问题，椭圆拟合显得过于复杂了，我们需要一个计算起来更简单的例子：直线拟合，或者说线性回归(linear regression)。

假设我们观测到一列二维点并要用它们来回归一条直线：

为了计算上的方便，我们来做一个更强但不改变问题性质的限制：假设x的值是完全准确的，只有y包含了一定的观测误差。为了体现这一点，我用几行代码，取了x=1到10十个点，然后按一条直线方程产生对应的y，最后再在每个y上加上一个代表观测误差的高斯噪声。

现在来用最小二乘法回归这条直线方程。我们要做的事实上就是求一组斜率k和截距b，使得y的观测值和真值之间的误差平方和最小：

好了，就这么简单。此处先按下不表，我们再回头来看看数据的产生过程。因为x是预先固定的，而y是通过线性变化加上一个高斯分布产生的，因此事实上数据产生的概率是：

将高斯分布的公式代入上式我们得到：

我们把指数中的求和项单独拿出来：

看出来什么没有？这就是刚才写出的最小二乘法的目标函数。

也就是说，最小二乘估计的意义在于且仅在于：如果数据的观测误差是高斯分布的，那么最小二乘解就是使得观测数据的出现概率最大的解。

而一旦观测误差不是高斯分布的，最小二乘估计就失去了它独特的地位。例如，早在高斯发明最小二乘法之前几十年，最小一乘法就已经出现了，它对应的是观测误差服从拉普拉斯分布。

除了高斯分布和拉普拉斯分布，有很多别的可能可能。有一个叫做广义误差分布(exponential power distribution)的的概率分布总结了一大类情况： 

其中u是均值，a是和方差相关的一个参数，b是尺度参数。我们所熟悉的高斯分布就是b=2的广义误差分布，而拉普拉斯分布正是b=1的情况。b当然还可以取其他值，甚至是小数，这就使得广义误差分布描述了一大类中间高两边低连续且对称的概率密度函数。把刚才对线性回归的讨论稍微推广一下，我们就能得出这样的结论：只要一个系统的观测误差服从尺度为b的广义误差分布，那么最小b乘解就是使其观测数据出现概率最大的解。

可是广义误差分布允许无数种可能的尺度，为什么只有最小二乘法才被最广泛的应用呢？

一来，这要归功于拉普拉斯证明了中心极限定理，即：任何随机误差（不包括系统误差），如果是由多种独立的微小误差相加组合而成的，那么它的分布一定趋近于高斯分布。现实生活中大部分的观测误差来源都较为复杂，可以看成多种微小误差的叠加。例如我们可以想象皮亚奇的误差来自于空气不好+镜片不好+眼歪+手抖+那美克星超新星爆发…等等，它的总体概率分布趋近于高斯分布，因此最小二乘法会取得最好的效果。

二来，其实也有很多数据是不符合高斯分布的，例如机器学习中常常提到的长尾(long tail)的数据,经常服从拉普拉斯分布，对他们来说最小一乘才是更好的解法。但是最小一乘法的目标函数中有一个绝对值，这对优化算法来说非常不友好。所以虽然最小一乘法比最小二乘法发明的更早，但是直到二十世纪最优化算法得到了长足的发展之后，最小一乘法才逐渐受到重用。

而所有这些最小b乘法中所暗含的“使得观测数据出现概率最大”的道理，直到高斯发明最小二乘法的一百年之后，才由现代统计学的奠基人罗纳德.费希尔总结归纳成：极大似然估计(maximize likelihood estimation)，我们下一节讨论。