750. Number Of Corner Rectangles四周是点的矩形个数

［抄题］：

Given a grid where each entry is only 0 or 1, find the number of corner rectangles.

A corner rectangle is 4 distinct 1s on the grid that form an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1s used must be distinct.

Example 1:

Input: grid =
[[1, 0, 0, 1, 0],
 [0, 0, 1, 0, 1],
 [0, 0, 0, 1, 0],
 [1, 0, 1, 0, 1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].

Example 2:

Input: grid =
[[1, 1, 1],
 [1, 1, 1],
 [1, 1, 1]]
Output: 9
Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.

Example 3:

Input: grid =
[[1, 1, 1, 1]]
Output: 0
Explanation: Rectangles must have four distinct corners.

[暴力解法]：

时间分析：

空间分析：

[优化后]：

时间分析：

空间分析：

［奇葩输出条件］：

［奇葩corner case］：

［思维问题］：

已经中毒了，感觉什么都要用dp：能数学直接解决的话就不麻烦了

［英文数据结构或算法，为什么不用别的数据结构或算法］：

没有，就是直接在矩阵上数

［一句话思路］：

找矩形就是找两行+两列，拆开

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

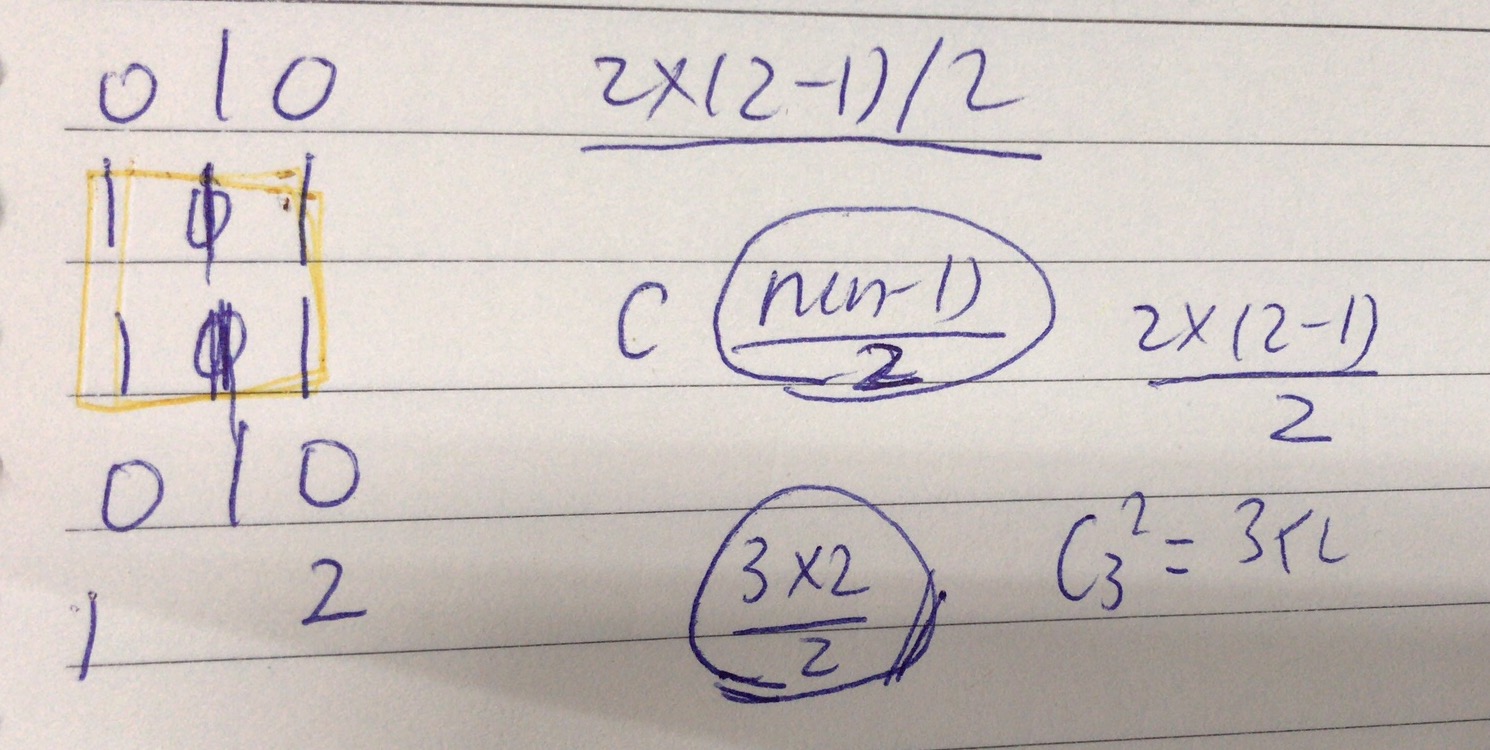
［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

每一对 i j 算一次，所以res += count*(count - 1) / 2应该在j更新的紧随其后

［总结］：

可以用数学就不用强行套用dp

［复杂度］：Time complexity: O(n^3) Space complexity: O(1)

［算法思想：递归/分治/贪心］：

［关键模板化代码］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

class Solution {
    public int countCornerRectangles(int[][] grid) {
        //cc: null
        if (grid == null || grid.length == 0) return 0;
 
        int res = 0;
        int count = 0;
 
        //for loop: 2 rows, count = cols
        for (int i = 0; i < grid.length - 1; i++) {
            for (int j = i + 1; j < grid.length; j++) {
                count = 0;
                for (int k = 0; k < grid[0].length; k++) {
                    if (grid[i][k] == 1 && grid[j][k] == 1) count++;
                }
                if (count > 1) res += count * (count - 1) / 2;
            }
        }
 
        return res;
    }
}