poj2549 Sumsets

Sumsets

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11886		Accepted: 3273

Description

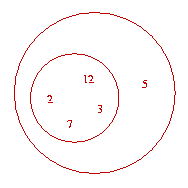Given S, a set of integers, find the largest d such that a + b + c = d where a, b, c, and d are distinct elements of S.

Input

Several S, each consisting of a line containing an integer 1 <= n <= 1000 indicating the number of elements in S, followed by the elements of S, one per line. Each element of S is a distinct integer between -536870912 and +536870911 inclusive. The last line of input contains 0.

Output

For each S, a single line containing d, or a single line containing "no solution".

Sample Input

5
2
3
5
7
12
5
2
16
64
256
1024
0

Sample Output

12
no solution

Source

Waterloo local 2001.06.02

大致题意：在集合S中找到4个互不相同的数，使得a + b = d - c,输出最大的d.

分析：meet in the middle的裸题.方程模型，将a+b存进hash表中，然后枚举d,c找一下就好了.为了使得4个数不相同，还必须记录一下a+b中的a,b.询问的时候判断a,b,c,d是否互不相同.

          我用map竟然T掉了......hash表跑进100ms内......期间还犯了一个脑残错误：当找到了答案后我只退出了内层循环，没有退出外层循环，结果WA了半天.以后写for还是尽量带括号吧，删减的话到最后在弄.

#include <cstdio>
#include <map>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int mod = ;

int n,a[],head[],nextt[],X[],Y[],w[],tot = ;
bool flag = false;

void add(int x,int y)
{
    int temp = (((x + y) % mod) + mod) % mod;
    X[tot] = y;
    Y[tot] = x;
    nextt[tot] = head[temp];
    head[temp] = tot++;
}

bool query(int x,int y)
{
    int temp = (((x - y) % mod) + mod) % mod;
    for (int i = head[temp]; i + ; i = nextt[i])
        if (X[i] != y && Y[i] != x && (X[i] + Y[i]) == (x - y) && X[i] != x && Y[i] != y)
            return true;
    return false;
}

int main()
{
    while (scanf("%d",&n) != EOF && n)
    {
        flag = false;
        tot = ;
        memset(head,-,sizeof(head));
        memset(X,,sizeof(X));
        memset(Y,,sizeof(Y));
        for (int i = ; i <= n; i++)
            scanf("%d",&a[i]);
        sort(a + ,a +  + n);
        for (int i = ; i <= n; i++)
            for (int j = i + ; j <= n; j++)
                add(a[i],a[j]);
        for (int i = n; i >= ; i--)
        {
            for (int j = i - ; j >= ; j--)
                if (query(a[i],a[j]))
                {
                    flag = ;
                    printf("%d\n",a[i]);
                    break;
                }
            if (flag)
                break;
        }
        if (!flag)
            puts("no solution");
    }

    return ;
}