如果一对兔子每月生一对兔子；一对新生兔，从第二个月起就开始生兔子；假定每对兔子都是一雌一雄，试问一对兔子，第n个月能繁殖成多少对兔子？

———————————————————————————————————————————————————————————————————

典型斐波那契数列，用递归实现是so easy,在JS中实现递归通常用arguments.callee

这是因为早期JS没有具名函数，无法使用函数名进行递归，于是产生了arguments.callee

JS严格模式禁用了arguments.callee，这意味着无法在匿名函数中调用自身。

为什么要禁用呢？因为普通写法性能上比arguments更优，而且arguments.callee 还会带来函数引用优化问题和尾递归优化的问题

————————————————————————————————————————————————————————————————————

上述兔子问题，用递归的话，不到100次递归成功搞垮了我的浏览器，函数调用的次数呈指数级增长，性能堪忧，所以，，，，下面是斐波那契的非递归实现：

用迭代消除递归：

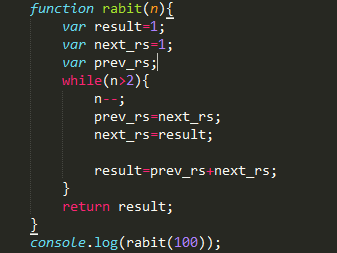
性能提升了几百万倍甚至更多

callee和斐波那契数列的更多相关文章

  1. C#求斐波那契数列第30项的值（递归和非递归）

    using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...

  2. 斐波拉契数列加强版——时间复杂度O(1)，空间复杂度O(1)

    对于斐波拉契经典问题,我们都非常熟悉,通过递推公式F(n) = F(n - ) + F(n - ),我们可以在线性时间内求出第n项F(n),现在考虑斐波拉契的加强版,我们要求的项数n的范围为int范围 ...

  3. js中的斐波那契数列法

    //斐波那契数列:1,2,3,5,8,13…… //从第3个起的第n个等于前两个之和 //解法1: var n1 = 1,n2 = 2; for(var i=3;i<101;i++){ var ...

  4. 剑指Offer面试题：8.斐波那契数列

    一.题目:斐波那契数列 题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项.斐波那契数列的定义如下: 二.效率很低的解法 很多C/C++/C#/Java语言教科书在讲述递归函数的时 ...

  5. 算法: 斐波那契数列C/C++实现

    斐波那契数列: 1,1,2,3,5,8,13,21,34,....     //求斐波那契数列第n项的值 //1,1,2,3,5,8,13,21,34... //1.递归: //缺点:当n过大时,递归 ...

  6. 洛谷P1962 斐波那契数列 || P1349 广义斐波那契数列[矩阵乘法]

    P1962 斐波那契数列 大家都知道,斐波那契数列是满足如下性质的一个数列: • f(1) = 1 • f(2) = 1 • f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数 ...

  7. Python递归及斐波那契数列

    递归函数 在函数内部,可以调用其他函数.如果一个函数在内部调用自身本身,这个函数就是递归函数.举个例子,我们来计算阶乘 n! = 1 * 2 * 3 * ... * n,用函数 fact(n)表示,可 ...

  8. 简单Java算法程序实现！斐波那契数列函数~

    java编程基础--斐波那契数列 问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 思路:可能出现的情况:(1) n=1 ,一种方法 ;(2)n=2 ...

  9. js 斐波那契数列（兔子问题）

    对于JS初学者来说,斐波那契数列一直是个头疼的问题,总是理不清思路. 希望看完这篇文章之后会对你有帮助. 什么是斐波那契数列 : 答: 斐波那契数列,又称黄金分割数列.因数学家列昂纳多·斐波那契(Le ...

随机推荐

  1. Armstrong公理

    从已知的一些函数依赖,可以推导出另外一些函数依赖,这就需要一系列推理规则,这些规则常被称作“Armstrong 公理”. 设U 是关系模式R 的属性集,F 是R 上成立的只涉及U 中属性的函数依赖集. ...

  2. Java调用.NET 的Web Service服务故障排除

    参考路径:http://blog.sina.com.cn/s/blog_4c925dca01014y3r.html

  3. windows git支持arc命令

    本文整理了在Windows系统上安装代码审查工具Arcanist的过程.目的是配合Phabricator进行代码review.配置成功后可使用arc diff命令来发起code review. 1.安 ...

  4. 【python练习题】程序9

    #题目:暂停一秒输出. import time for i in range(5): print (i) time.sleep(1)

  5. 在web-inf外面 使用的是绝对路径进行访问 “/”表示访问文件夹 一层一层方式 我们在windos下访问文件夹也是一层一层的访问

  6. linux硬件数据

    Linux 文件详解 lrwxrwxrwx root root 8月 bin -> usr/bin //二进制目录 存放了许多GNU用户极工具 dr-xr-xr-x. root root 8月 ...

  7. 在idea中设置记住git的用户名和密码

    在idea中设置记住git的用户名和密码 1.在项目根目录下执行以下git命令: git config --global credential.helper store 2.执行上述命令后,在idea ...

  8. Linux各目录及每个目录的详细介绍

    http://www.cnblogs.com/duanji/p/yueding2.html

  9. 使用开源项目xutils3完成下载

    上一次自己写了一个多线程断点续传下载的demo,过于麻烦,bug超多,所以我学习使用xutils来完成此功能. 先将xutils依赖搭建好(上一篇博客已经具体写了方法) 先看看效果图: 下面开始代码的 ...

  10. 【XSY2720】区间第k小 整体二分 可持久化线段树

    题目描述 给你你个序列,每次求区间第\(k\)小的数. 本题中,如果一个数在询问区间中出现了超过\(w\)次,那么就把这个数视为\(n\). 强制在线. \(n\leq 100000,a_i<n ...