MT【253】仿射和蒙日圆
如图,设点$M(x_0,y_0)$是椭圆$C:\dfrac{x^2}{2}+y^2=1$上一点,从原点$O$向圆$M:(x-x_0)^2+(y-y_0)^2=\dfrac{2}{3}$作两条切线分别与椭圆$C$交于$P,Q$,直线$OP,OQ$的斜率分别为$k_1,k_2$
(1)求证:$k_1k_2$为定值
(2)求四边形$OPQM$面积的最大值.
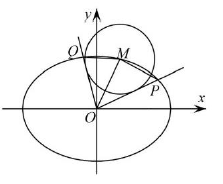

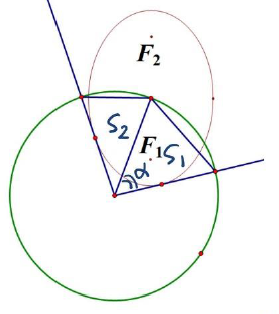
分析:涉及到面积最大容易想到仿射变换:
(1)
$$\begin{cases}
x^{'}&=x\\
y^{'}&=\sqrt{2}y
\end{cases}$$
则$k^{'}=\sqrt{2}k$,由蒙日圆性质得$k_1^{'}k_2^{'}=-1$故$k_1k_2=-\dfrac{1}{2}$
(2)如图$S=\dfrac{1}{\sqrt{2}}(S_1+S_2)=\dfrac{1}{\sqrt{2}}(sin\alpha+cos\alpha)\le1$
第二小问常规方法提示:

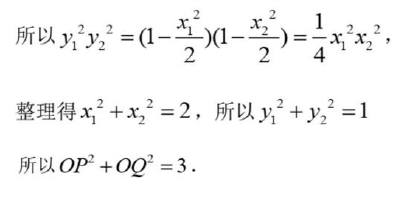
MT【253】仿射和蒙日圆的更多相关文章
- MT【290】内外圆求三角最值
求$\sqrt{\dfrac{5}{4}-\sin x}+2\sqrt{\dfrac{9}{4}+\cos x-\sin x}$的最小值. 提示:$\sqrt{\dfrac{5}{4}-\sin x} ...
- MT【32】内外圆(Apollonius Circle)的几何证明
另一方面,如果 M 满足(1)式,那么M必然在以PQ为直径的圆上.事实上当M为P或者Q时,这是显然的.当M异于P,Q时,由$\frac{|MB|}{|MC|}=\frac{|PB|}{|PC|}=\l ...
- MT【172】内外圆
$P,Q$是两个定点,M为平面内一个动点,且$\dfrac{|MP|}{|MQ|}=\lambda(\lambda>0,\lambda\ne1)$, 点M的轨迹围成的区域面积为S , 设$S=f ...
- MT【210】四点共圆+角平分线
(2018全国联赛解答最后一题)在平面直角坐标系$xOy$中,设$AB$是抛物线$y^2=4x$的过点$F(1,0)$的弦,$\Delta{AOB}$的外接圆交抛物线于点$P$(不同于点$A,O,B$ ...
- MT【306】圆与椭圆公切线段
已知椭圆方程$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$,圆方程$x^2+y^2=r^2,(3<r^2<4)$,若直线$l$与椭圆和圆分别切于点$P,Q$求$|PQ| ...
- MT【125】四点共圆
(2017湖南省高中数学竞赛16题) \(AB\)是椭圆\(mx^2+ny^2=1(m>0,n>0,m\ne n)\)的斜率为 1 的弦.\(AB\)的垂直平分线与椭圆交于两点\(CD\) ...
- MT【107】立体几何中用阿波罗尼乌斯圆的一道题
分析:利用内外圆知识知道,B,C两点到 AD 的距离$\le4$. 利用体积公式$V=\frac{1}{3}S_{截面}|AD|\le2\sqrt{15}$
- MT【191】阿波罗尼乌斯圆
已知$f(x)=2\sqrt{(\cos x+\frac{1}{2})^2+\sin^2 x}-\sqrt{\cos^2 x+(\sin x-\frac{1}{2})^2}$,若$m\ge f(x)$ ...
- C++ 2(将类分文件) //点和圆的关系 //设计一个圆形类 和一个点类 计算点和圆的关系 //点到圆心的距离 == 半径 点在圆上 //点到圆心的距离 > 半径 点在圆外 //点到圆心的距离 < 半径 点在圆内 //点到圆心的距离 获取 ....... (x1 -x2)^2 + (y1-y2)^2 开根号 和半径对比 // 计算 可以 两边同时 平方
1 源文件 main.cpp 2 //点和圆的关系 3 //设计一个圆形类 和一个点类 计算点和圆的关系 4 //点到圆心的距离 == 半径 点在圆上 5 //点到圆心的距离 > 半径 点在圆外 ...
随机推荐
- Python—反射
反射 1 什么是反射 反射的概念是由Smith在1982年首次提出的,主要是指程序可以访问.检测和修改它本身状态或行为的一种能力(自省).这一概念的提出很快引发了计算机科学领域关于应用反射性的研究.它 ...
- Factors of Factorial AtCoder - 2286 (N的阶乘的因子个数)(数论)
Problem Statement You are given an integer N. Find the number of the positive divisors of N!, modulo ...
- JS 获取链接中的参数
1.获取链接全部参数,以对象的形式返回 //获取url中参数 function GetRequest() { var url = location.search; //获取url中"?&qu ...
- java面试题2019
面向对象的特征有哪些方面? 原来学的时候说是三种特征,即封装.继承和多态. 现在一般说面向对象有四大特性,即抽象.封装.继承和多态. 1.抽象:将同类对象的共同特征提取出来构造类. 2.封装:将数据隐 ...
- MyEclipse 10.X激活方法
普遍的激活办法请参考: http://blog.csdn.net/miss_kun/article/details/51819206 http://jingyan.baidu.com/article/ ...
- 1 Expression of Possiblity
Expression of possibility Probably Perhaps There's a change(that) It's very likly(that) It's pos ...
- Ajax发送请求等待时弹出模态框等待提示
主要的代码分为两块,一个是CSS定义模态框,另一个是在Ajax中弹出模态框. 查看菜鸟教程中的模态框教程demo,http://www.runoob.com/try/try.php?filename= ...
- Day 5-8 自定义元类控制类的实例化行为
__call__方法: 对象后面加括号,触发执行. 注:构造方法的执行是由创建对象触发的,即:对象 = 类名() :而对于 __call__ 方法的执行是由对象后加括号触发的,即:对象() 或者 类( ...
- Python Note1: Pycharm的安装与使用
前言 曾经学过一段时间python,虽然现在工作了主要使用C#和C++,但是觉得还是有必要在业余的时候学习学习python,提升下自己的知识面,毕竟技多不压身,加油吧! 安装与激活Pycharm 个人 ...
- git上传本地代码到github
1.(先进入项目文件夹)通过命令 git init 把这个目录变成git可以管理的仓库 git init 2.把文件添加到版本库中,使用命令 git add .添加到暂存区里面去,不要忘记后面的小 ...
