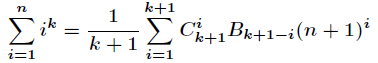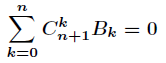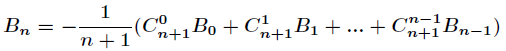51Nod - 1228 序列求和 (自然数幂和+伯努利数)
https://vjudge.net/problem/51Nod-1228
Description
T(n) = n^k,S(n) = T(1) + T(2) + ...... T(n)。给出n和k,求S(n)。
Input
第1行:一个数T,表示后面用作输入测试的数的数量。(1 <= T <= 5000)
第2 - T + 1行:每行2个数,N, K中间用空格分割。(1 <= N <= 10^18, 1 <= K <= 2000)Output共T行,对应S(n) Mod 1000000007的结果。
Sample Input
- 3
- 5 3
- 4 2
- 4 1
Sample Output
- 225
- 30
- 10
分析
求自然数的幂和,有一个基于伯努利数的公式。
于是线性处理出每一项,那么每个case就是线性求解了。
伯努利数怎么计算呢?
首先B0=1,然后有
将Bn提取出来,得到
这样就能递推伯努利数了。
- #include <iostream>
- #include <cstdio>
- #include <cstdlib>
- #include <cstring>
- #include <string>
- #include <algorithm>
- #include <cmath>
- #include <ctime>
- #include <vector>
- #include <queue>
- #include <map>
- #include <stack>
- #include <set>
- #include <bitset>
- using namespace std;
- typedef long long ll;
- typedef unsigned long long ull;
- #define ms(a, b) memset(a, b, sizeof(a))
- #define pb push_back
- #define mp make_pair
- #define pii pair<int, int>
- #define eps 0.0000000001
- #define IOS ios::sync_with_stdio(0);cin.tie(0);
- #define random(a, b) rand()*rand()%(b-a+1)+a
- #define pi acos(-1)
- const ll INF = 0x3f3f3f3f3f3f3f3fll;
- const int inf = 0x3f3f3f3f;
- const int maxn = + ;
- const int maxm = + ;
- const int mod = 1e9+;
- ll C[maxn][maxn],B[maxn],inv[maxn];
- inline ll add(ll a){
- if(a>=mod) a-=mod;
- return a;
- }
- void init(){
- C[][]=;
- for(int i=;i<maxn;i++){
- C[i][]=C[i][i]=;
- for(int j=;j<i;j++){
- C[i][j]=add(C[i-][j-]+C[i-][j]);
- }
- }
- inv[]=;
- for(int i=;i<maxn;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod; //线性递推逆元
- B[]=;
- for(int i=;i<maxn-;i++){
- B[i]=;
- for(int j=;j<i;j++){
- B[i]=add(B[i]+C[i+][j]*B[j]%mod);
- }
- B[i]=add(B[i]*(-inv[i+])%mod+mod);
- }
- }
- ll tmp[maxn];
- int main() {
- #ifdef LOCAL
- freopen("in.txt", "r", stdin);
- // freopen("output.txt", "w", stdout);
- #endif
- init();
- int T;
- scanf("%d",&T);
- while(T--){
- ll n,k;
- scanf("%lld%lld",&n,&k);
- n%=mod; //这里取个模比较好,求tmp时才不会爆
- tmp[]=;
- for(int i=;i<maxn;i++) tmp[i]=tmp[i-]*(n+)%mod;
- ll ans=;
- for(ll i=;i<=k+;i++){
- ans=add(ans+C[k+][i]*B[k+-i]%mod*tmp[i]%mod);
- }
- ans=ans*inv[k+]%mod;
- printf("%lld\n",ans);
- }
- return ;
- }
51Nod - 1228 序列求和 (自然数幂和+伯努利数)的更多相关文章
- 51nod 1228 序列求和(伯努利数)
1228 序列求和 题目来源: HackerRank 基准时间限制:3 秒 空间限制:131072 KB 分值: 160 难度:6级算法题 收藏 关注 T(n) = n^k,S(n) = T(1 ...
- 51Nod 1228 序列求和
T(n) = n^k,S(n) = T(1) + T(2) + ...... T(n).给出n和k,求S(n). 例如k = 2,n = 5,S(n) = 1^2 + 2^2 + 3^2 + 4^ ...
- 51Node1228序列求和 ——自然数幂和模板&&伯努利数
伯努利数法 伯努利数原本就是处理等幂和的问题,可以推出 $$ \sum_{i=1}^{n}i^k={1\over{k+1}}\sum_{i=1}^{k+1}C_{k+1}^i*B_{k+1-i}*(n ...
- 51nod1228 序列求和(自然数幂和)
与UVA766 Sum of powers类似,见http://www.cnblogs.com/IMGavin/p/5948824.html 由于结果对MOD取模,使用逆元 #include<c ...
- 51nod 1228 序列求和 ( 1^k+2^k+3^k+...+n^k )
C为组合数,B为伯努利数 具体推到过程略 参考博客:http://blog.csdn.net/acdreamers/article/details/38929067# (我的式子和博客中的不一样,不过 ...
- 自然数幂和&伯努利数(Bernoulli)
二项式定理求自然数幂和 由二项式定理展开得 \[ (n+1)^{k+1}-n^{k+1}=\binom {k+1}1n^k+\binom {k+1}2n^{k-1}+\cdots+\binom {k+ ...
- 51NOD 1258 序列求和 V4 [任意模数fft 多项式求逆元 伯努利数]
1258 序列求和 V4 题意:求\(S_m(n) = \sum_{i=1}^n i^m \mod 10^9+7\),多组数据,\(T \le 500, n \le 10^{18}, k \le 50 ...
- UVA766 Sum of powers(1到n的自然数幂和 伯努利数)
自然数幂和: (1) 伯努利数的递推式: B0 = 1 (要满足(1)式,求出Bn后将B1改为1 /2) 参考:https://en.wikipedia.org/wiki/Bernoulli_numb ...
- 51nod 1258 序列求和 V4
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1258 1258 序列求和 V4 基准时间限制:8 秒 空间限制:131 ...
随机推荐
- 使用tree命令导出文件夹/文件的目录树
前提:己安装扩展: 介绍: TREE [drive:][path] [/F] [/A] /F 显示每个文件夹中文件的名称.(带扩展名) /A 使用 ASCII 字符,而不使用扩展字符. t ...
- SPHINX 文档写作工具安装简要指南 - windows 版 - 基于python
此教程基于本地己安装好 PYTHON 并配置过全局变量:一定具备相应的基础再操作: 上传图片以免产生误导,以下为文字描述,按下列操作即可: 下载 get-pip.py脚本; python get-pi ...
- Add Zabbix Agent
添加第三方源进行安装CentOS/RHEL 7:# rpm -Uvh http://repo.zabbix.com/zabbix/2.2/rhel/7/x86_64/zabbix-release-2. ...
- [2017-8-02]Android Learning Day9
Layout动画效果 为布局添加简单的动画效果 public class MainActivity extends AppCompatActivity { @Override protected vo ...
- centos7安装mha4mysql
mysql搭建mha需要用的两个rpm包.(manager包和node包) 下载地址:https://download.csdn.net/download/dajdajdajdaj/10603389 ...
- centos7/rhel7下配置PXE+Kickstart自动安装linux系统
应用场景:临时安装一个系统或者批量安装linux系统,无需人工介入选择下一步,减少在安装系统上的时间浪费,提高工作效率. DHCP + TFTP + Syslinux + FTP + Kickstar ...
- 蓝桥杯 错误票据 (stringstream的使用)
题目链接:http://lx.lanqiao.cn/problem.page?gpid=T28 问题描述 某涉密单位下发了某种票据,并要在年终全部收回. 每张票据有唯一的ID号.全年所有票据的ID号是 ...
- 真机控件获取 app-inspector
1.安装app-inspector:npm install app-inspector -g 若是要卸载原有的:npm uninstall app-inspector -g np ...
- semantic ui框架学习笔记一
面包屑导航 面包屑导航经常用于多个栏目下的内容管理,是web页面里比较常用的组合.例如: <div class="ui breadcrumb"> <a class ...
- appium-基础搭建,适配,问题,优化,提速
搭建开发环境,导入testng/log4j/maven 1.配置jdk环境 2.安装appium,下载eclipse-adt,配置appium环境 github.com/getlantern/foru ...