非线性优化（高翔slam---第六讲 ）

1.线性最小二乘问题

2.非线性最小二乘问题

因为它非线性，所以df/dx有时候不好求，那么可以采用迭代法（有极值的话，那么它收敛，一步步逼近）：

这样求导问题就变成了递归逼近问题，那么增量△xk如何确定？

这里介绍三种方法：

（1）一阶和二阶梯度法

将目标函数在x附近进行泰勒展开：

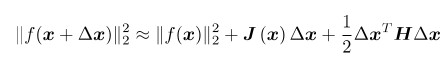
（2）高斯牛顿法

将f(x)一阶展开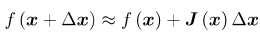：（1）

这里J(x)为f(x)关于x的导数，实际上是一个m×n的矩阵，也是一个雅克比矩阵。现在要求下降矢量△x，使得||f(x+△x)|| 达到最小。

为求△ x，我们需要解一个线性的最小二乘问题：

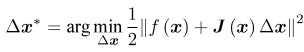
这里注意变量是△ x，而非之前的x。所以是线性函数，好求。为此，先展开目标函数的平方项：

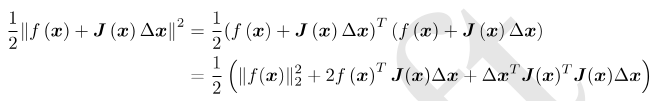
我们称为高斯牛顿方程。我们把左边的系数定义为H，右边定义为g，那么上式变为：

H △x=g

跟牛顿法对比可以发现，我们用J(x)^TJ(x)代替H的求法，从而节省了计算量。所以高斯牛顿法跟牛顿法相比的优点就在于此，步骤列于下：

但是，还是有缺陷，就是它要求我们所用的近似H矩阵是可逆的（而且是正定的），但实际数据中计算得到的J^TJ却只有半正定性。也就是说，在使用Gauss Newton方法时，可能出现J^TJ为奇异矩阵或者病态（ill-condition）的情况，此时增量的稳定性较差，导致算法不收敛。更严重的是，就算我们假设H非奇异也非病态，如果我们求出来的步长△x太大，也会导致我们采用的局部近似（1）不够准确，这样一来我们甚至都无法保证它的迭代收敛，哪怕是让目标函数变得更大都是可能的。

所以，接下来的Levenberg-Marquadt方法加入了α，在△x确定了之后又找到了α，从而||f(x+α△x)||²达到最小，而不是直接令α=1。

（3）列文伯格-马夸尔特方法（Levenberg-Marquadt法）

由于Gauss-Newton方法中采用的近似二阶泰勒展开只能在展开点附近有较好的近似效果，所以我们很自然地想到应该给△x添加一个信赖区域（Trust Region），不能让它太大而使得近似不准确。非线性优化中有一系列这类方法，这类方法也被称之为信赖区域方法（Trust Region Method）。在信赖区域里边，我们认为近似是有效的；出了这个区域，近似可能会出问题。

那么如何确定这个信赖区域的范围呢？

一个比较好的方法是根据我们的近似模型跟实际函数之间的差异来确定这个范围：如果差异小，我们就让范围尽可能大；如果差异大，我们就缩小这个近似范围。因此，考虑使用：来判断泰勒近似是否够好。ρ的分子是实际函数下降的值，分母是近似模型下降的值。如果ρ接近于1，则近似是好的。如果ρ太小，说明实际减小的值远少于近似减小的值，则认为近似比较差，需要缩小近似范围。反之，如果ρ比较大，则说明实际下降的比预计的更大，我们可以放大近似范围。

于是，我们构建一个改良版的非线性优化框架，该框架会比Gauss Newton有更好的效果。

1. 给定初始值x0，以及初始化半径μ。

2. 对于第k次迭代，求解：

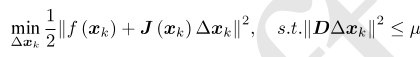（2）

这里面的限制条件μ是信赖区域的半径，D将在后文说明。

3. 计算ρ。

4. 若ρ>3/4，则μ=2μ；

5. 若ρ<1/4，则μ=0.5μ；

6. 如果ρ大于某阈值，认为近似可行。令xk+1=xk+△xk。

7. 判断算法是否收敛。如不收敛则返回2，否则结束。

这里近似扩大范围的倍数和阈值都是经验值，亦可替换成别的数值。在式（1）中，我们把增量范围限定在一个半径为μ的球中。带上D之后，这个球可以看成是个椭球。

（Levenberg提出的优化方法中，把D取成单位矩阵I，相当于直接把△x约束在球中。Marquart提出将D取成非负数对角阵---通常用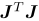的对角元素平方根。）

无论怎样，都需要解（2）这样一个问题来获得梯度，其是带不等式约束的优化问题，我们用Lagrange乘子将它转化为一个无约束优化问题：

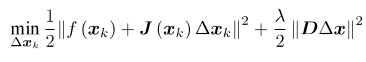
λ为Lagrange乘子。展开后，化简得到：

当λ比较小时，H占主要地位，接近于牛顿高斯法；当λ比较大时，接近于最速下降法。

L-M的求解方式，可在一定程度上避免线性方程组的系数矩阵的非奇异和病态问题，提供更稳定更准确的增量△x。

小结：

视觉SLAM里，这个矩阵往往有特定的稀疏形式，为实时求解优化问题提供了可能性。利用

稀疏形式的消元，分解，最后再求解增量，会让求解效率大大提高。（第十讲）

实践：

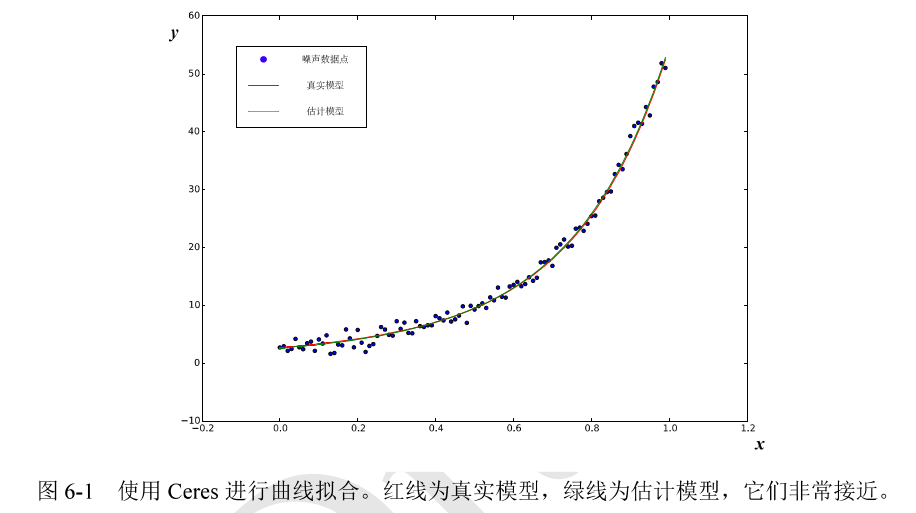
1.Ceres库(谷歌)

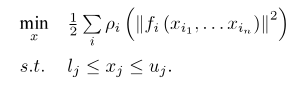
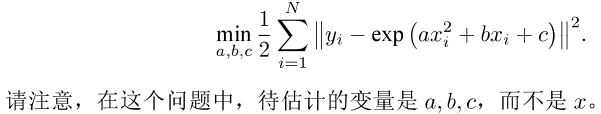
 2.g20库(基于图优化)

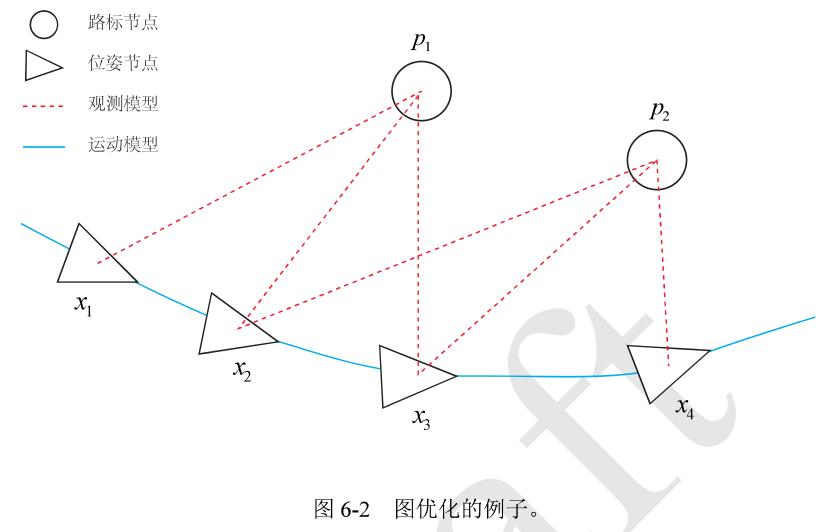
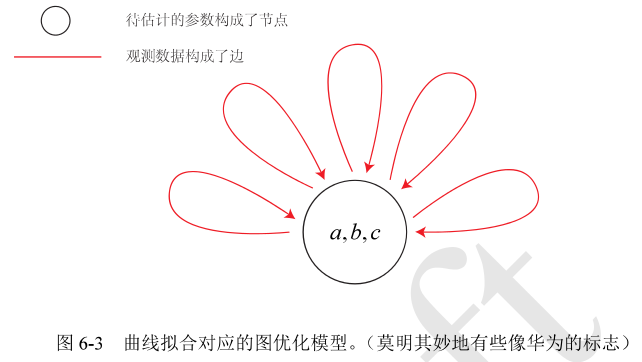
g20步骤：

总结：