Codeforces Round #493 (Div. 1)

A.

/*
发现每次反转或者消除都会减少一段0
当0只有一段时只能消除
这样判断一下就行

*/

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<set>
#include<map>
#define M 300010
#define ll long long

using namespace std;
int read() {
    int nm = , f = ;
    char c = getchar();
    for(; !isdigit(c); c = getchar()) if(c == '-') f = -;
    for(; isdigit(c); c = getchar()) nm = nm *  + c - '';
    return nm * f;
}
ll n,x,y;
char s[M];
int main() {
    n = read(), x = read(), y = read();
    scanf("%s", s + );
    int len = strlen(s + );
    s[] = '?';
    ll tot = ;
    for(int i = ; i <= len; i++) if(s[i] != s[i - ] && s[i] == '') tot++;
    if(tot == ) return puts("");
    cout << min(tot * y, tot * x - x + y);
    return ;
}

B.

/*
可能这种题是打表克星
小数据部分没有规律  数据大了有规律

//一个显然的结论 ，如果数字总数确定的话我们求 1， 5， 10， 50 加起来的不同和的个数相当于求0， 4， 9， 49 的
 好吧打打表就出来了
 对于前12的数据 直接暴力 ，后面的线性增加 

*/

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<set>
#include<map>
#define M 30
#define ll long long

using namespace std;
int read() {
    int nm = , f = ;
    char c = getchar();
    for(; !isdigit(c); c = getchar()) if(c == '-') f = -;
    for(; isdigit(c); c = getchar()) nm = nm *  + c - '';
    return nm * f;
}
const ll dx[]={,,,,,,,,,,,,,,,};
int main() {
    ll n = read();
    if(n <= ) cout << dx[n];
    else cout << dx[] + (n - ) * ;
    return ;
}

C.

显然同色的一行在哪一行对答案贡献是一样的，于是我们可以直接得出容斥的式子

/*
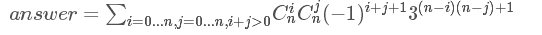
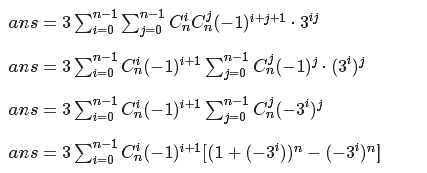
difficult 看题解啦

*/

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<set>
#include<map>
#define M 1231231
#define ll long long
const int mod = ;
using namespace std;
int read() {
    int nm = , f = ;
    char c = getchar();
    for(; !isdigit(c); c = getchar()) if(c == '-') f = -;
    for(; isdigit(c); c = getchar()) nm = nm *  + c - '';
    return nm * f;
}
ll poww(ll a, ll b) {
    ll as = , tmp = a;
    for(; b; b >>= , tmp = tmp * tmp % mod) if(b & ) as = as * tmp % mod;
    return as;
}
ll c[M];

inline ll ni(ll a) {
    return poww(a, mod - );
}
void shai(ll n) {
    c[] = ;
    for(int i = ; i <= n; i++) c[i] = c[i - ] * (n - i + ) % mod * ni(i) % mod;
}
int main() {
    ll n = read();
    ll ans = ;
    shai(n);
    for(int i = , j = ; i <= n; i++, j = -j) ans += j * c[i] % mod * poww(, (n - i) * n + i) % mod, ans %= mod;
    ans = ans *  % mod;
    for(int i = , j = -; i < n; i++, j = -j) ans += 3ll * c[i] * j % mod * (poww(1ll - poww(, i), n) - poww(-1ll * poww(3ll, i), n)) % mod, ans %= mod;
    cout << (ans + mod) % mod;
    return ;
}