Codeforces 528E Triangles 3000 - 计算几何

题目传送门

　　传送点I

　　传送点II

　　传送点III

题目大意

　　给定$n$的平面上的直线，保证没有三条直线共点，两条直线平行。问随机选出3条直线交成的三角形面积的期望。

　　显然$S=\frac{1}{2}ah$是不可用的。（压根感觉不可优化）

　　考虑向量的做法：$S = \frac{1}{2}(A \times B + B \times C + C\times A)$。（相当于把一个三角形拆成了三个以原点作为其中一个顶点的"有向"三角形）

　　于是考虑利用向量叉积对向量加法的分配律进行优化。

　　枚举第一条直线，剩下的直线按照极角序加入，不断计算交点和有向面积。

　　对于直线的方向，我是根据原点在直线的哪一侧决定的。（比如定向后，原点在它左侧）

　　然后画三条直线相交，讨论原点在哪，然后再讨论怎么计算有向面积。

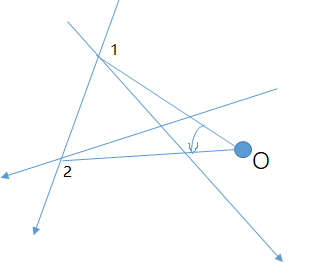
　　画一张图仅供参考，1和2表示是交点被计算的顺序。

　　开心地发现原点在三角形内部的时候计算叉积的时候需要取相反数计入答案。

　　这很烦。所以取一个超级远的地方的点作为原点就可以成功避开了这个问题。

Code

 /**
  * Codeforces
  * Problem#528E
  * Accepted
  * Time: 78ms
  * Memory: 100k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 //Comparison of floating point constants
 const double eps = 1e-;
 //π
 const double pi = acos((double)-);

 //Define the points and the vectors
 typedef class Point {
     public:
         double x;
         double y;
         Point(const double x = 0.0, const double y = 0.0):x(x), y(y) {        }
 }Point, Vector;

 const Point O(1e7, 1e7);

 Vector operator + (Vector a, Vector b) {
     return Vector(a.x + b.x, a.y + b.y);
 }

 Vector operator - (Vector a, Vector b) {
     return Vector(a.x - b.x, a.y - b.y);
 }

 Vector operator * (Vector a, double b) {
     return Vector(a.x * b, a.y * b);
 }

 Vector operator * (double b, Vector a) {
     return Vector(a.x * b, a.y * b);
 }

 Vector operator / (Vector a, double b) {
     return Vector(a.x / b, a.y / b);
 }

 Vector operator - (Vector a) {
     return Vector(-a.x, -a.y);
 }

 int dcmp(double x) {
     if(fabs(x) < eps)    return ;
     return (x < ) ? (-) : ();
 }

 double Dot(Vector a, Vector b) {
     return a.x * b.x + a.y * b.y;
 }

 double Cross(Vector a, Vector b) {
     return a.x * b.y - a.y * b.x;
 }

 double Area(Point a, Point b, Point c) {
     return fabs(Cross(b - a, c - a) / );
 }

 Point getLineIntersection(Point A, Vector v, Point B, Vector u) {
     Vector w = B - A;
     double t = (Cross(w, u) / Cross(v, u));
     return A + t * v;
 }

 typedef class Line {
     public:
         Point p;
         Vector v;
         double ang;
         int id;

         Line() {    }
         Line(int a, int b, int c, int id):id(id) {
             if (!b) {
                 p = Point(c * 1.0 / a, );
                 v = Point(, );
             } else {
                 p = Point(, c * 1.0 / b);
                 v = Point(-b, a);
             }
             if (Cross(O - p, v) > )
                 v = -v;
             ang = atan2(v.y, v.x);
         }

         boolean operator < (Line b) const {
             return ang < b.ang;
         }
 }Line;

 ostream& operator << (ostream& os, Point p) {
     os << "(" << p.x << " " << p.y << ")";
     return os;
 }

 int n;
 Line *ls;

 inline void init() {
     scanf("%d", &n);
     ls = new Line[(n + )];
     for (int i = , a, b, c; i <= n; i++) {
         scanf("%d%d%d", &a, &b, &c);
         ls[i] = Line(a, b, c, i);
     }
 }

 double res = 0.0;
 inline void solve() {
     sort(ls + , ls + n + );
 //    for (int i = 1; i <= n; i++)
 //        cerr << ls[i].p << " " << ls[i].v << " " << ls[i].ang << endl;
     for (int i = ; i <= n; i++) {
         Point sP(, ), P;
         for (int j = i + ; j <= n; j++) {
             P = getLineIntersection(ls[i].p, ls[i].v, ls[j].p, ls[j].v) - O;
 //            int d = dcmp(Cross(ls[i].v, ls[j].v));
             res += Cross(sP, P);
             sP = sP + P;
         }
         for (int j = ; j < i; j++) {
             P = getLineIntersection(ls[i].p, ls[i].v, ls[j].p, ls[j].v) - O;
 //            int d = dcmp(Cross(ls[i].v, ls[j].v));
             res += Cross(sP, P);
             sP = sP + P;
         }
     }
     printf("%.9lf", res *  / n / (n - ) / (n - ));
 }

 int main() {
     init();
     solve();
     return ;
 }