angular 2 - 002 - 基本概念和使用
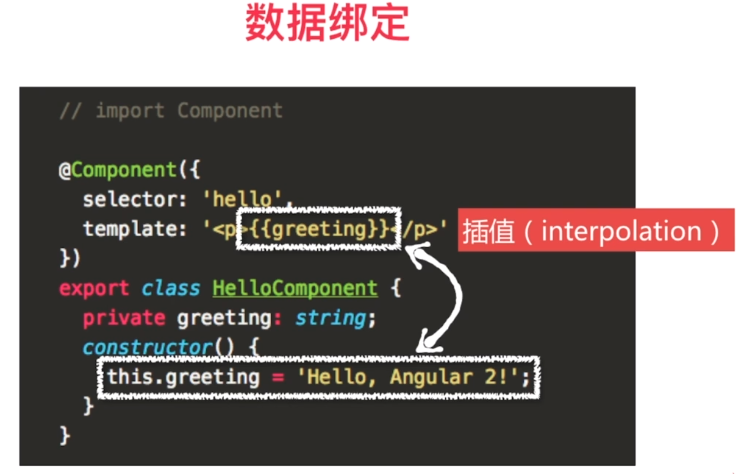

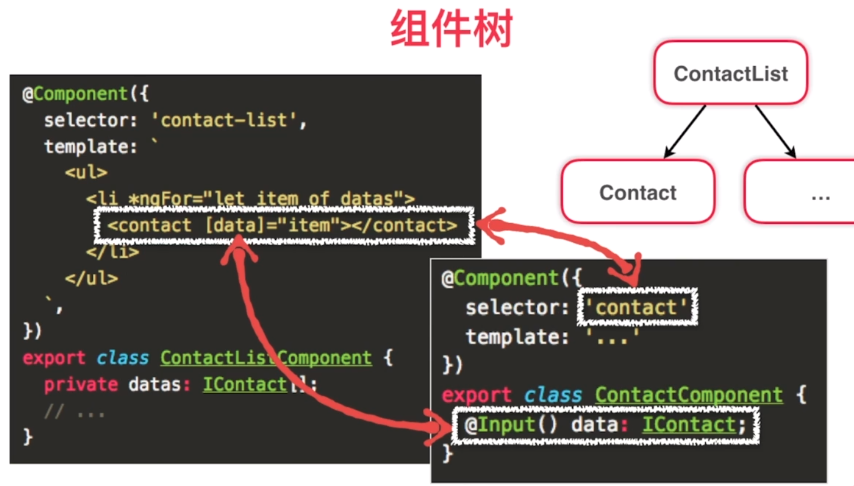
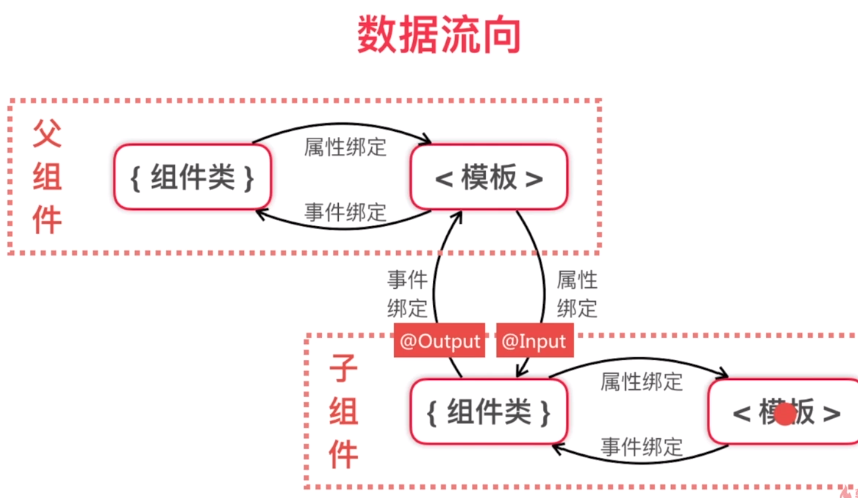
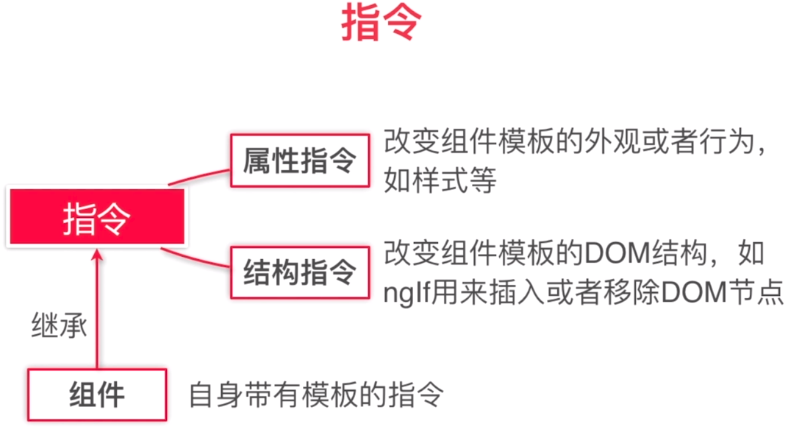



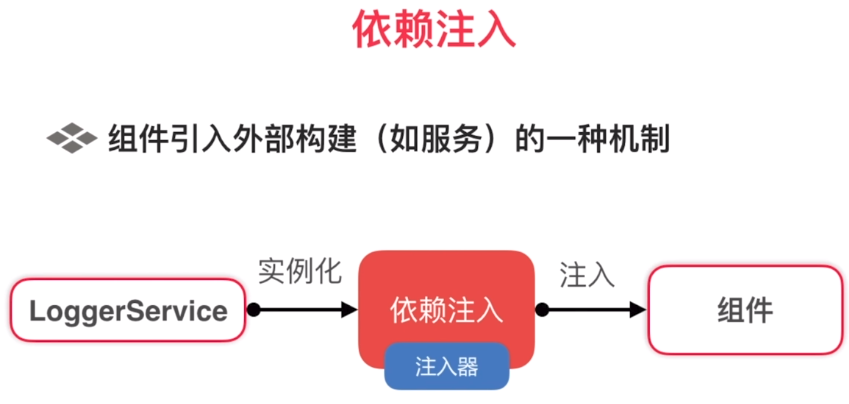
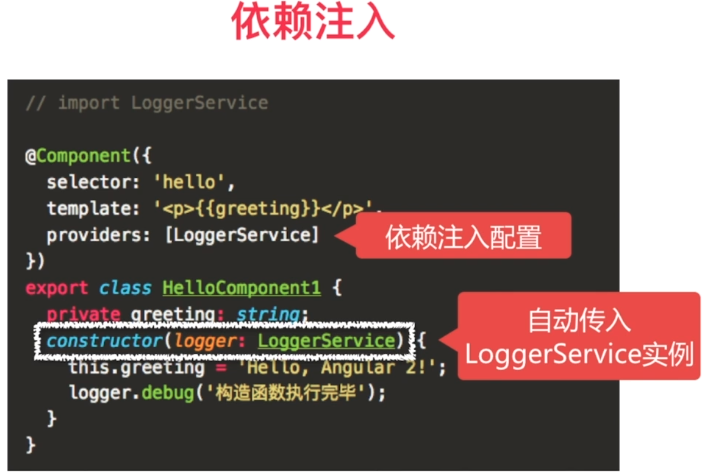
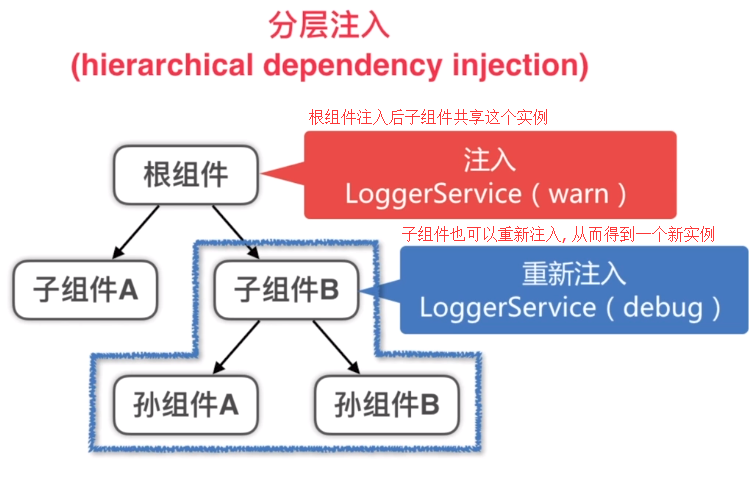
service的注入, 注入的是service的单一实例



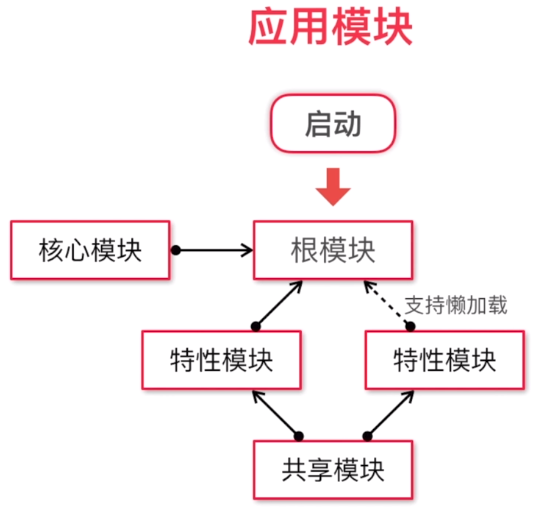
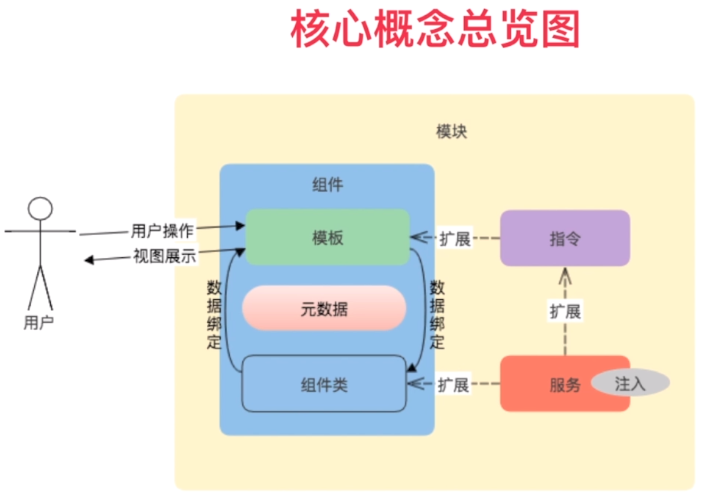
angular 2 - 002 - 基本概念和使用的更多相关文章
- 2 Angular 2 的核心概念
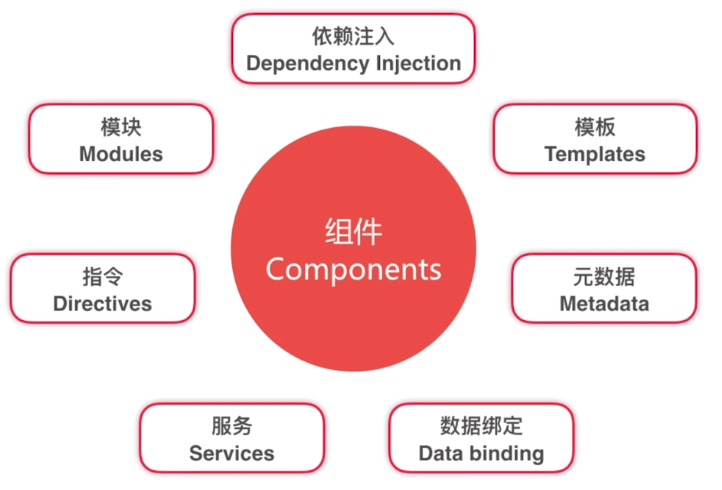
一.组件(Components): 组件是构成 Angular 应用的基础和核心,它是一个模板的控制类,用于处理应用和逻辑页面的视图部分.组件知道如何渲染自己及配置依赖注入,并通过一些由属性和方法组成 ...
- Angular作用域的层级概念(scope)
首先引入 angular 的根作用域:$rootScope ng-app:定义了angualr的作用域 ng-controller:定义了控制器 $scope定义了视图与控制器之间的纽带,而scope ...
- angular.js学习笔记--概念总结
好久没更新了,现在开始学习学习angularjs,并且把学习到的一些知识总结记录一下,方便以后查找以及希望能给初学者一些帮助!(由于本人也是初学ng所以各位慎重理解!) 废话不多说,开始! $root ...
- 实践总结 - 不可错过的Angular应用技巧
angular的核心思想是通过数据驱动一切,其他东西都是数据的延伸. 套用Javascript一切皆对象的思想,在angular中可以说一切皆数据. 关于项目构建 (1) requirejs以及Yeo ...
- Angular 1与 Angular 2之间的一些差别
现在在用ng1.5.8做一个项目,ng的优点和特性我就不用多说了,ng1在陆续更新到1.5/1.6后就没再推出新版本了,ng2已经面世测试很久了,如同很多系统和框架一样,每个大的版本更新都会有新特性加 ...
- 翻译:Angular 2 - TypeScript 5 分钟快速入门
原文地址:https://angular.io/docs/ts/latest/quickstart.html Angular 2 终于发布了 beta 版.这意味着正式版应该很快就要发布了. 让我们使 ...
- angular入门系列教程2
主题: 本篇主要介绍下angular里的一些概念,并且在咱们的小应用上加上点料.. 概念(大概了解即可,代码中遇到的会有详细注释): 模板:动态模板,是动态的,直接去处理DOM的,而不是通过处理字符串 ...
- TypeScript 5 Angular 2
TypeScript 5 分钟快速入门 翻译:Angular 2 - TypeScript 5 分钟快速入门 原文地址:https://angular.io/docs/ts/latest/quicks ...
- Angular 2的12个经典面试问题汇总(文末附带Angular测试)
Angular作为目前最为流行的前端框架,受到了前端开发者的普遍欢迎.不论是初学Angular的新手,还是有一定Angular开发经验的开发者,了解本文中的12个经典面试问题,都将会是一个深入了解和学 ...
随机推荐
- 给定两个字符串 s 和 t,它们只包含小写字母。 字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。 请找出在 t 中被添加的字母。
给定两个字符串 s 和 t,它们只包含小写字母.字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母.请找出在 t 中被添加的字母. 示例: 输入: s = "abcd" ...
- forward 和redirect
http://www.cnblogs.com/davidwang456/p/3998013.html
- VDOM总结
https://segmentfault.com/a/1190000016129036
- webpack的总结
1,首先 项目的入口----package的入口 "scripts": { "dev": "node build/dev-server.js" ...
- Web界面实现数据库增删改查过程
实现方法:JSP+Servlet+JavaBean 基本实现思想:jsp文件为显示界面,包括增删改查四个界面,然后使用form或者href超链接的方法将网页获得的值传到Servlet中的方法里:而se ...
- poj1041 【无向图欧拉回路】 按最小升序输出
题目链接:http://poj.org/problem?id=1041 题目大意: 题目大意:一个城镇有n个二叉路口,这些路口由m条街道连接,某人想要从某个路口出发,经过所有的街道且每条街道只走一次, ...
- Pedestrian Attributes Recognition Paper List
Pedestrian Attributes Recognition Paper List 2018-12-22 22:08:55 [Note] you may also check the upda ...
- docker+springboot+elasticsearch+kibana+elasticsearch-head整合(详细说明 ,看这一篇就够了)
一开始是没有打算写这一篇博客的,但是看见好多朋友问关于elasticsearch的坑,决定还是写一份详细的安装说明与简单的测试demo,只要大家跟着我的步骤一步步来,100%是可以测试成功的. 一. ...
- Socket 网络通信
Socket 网络通信 1.OSI (Open System Interconnect Reference Model)(开放系统互联参考模型) 从下低到高 :物理层.数据链路层.网络层.传输层.会话 ...
- 橡皮筋进度条ElasticProgressBar
橡皮筋进度条ElasticProgressBar 橡皮筋进度条是一个极具动画效果的进度条.该进度条不仅具有皮筋效果,还带有进度数据显示,让用户可以很清晰的看到当前的进度,可用于下载.加载进度等场景.E ...
