椭圆曲线签名算法的v的定义

在之前的个个与签名相关的地方我都对v的定义感到十分困惑，知道查看了黄皮书以后才对它的作用有了一定地了解，如下：

(v is the recovery id: a 1 byte value specifying the sign and finiteness of the curve point; this value is in the range of [27, 30], however the Ethereum protocol declares the upper two possibilities, representing infinite values, invalid)

v是恢复id: 1字节值，指定曲线点的符号和有限性.这个值在[27,30]的范围内，但是Ethereum协议声明了上面的两种可能性，表示无限的值，无效

查看黄皮书可见：

specify the parity and finitness of the coordinates of curve point for which r is the x-value

指定r为x值(s为y值)的曲线点坐标的奇偶性和有限度，因为当r值确定时，在椭圆曲线上是有两个点的，v是用于说明那个点才是真正符合结果的点

r为点的x坐标，s为点的y坐标，v坐标的奇偶检验标识符，27表示偶数y, 28表示奇数y

the value is in the range of [27,30],however we declare the upper two possibilities,representing infinite values,invalid

这个值在[27,30]的范围内，但是我们声明上面两种表示无限值的可能性无效(即只有当r,s代表的点是有限的时，v才是有效的)

v用做奇偶校验，27表示偶数y, 28表示奇数y。

当发生分叉后，the message hash有两种，一种是没分叉时当v 为{27,28}时，只hash前六个元素，而是（nonce, gasprice, startgas, to, value, data)；另一种是分叉后hash九个元素（还要再加上CHAIN_ID,r=0,s=0）

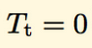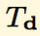而且，如果，则说明to address = 0x0,那么p = ,即input；不然就为，即data

签名后得到的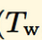（即v）有两种值的可能，当其作为标识符时，它的结果为{27,28};但是如果它与分叉chainId有关时，它的值为 chainId*2 =35 或chainId *2 +36，它也能表示y的奇偶性，作为奇偶检验，35表示偶数y, 36表示奇数y

当复原recover时，v也会根据上面的两种可能来进行变化，如果是与chainId有关，则在输入recover函数前，要先使用 来进行转换

在不同的客户端可见返回的值也有所不同：

In Geth, v is always 00 or 01. In testrpc, v is always 1a (27) or 1b (28).