洛谷P2900 [USACO08MAR]土地征用Land Acquisition（动态规划，斜率优化，决策单调性，线性规划，单调队列）

洛谷题目传送门

用两种不一样的思路立体地理解斜率优化，你值得拥有。

题意分析

既然所有的土地都要买，那么我们可以考虑到，如果一块土地的宽和高（其实是蒟蒻把长方形立在了平面上）都比另一块要小，那么肯定是直接并购，这一块对答案没有任何贡献。

我们先把这些给去掉，具体做法可以是，按高为第一关键字，宽为第二关键字从大到小排序，然后上双指针扫一遍。

于是，剩下的就是一个高度递减、宽度递增的矩形序列。考虑怎样制定它们的并购方案会最优。显然如果要并购，一定要挑序列中的一段区间，这样贡献答案的就只有最左边矩形的高乘上最右边矩形的宽，中间的又是没有贡献了。

设\(f_i\)为前\(i\)个矩形的最小花费，\(w\)为宽，\(h\)为高，直接写出一个\(O(n^2)\)的方程

\[f_i=\min\limits_{j=1}^i\{f_{j-1}+w_ih_j\}
\]

一看貌似是一个决策单调性优化的式子。然而。。。。。。

初中生都会的函数图像法

这种理解方法是在决策单调性优化DP的基础上应运而生的。

或者说，（在大多数情况下）斜率优化可以看作决策单调性优化的一种特殊情形。蒟蒻建议还是先入手决策单调性再来斜率优化吧。

蒟蒻的DP各种优化总结

蒟蒻之前写的一道经典（裸）决策单调性题的题解戳这里（Lightning Conductor）

对于每一个\(f_{j-1}+w_ih_j\)，我们都可以把它视为一个直线\(l_j:y=ax+b\)，其中\(a=h_j,b=f_{j-1}\)。对于每一个\(i\)，我们就是需要求出所有\(j\le i\)的直线的\(x\)取\(w_i\)时最小的一个\(y\)值。仍然用KmPlot画一个我们需要维护的所有直线的样子，它们应该满足斜率依次递减。

\(l_1:y=2x;\)

\(l_2:y=x+1;\)

\(l_3:y=\frac x 2+3;\)

\(l_4:y=\frac x 6+5.\)

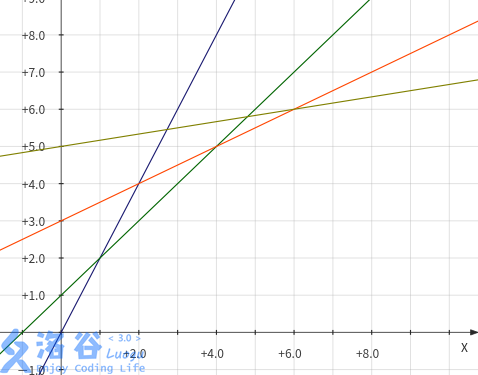
真正有用的部分

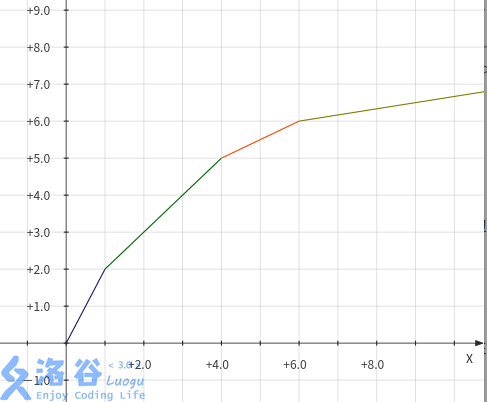
这样的话，我们就用单调队列维护若干个斜率递减的函数。我们仍然需要按照决策单调性的做法，维护相邻两个决策直线间的临界值（交点）\(k\)。难道还要维护决策二分栈，对每个临界值都二分么？

这些决策不是直线吗？求两个直线的交点。。。。。。初中数学就教了，是\(O(1)\)的。也就是对两个相邻决策直线\(l_1,l_2\)，我们求\(\frac{b_2-b_1}{a_1-a_2}\)。其它过程跟决策单调性是一模一样的。直线入队前，如果队尾不满足斜率递增则出队。求\(f_i\)之前，先把队首临界值\(\le w_i\)的决策出队，那么现在队首就是最优决策了。

这样求出\(f_n\)只需要\(O(n)\)的时间。

高中生都会的线性规划法

这才是理解斜率优化的正宗方法，因为上面并没有充分体现对斜率的处理过程。

上面对两个相邻直线求\(\frac{b_2-b_1}{a_1-a_2}\)，看起来有点像求什么东西。

我们原来把决策当成直线，斜率为\(a\)，截距为\(b\)。现在我们换一下。把决策\(f_{j-1}+w_ih_j\)看作一个点\(p_j(x,y)\)，其中\(x=-h_j,y=f_{j-1}\)。

现在要求解的问题又变成了什么样子呢？在平面上有若干个点，把\(f_i\)看成目标函数\(z\)，我们需要找到\(f_i=w_ih_j+f_{j-1}\)即\(z=-w_ix+y\)的最小值。这不是个线性规划么？

把式子变成\(y=w_ix+f_i\)，现在就让我们来最小化截距\(f_i\)。手(nao)动(dong)模拟一下，我们现在正在拿着一个斜率为\(w_i\)的直线，从下往上移动，当第一次经过某个决策点的时候，直线的在\(y\)轴上的截距就是我们要求的目标函数\(f_i\)的最小值了。

随便画一堆点就可以发现，无论直线以怎样的斜率向上靠，总有一些点永远都不会第一次与直线相交，也就是说这些决策是没用的。剩下的有用的决策点会构成一个凸包：（因为要画点所以换成了GeoGebra）

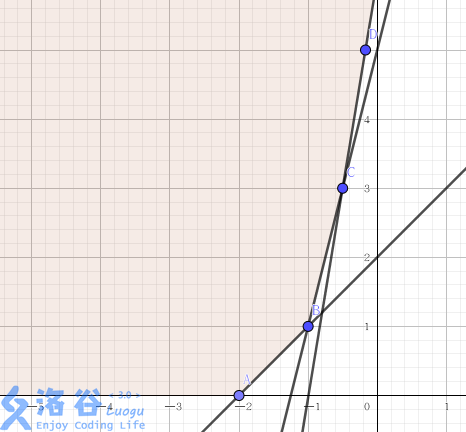
凸包的性质就是斜率递增/递减。在此题中，因为\(w\)递增，所以我们的单调队列中存的是若干个点满足\(x\)递增（\(h\)递减），\(y\)递增，而且相邻两个点的斜率也递增。这和原序列的顺序是同向的。假设队尾下标为\(t\)，当需要在队尾加入一个新的决策点时，我们可能会遇到这样的情况：

这时候\(p_t\)已经不优了，我们把它出队，如此直到满足斜率递增为止，\(p_i\)就可以入队了。和上面那种理解方法的写法差不多，求相邻两个点形成的直线斜率然后比一下大小。队首的处理跟上面那种理解方法的写法也差不多，如果队首与后一个的斜率小于\(w_i\)就出队。最后的队首依然是最优解。

实现

两种实现的代码长得都差不多，都要搞一个单调队列，都要求临界值/斜率。所以就放一个代码吧。。。

复杂度\(O(n\log n)\)，瓶颈竟然在sort上？！蒟蒻可不想来什么wys排序

#include<cstdio>
#include<algorithm>
#define RG register
#define R RG int
#define G c=getchar()
#define Calc(i,j) (f[j-1]-f[i-1])/(a[i].h-a[j].h)
//method1:求出临界值
//method2:求出斜率
using namespace std;
const int N=1e5+9;
int q[N];
double f[N],k[N];
//method1:k_i为决策直线q_i与q_i+1的临界值（交点）
//method2:k_i为决策点q_i与q_i+1所连成直线的斜率
struct Land{
	int w,h;//结构体排序
	inline bool operator<(RG Land&x)const{
		return h>x.h||(h==x.h&&w>x.w);
	}
}a[N];
inline int in(){
	RG char G;
	while(c<'-')G;
	R x=c&15;G;
	while(c>'-')x=x*10+(c&15),G;
	return x;
}
int main(){
	R n=in(),i,h,t;
	for(i=1;i<=n;++i)
		a[i].w=in(),a[i].h=in();
	sort(a+1,a+n+1);
	for(h=i=1;i<=n;++i)//双指针扫描去除无用矩形
		if(a[h].w<a[i].w)a[++h]=a[i];
	n=h;
	for(h=i=1,t=0;i<=n;++i){
		while(h<t&&k[t-1]>=Calc(q[t],i))--t;//维护临界值/斜率单调
		k[t]=Calc(q[t],i);q[++t]=i;//加入决策直线/决策点
		while(h<t&&k[h]<=a[i].w)++h;//弹出已经不优的决策
		f[i]=(double)a[q[h]].h*a[i].w+f[q[h]-1];//求出最优解
	}
	printf("%.0lf\n",f[n]);
	return 0;
}