问题:如何快速把$cos^4xsin^3x$表示成正弦，余弦的线性组合？

分析:利用牛顿二项式展开以下表达式:

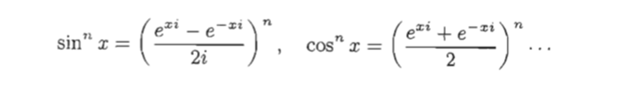
再利用欧拉公式$e^{i\theta}=cos\theta+isin\theta$

比如：

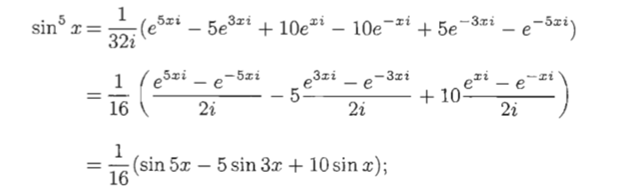
解答:

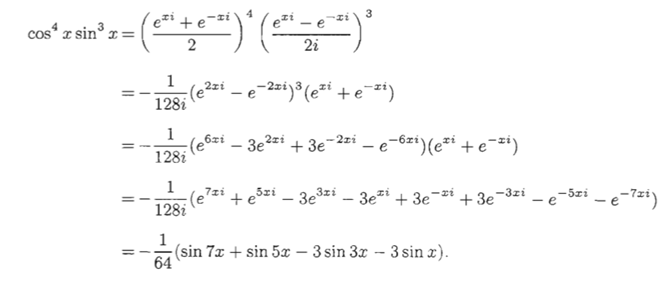
评:这样的变换,表示成线性组合在求积分的时候就显得很有用,大学自主招生迟早会考察以上变换。

MT【34】正余弦的正整数幂次快速表示成正余弦的线性组合的更多相关文章

  1. FZU-1752.(A^B mod C)(快速幂与快速乘优化)

    我把自己演哭了... 心酸.jpg 写了很多个版本的,包括数学公式暴力,快速幂TLE等等,最后想到了优化快速幂里的乘法,因为会爆longlong,但是和别人优化的效率简直是千差万别...? 本题大意: ...

  2. 矩阵乘法&矩阵快速幂&矩阵快速幂解决线性递推式

    矩阵乘法,顾名思义矩阵与矩阵相乘, 两矩阵可相乘的前提:第一个矩阵的行与第二个矩阵的列相等 相乘原则: a b     *     A B   =   a*A+b*C  a*c+b*D c d     ...

  3. 尾数为0零BigDecimal不能装成正常数

    BigDecimal b1 = rs.getBigDecimal("binary_double_column"); System.out.println( "ceshi: ...

  4. 快速幂 ，快速幂优化，矩形快速幂（java）

    快速幂形式 public static int f(int a,int b,int c){ int ans =1; int base=a; while(b!=0){ if((b&1)!=0) ...

  5. 求幂大法，矩阵快速幂，快速幂模板题--hdu4549

    hdu-4549 求幂大法.矩阵快速幂.快速幂 题目 M斐波那契数列 Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 ...

  6. JS 提交反斜杠\替换成正斜杠/

    js将字符串中所有反斜杠\替换成正斜杠/ 区分正斜杠与反斜杠: 正斜杠:http://.http紧跟着的斜杠,离手输入最近的斜杠,shift中间斜杠.45度角斜杠.正斜杠不需要转义 反斜杠:回车与空格 ...

  7. 整数快速乘法/快速幂+矩阵快速幂+Strassen算法

    快速幂算法可以说是ACM一类竞赛中必不可少,并且也是非常基础的一类算法,鉴于我一直学的比较零散,所以今天用这个帖子总结一下 快速乘法通常有两类应用:一.整数的运算,计算(a*b) mod c  二.矩 ...

  8. 快速幂 & 矩阵快速幂

    目录 快速幂 实数快速幂 矩阵快速幂 快速幂 实数快速幂 普通求幂的方法为 O(n) .在一些要求比较严格的题目上很有可能会超时.所以下面来介绍一下快速幂. 快速幂的思想其实是将数分解,即a^b可以分 ...

  9. GPU编程shader之正余弦波和幂/指数函数

    先上一个demo代码: <!DOCTYPE html> <html lang="en"> <head> <meta charset=&qu ...

随机推荐

  1. CF293B Distinct Paths 搜索

    传送门 首先数据范围很假 当\(N + M - 1 > K\)的时候就无解 所以对于所有要计算的情况,\(N + M \leq 11\) 超级小是吧,考虑搜索 对于每一个格子试填一个数 对于任意 ...

  2. Ubuntu 16.04 下部署Node.js+MySQL微信小程序商城

    转载于这篇文章 关于pm2看这篇文章 最近在研究小程序,申请了域名之后,再一次来配置环境,根据作者的步骤基本上完成了网站的架构,但由于环境路径等不同,配置上会有所不同,因此记录下来. 1.更新系统和安 ...

  3. iisapp -a命令出现 :此脚本不能与WScript工作

    今天一个同事向我反馈,使用iis的命令时出现了如标题的问题. 通过百度,找到如下信息: iisapp实际上是存放在C:\windows \system32目录下的一个VBS脚本,全名为iisapp.v ...

  4. 《Head First 设计模式》例子的C++实现（1 策略模式）

    最近在学习设计模式,用的是 <Head First 设计模式>这本书.感觉这本书写的还是很不错的,深入浅出的介绍了各种常用的设计模式.唯一有点不方便的地方是这本书的例子全都是用的 Java ...

  5. 校内模拟赛 旅行(by NiroBC)

    题意: n个点的无向图,Q次操作,每次操作可以连接增加一条边,询问两个点之间有多少条边是必经之路.如果不连通,输出-1. 分析: 首先并查集维护连通性,每次加入一条边后,如果这条边将会连接两个联通块, ...

  6. HNOI2019 多边形 polygon

    HNOI2019 多边形 polygon https://www.luogu.org/problemnew/show/P5288 这题镪啊... 首先堆结论: 显然终止状态一定是所有边都连向n了 根据 ...

  7. WPF 矩形框8个控制点伸缩及拖拽

    最近在研发图片控件矩形框8个控制点进行控制边框的大小.位置等信息,之前查阅了相关的信息,比如别人整合的类:ControlResizer 这个类虽然是好,但是很大程度上是有限制,换句话说,它需要你二次更 ...

  8. Mysql优化系列（1）--Innodb重要参数优化

    1.简单介绍InnoDB给MySQL提供了具有提交,回滚和崩溃恢复能力的事务安全(ACID兼容)存储引擎.InnoDB锁定在行级并且也在SELECT语句提供一个Oracle风格一致的非锁定读.这些特色 ...

  9. Week 3 结对编程

    Group: 杜正远 潘礼鹏 结对编程: 优点: 集体荣誉感.你们已经是一个集体了,一定得为对方着想负责. 1.看对方的代码,彼此会互相学习到一些奇妙的方法. 2.结对编程能把两个事情分开,降低复杂度 ...

  10. logstash 解析日志文件

    input { file { path => "/usr/local/test/log.log" } } filter { grok { match => { &quo ...