BZOJ3545&3551[ONTAK2010]Peaks——kruskal重构树+主席树+dfs序+树上倍增

题目描述

在Bytemountains有N座山峰，每座山峰有他的高度h_i。有些山峰之间有双向道路相连，共M条路径，每条路径有一个困难值，这个值越大表示越难走，现在有Q组询问，每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰，如果无解输出-1。

输入

第一行三个数N，M，Q。
第二行N个数，第i个数为h_i
接下来M行，每行3个数a b c，表示从a到b有一条困难值为c的双向路径。
接下来Q行，每行三个数v x k，表示一组询问。

输出

对于每组询问，输出一个整数表示答案.(3551强制在线)

样例输入

10 11 4
1 2 3 4 5 6 7 8 9 10
1 4 4
2 5 3
9 8 2
7 8 10
7 1 4
6 7 1
6 4 8
2 1 5
10 8 10
3 4 7
3 4 6
1 5 2
1 5 6
1 5 8
8 9 2

样例输出

6
1
-1
8

【数据范围】

N<=10^5, M,Q<=5*10^5，h_i,c,x<=10^9。

　　题意要求找出所有与一个点u路径上最大边权小于等于x的点中点权第k大。在这里先介绍一个东西叫做kruskal重构树，kruskal重构树就是将kruskal得到的最小生成树按边权从小到大进行重构，对于一条边a——b边权为c，先建一个新节点x，点权为c，然后把a,b在重构树中所在子树的根节点分别连到x的下面，作为x的左右子树，最后将所有最小生成树的边都重构完之后所得到的树就是kruskal重构树。例如样例所建的重构树如下图所示，其中黑色点为原最小生成树的点，红色点为原最小生成树的边在重构树中对应的点，黑色点内数是原树点的编号，红色点内数是原树对应边边权。

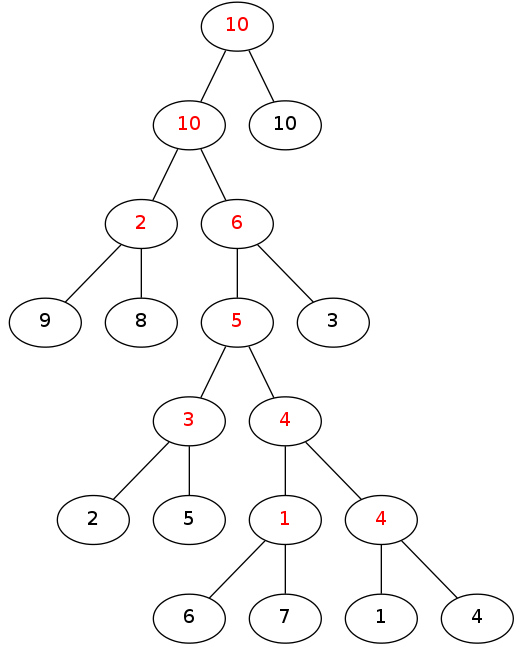
kruskal重构树有几个性质：

1、这是一棵二叉树且也是一个大根堆。

2、任意两个叶子节点在原树中路径上最大边权值为这两个点在重构树上lca的点权。

3、原树两点间路径边权最大值等于重构树中两点间路径点权最大值。

4、任意一个非叶子节点的子树中所有的叶子节点中，任意两个节点在原树中路径上边权最大值小于等于这个非叶子节点的点权(本题的关键)。

按dfs序把所有重构树上叶子节点排序，对于每次询问在重构树上倍增找到小于等于x的深度最浅的点a，利用主席树在a点子树所在dfs序的那段区间上求第k大的点就行了。注意题中没说明整张图联通。

最后附上代码(强制在线)。

#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mid (L+R)/2
using namespace std;
int cnt;
int tot;
int num;
int top;
int ans;
int x,y,z;
int n,m,k;
int a[200010];
int d[200010];
int b[200010];
int q[200010];
int g[200010];
int s[200010];
int t[200010];
int v[200010];
int h[200010];
int to[800010];
int l[6000010];
int r[6000010];
int vis[200010];
int head[200010];
int next[800010];
int sum[6000010];
int root[200010];
int f[200010][20];
struct edge
{
    int x;
    int y;
    int z;
}e[1000010];
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int find(int x)
{
    if(g[x]==x)
    {
        return x;
    }
    return g[x]=find(g[x]);
}
int ST(int x,int y)
{
    for(int i=19;i>=0;i--)
    {
        if(d[x]>=b[i]&&v[f[x][i]]<=y)
        {
            x=f[x][i];
        }
    }
    return x;
}
void add(int x,int y)
{
    tot++;
    next[tot]=head[x];
    head[x]=tot;
    to[tot]=y;
}
bool cmp(edge a,edge b)
{
    return a.z<b.z;
}
void dfs(int x)
{
    vis[x]=1;
    if(x<=n)
    {
        top++;
        q[top]=x;
    }
    else
    {
        s[x]=top;
    }
    for(int i=1;i<=19;i++)
    {
        if(d[x]>=b[i])
        {
            f[x][i]=f[f[x][i-1]][i-1];
        }
        else
        {
            break;
        }
    }
    for(int i=head[x];i;i=next[i])
    {
        d[to[i]]=d[x]+1;
        f[to[i]][0]=x;
        dfs(to[i]);
    }
    if(x>n)
    {
        t[x]=top;
    }
}
int build(int L,int R)
{
    int rt=++cnt;
    sum[rt]=0;
    if(L<R)
    {
        l[rt]=build(L,mid);
        r[rt]=build(mid+1,R);
    }
    return rt;
}
int updata(int pre,int L,int R,int x)
{
    int rt=++cnt;
    l[rt]=l[pre];
    r[rt]=r[pre];
    sum[rt]=sum[pre]+1;
    if(L<R)
    {
        if(x<=mid)
        {
            l[rt]=updata(l[pre],L,mid,x);
        }
        else
        {
            r[rt]=updata(r[pre],mid+1,R,x);
        }
    }
    return rt;
}
int query(int ll,int rr,int L,int R,int k)
{
    if(L>=R)
    {
        return L;
    }
    int x=sum[l[rr]]-sum[l[ll]];
    if(x>=k)
    {
        return query(l[ll],l[rr],L,mid,k);
    }
    else
    {
        return query(r[ll],r[rr],mid+1,R,k-x);
    }
}
int main()
{
    b[0]=1;
    for(int i=1;i<=19;i++)
    {
        b[i]=b[i-1]<<1;
    }
    n=read();
    m=read();
    k=read();
    for(int i=1;i<=n;i++)
    {
        a[i]=read();
        h[i]=a[i];
    }
    sort(h+1,h+1+n);
    for(int i=1;i<=n;i++)
    {
        a[i]=lower_bound(h+1,h+n+1,a[i])-h;
    }
    for(int i=1;i<=2*n;i++)
    {
        g[i]=i;
    }
    for(int i=1;i<=m;i++)
    {
        e[i].x=read();
        e[i].y=read();
        e[i].z=read();
    }
    num=n;
    sort(e+1,e+m+1,cmp);
    for(int i=1;i<=m;i++)
    {
        int fx=find(e[i].x);
        int fy=find(e[i].y);
        if(fx!=fy)
        {
            num++;
            g[fx]=g[fy]=num;
            v[num]=e[i].z;
            add(num,fx);
            add(num,fy);
            if(num==2*n-1)
            {
                break;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!vis[i])
        {
            dfs(find(i));
        }
    }
    root[0]=build(1,n);
    for(int i=1;i<=top;i++)
    {
        root[i]=updata(root[i-1],1,n,a[q[i]]);
    }
    while(k--)
    {
        x=read();
        y=read();
        z=read();
        if(ans!=-1)
        {
            x^=ans;
            y^=ans;
            z^=ans;
        }
        int j=ST(x,y);
        int adc=root[s[j]];
        int apc=root[t[j]];
        if(sum[apc]-sum[adc]<z)
        {
            ans=-1;
        }
        else
        {
            ans=h[query(adc,apc,1,n,sum[apc]-sum[adc]-z+1)];
        }
        printf("%d\n",ans);
    }
}