Fibonacci数列时间复杂度之美妙

Fibonacci数列:　　fib(0)=1　　fib(1)=1　　fib(n)=fib(n-1)+fib(n-2)

上课老师出了一道题，求下列函数的时间复杂度：

int fib(int d)
{
 
　　if (d==)
　　　　return ;
　　if (d==)
　　　　return ;
　　return fib(d-)+fib(d-);
}

老师是这样求的：

点的数目大约为满(完全)二叉树结点数目的一半，所以时间复杂度为O(2^n)。

但其实并不是这样！

严谨上说，并不能证明出点的数目是x^n层面的，我们也可以认为点的数目为nlogn级别，对吧?

从图上看，树的最低高度为n/2+1，只能说明点的数目至少为2^(n/2+1)而已。。。

fib(d)的计算步数为fib(d-1)的计算步数再加上fib(d-2)的计算步数，

fib(d)终究是由若干个f(0)和f(1)组成，设由x个f(0)和y个f(1)组成，表示成(x,y)，则：

fib(0): (1,0)　　fib(1):(0,1)　　fib(2):(1,1)　　fib(3):(1,2)　　……　　fib(n):(fib(n-2),fib(n-1))

fib(n)的总操作步数为fib(n-2)+fib(n-1)=fib(n)=，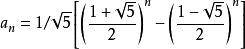

而(1-sqrt(5))/2相比(1+sqrt(5))/2较小，可以忽略不计，所有其时间复杂度为1 / sqrt(5) * [(1+sqrt(5))/2]^n。