SPH算法（求最小代价树）

一、sph算法简介

---

1.最小代价树算法

SPH算法也叫做MPH( minimum path heuristic)算法， 用于构造时延约束最算法小代价组播树. 该算法中每 个目的结点通过与当前组播树有最小代价的路径加入组播树，直到所有的目的节点全的进入树。

最小代价树算法中最经典的算法有 3 个: KMB 算法、ADH 算法、 MPH 算法.

• KMB 算法是由 Kou 等人提出的求解 Steiner 组播树算法, 其复杂度为 O(mn2);
• ADH ( average distance heuristic)算法复杂度为 O( n3);
• MPH 算法复杂度为 O( mn2).

---

2.MPH算法过程

到目前为 止,从降低组播生成树的代价方面考虑,MPH 仍是 一个非常优秀 的求解 Steiner 树问题 的启发式 算法. MPH 算法基本思想如下:

• 1. 初始化组播树 T,开始时只包括源结点 s;
• 1. 从余下的目的结点中选取到树 T 具有最小 代价路径的目的结点,将该结点及其最小代价路径 加入树 T ;
• 1. 重复 2) ,直到所有目的结点加入组播树 T

---

3.SPH算法过程

具体包括如下几个 步骤:

• 1)运用 Dijkstra算法,以点集S（初值为源点first）计算到所有结点的最小代价路径 ；
• 2)选出目的节点中间的代价最小的minNodes；
• 3)将到点minNodes的路径上的全部节点压进点集S；
• 4)重复1）、2）、3）直到所有的目标点集进入点集S；

其中Dijkstra算法是一个常用的解单源最短路径的常用算法。其基本思想是，设置一个顶点集合H，并不断贪心的选择来扩充这个集合。此算法网上描述很多，不进行赘述。

本次，完成Dijkstra后同时记录下最短路径的值及最短路径经过的节点，数据结构也只是用了比较low的表去实现。

第二步中间选取最小的minNodes时，下一步的优化方向是采用最小优先级对列的数据结构，及堆算法pop_heap,push_back,pop_back等等。

二、代码实现

sph算法代码GitHub链接

数据集链接

核心代码：

for (;;)
	{
		if (t > 0)
		{
			t = T;
			mind = 99999999;
			//所有点到目标点的距离
			for (int i = 1; i <= DD; i++)
			{
				if (s[i] == 1)
				{
					Dijkstra(i);
					//利用新的dist的数据对fdis的数据进行更新
					for (int j = 1; j <= DD; j++)
					{
						if (dist[j] < fdis[j] && dist[j] != 0 && s[j] != 1)
						{
							fdis[j] = dist[j];
							for (int k = 0; k <= DD; k++)
							{
								fload[j][k] = load[j][k];
								if (fload[j][k] == 0)
									break;
							}
						}
					}
				}
			}
			fdis[first] = 0;
			//找出最小的点（目标点中）
			for (int i = 1; i <= DD; i++)
			{
				for (int j = 0; j < T; j++)
				{
					if (mind > fdis[i] && i == goal[j] && goal2[i] != 1)//这点距离小，在目标点中间，且未进入点集s
					{
						mind = fdis[i];
						minv = i;
					}
				}
			}
			//找出的点加入点集s
			goal2[minv] = 1;
			for (int i = 0; i <= DD; i++)
			{
				if (fload[minv][i] > 0)
					s[fload[minv][i]] = 1;
				else
					break;
			}
			for (int i = 1; i <= DD; i++)
			{
				if (1 == goal2[i])
					t--;
			}
		}
		else
			break;
	}

贴几个跑完的数据。

• 数据1：
  
  first：2
  
  目标点1、2、3、4、5、6、7、8、9、10
  
  点集图：
  
  

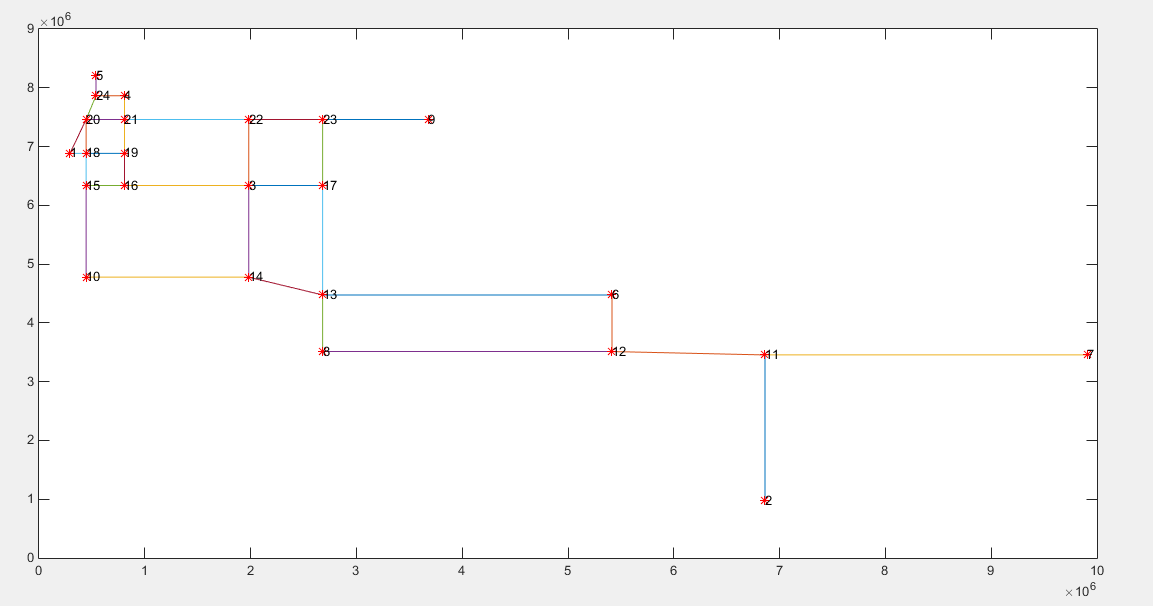
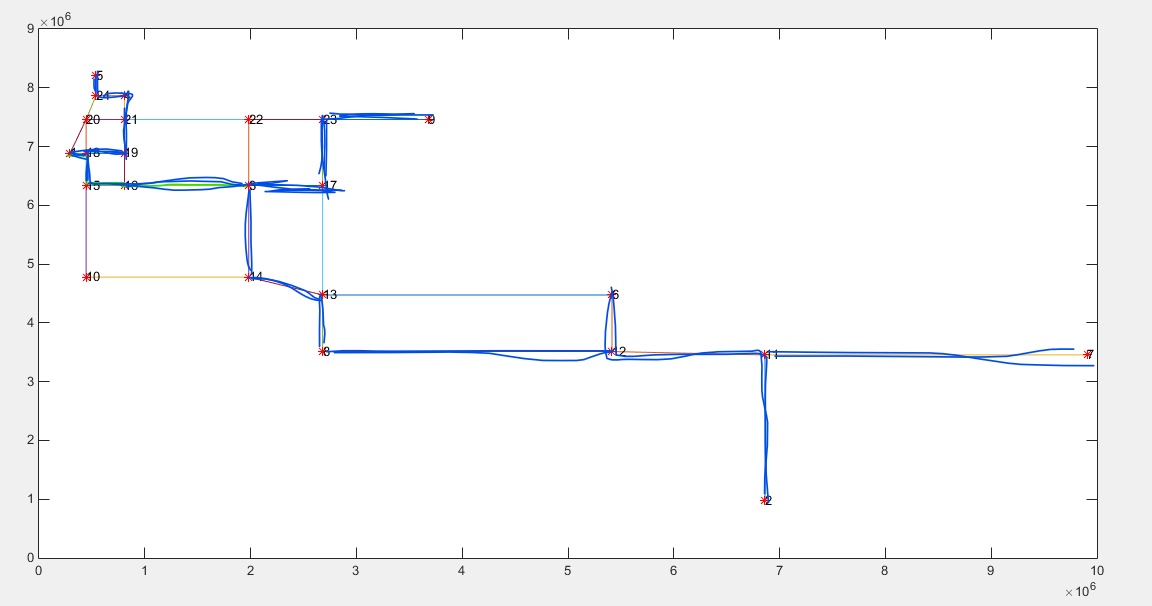
路径图：（别吐槽。。。matlab用的烂，有空补不是手绘的。。。）

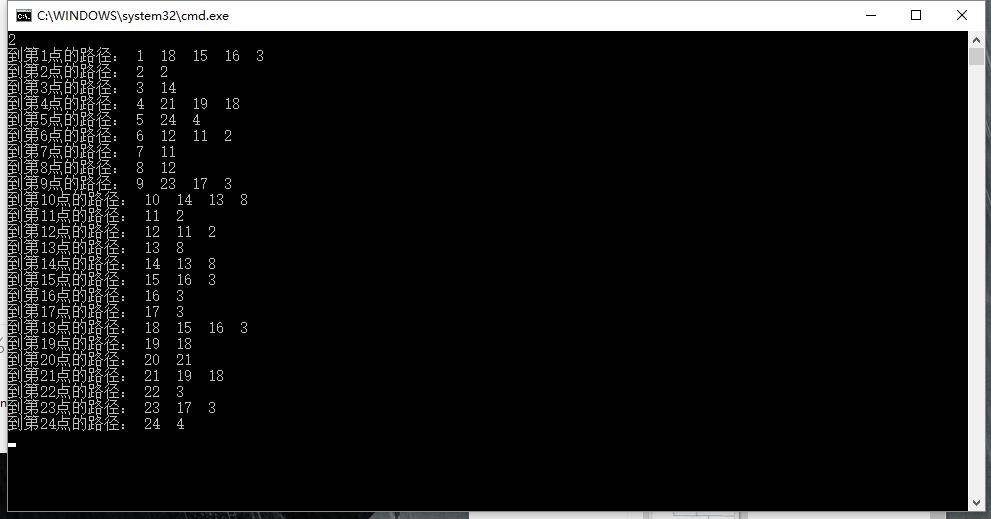
程序结果截图：

• 数据2：
  
  first：1
  
  目标点1、2、3、4、5、6、7、8、9、10
  
  点集图：
  
  

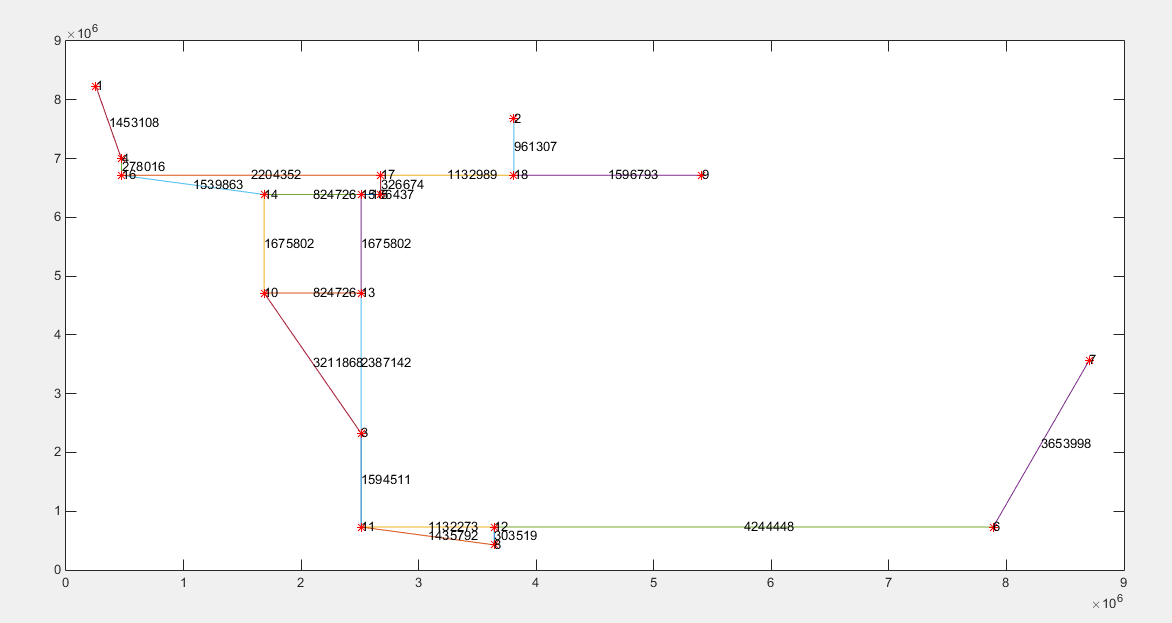
路径图：

程序结果截图：

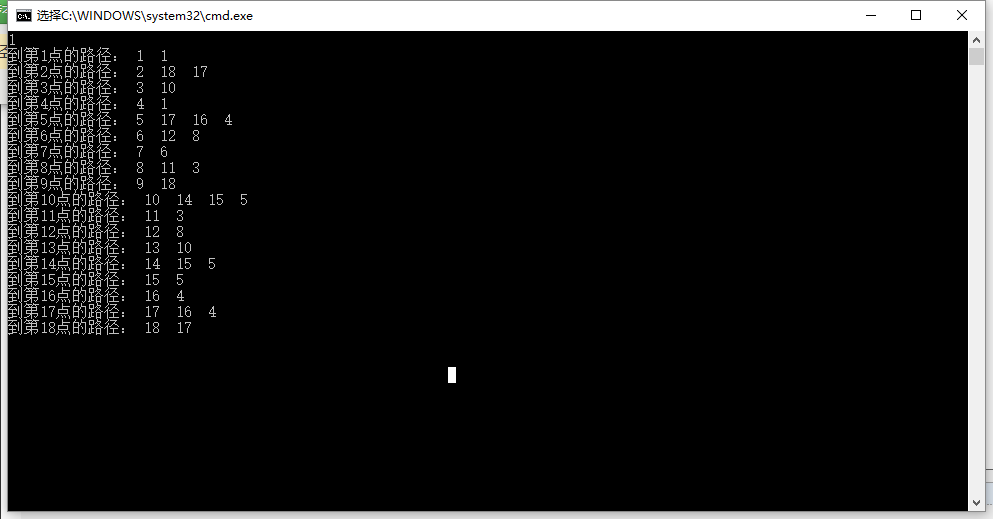
-数据3：

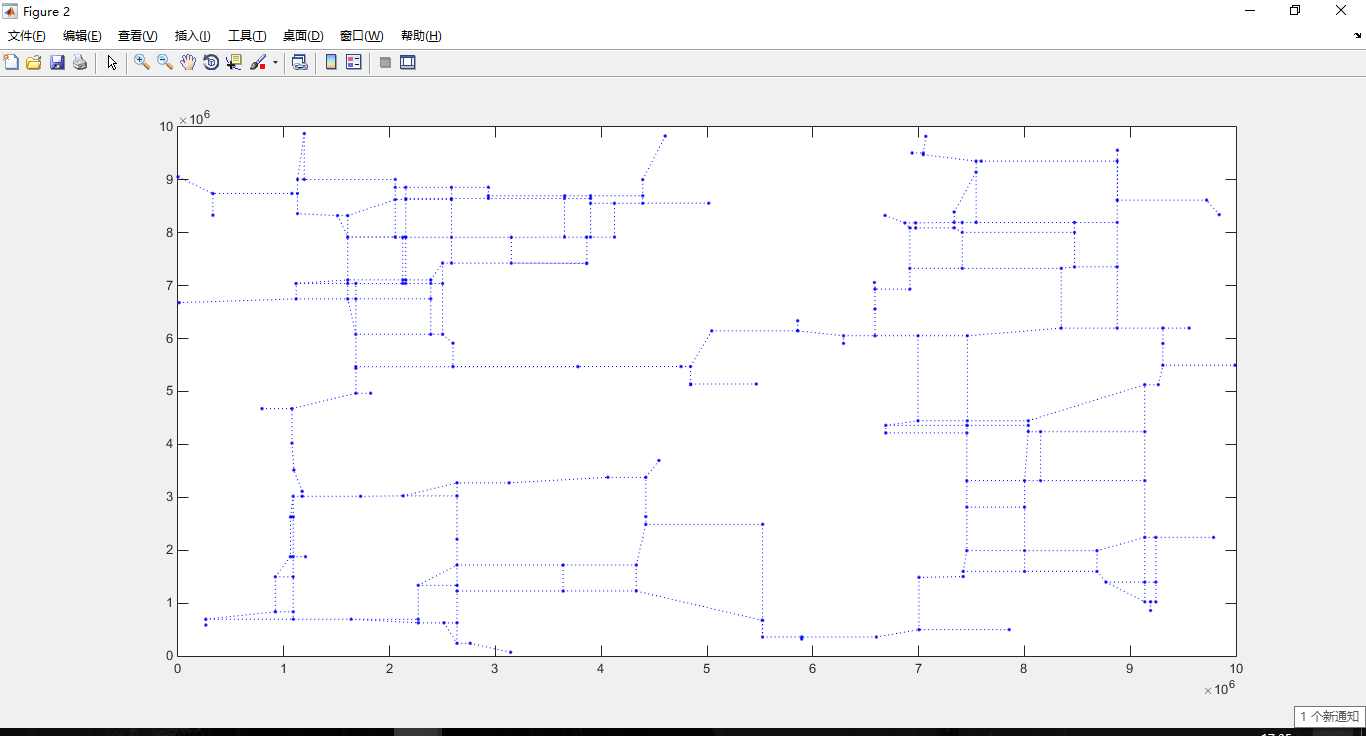
点集图：

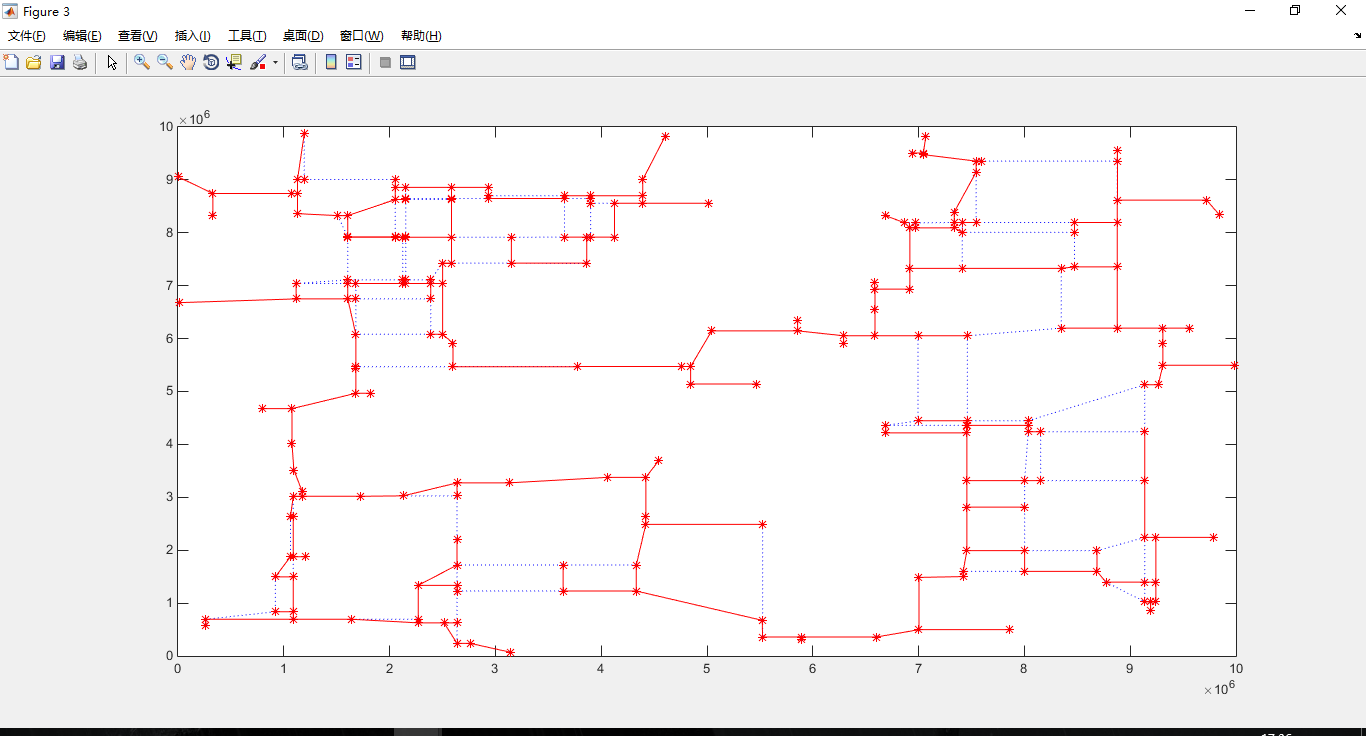
路径图：

emmmmm........就是这样，学习中大佬们指教。